目录

1. 矩阵中的最长递增路径  🌟🌟🌟

2. 编辑距离  🌟🌟🌟

3. 数据流的中位数  🌟🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

---

1. 矩阵中的最长递增路径

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

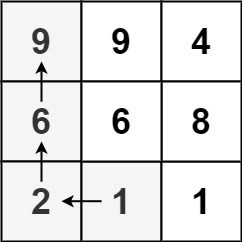
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 2^31 - 1

出处：

https://edu.csdn.net/practice/27049323

代码：

import java.util.*;
class longestIncreasingPath {
    public static class Solution {
        public int longestIncreasingPath(int[][] matrix) {
            if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
                return 0;
            }
            int max = 0;
            int row = matrix.length;
            int col = matrix[0].length;
            int[][] dp = new int[row][col];
            for (int i = 0; i < row; i++) {
                for (int j = 0; j < col; j++) {
                    max = Math.max(max, loop(matrix, Integer.MIN_VALUE, dp, i, j));
                }
            }
            return max;
        }
        private int loop(int[][] mat, int pre, int[][] dp, int i, int j) {
            if (i < 0 || j < 0 || i >= mat.length || j >= mat[0].length || mat[i][j] <= pre) {
                return 0;
            }
            if (dp[i][j] != 0) {
                return dp[i][j];
            }
            int max = 0;
            max = Math.max(max, loop(mat, mat[i][j], dp, i - 1, j));
            max = Math.max(max, loop(mat, mat[i][j], dp, i + 1, j));
            max = Math.max(max, loop(mat, mat[i][j], dp, i, j - 1));
            max = Math.max(max, loop(mat, mat[i][j], dp, i, j + 1));
            dp[i][j] = max + 1;
            return dp[i][j];
        }
    }
    public static void main(String[] args) {
        Solution obj = new Solution();
        int[][] matrix = {{9,9,4},{6,6,8},{2,1,1}};
        System.out.println(obj.longestIncreasingPath(matrix));
        int[][] matrix2 = {{3,4,5},{3,2,6},{2,2,1}};
        System.out.println(obj.longestIncreasingPath(matrix2));
   }
}

输出：

4
4

---

2. 编辑距离

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：horse -> rorse (将 'h' 替换为 'r')rorse -> rose (删除 'r')rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：intention -> inention (删除 't')inention -> enention (将 'i' 替换为 'e')enention -> exention (将 'n' 替换为 'x')exention -> exection (将 'n' 替换为 'c')exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

以下程序实现了这一功能，请你填补空白处内容：

```Java
class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        if (len1 * len2 == 0)
            return len1 + len2;
        String longerStr = len1 > len2 ? word1 : word2;
        String shorterStr = len1 > len2 ? word2 : word1;
        int shorterOne = Math.min(len1, len2);
        int[] dp = new int[shorterOne + 1];
        for (int i = 0; i < shorterOne + 1; i++) {
            dp[i] = i;
        }
        for (int j = 1; j <= longerStr.length(); j++) {
            int left = j;
            for (int i = 1; i <= shorterStr.length(); i++) {
                int updateDown = dp[i] + 1;
                int updateLeft = left + 1;
                int updateLeftDown = dp[i - 1];
                if (longerStr.charAt(j - 1) != shorterStr.charAt(i - 1)) {
                    updateLeftDown++;
                }
                int min = Math.min(updateLeft, Math.min(updateDown, updateLeftDown));
                dp[i - 1] = left;
                _____________________;
            }
        }
        return dp[shorterOne];
    }
}
```

出处：

https://edu.csdn.net/practice/27049324

代码：

import java.util.*;
class minDistance {
    public static class Solution {
        public int minDistance(String word1, String word2) {
            int len1 = word1.length();
            int len2 = word2.length();
            if (len1 * len2 == 0)
                return len1 + len2;
            String longerStr = len1 > len2 ? word1 : word2;
            String shorterStr = len1 > len2 ? word2 : word1;
            int shorterOne = Math.min(len1, len2);
            int[] dp = new int[shorterOne + 1];
            for (int i = 0; i < shorterOne + 1; i++) {
                dp[i] = i;
            }
            for (int j = 1; j <= longerStr.length(); j++) {
                int left = j;
                for (int i = 1; i <= shorterStr.length(); i++) {
                    int updateDown = dp[i] + 1;
                    int updateLeft = left + 1;
                    int updateLeftDown = dp[i - 1];
                    if (longerStr.charAt(j - 1) != shorterStr.charAt(i - 1)) {
                        updateLeftDown++;
                    }
                    int min = Math.min(updateLeft, Math.min(updateDown, updateLeftDown));
                    dp[i - 1] = left;
                    if (i == dp.length - 1) {
                        dp[i] = min;
                    } else {
                        left = min;
                    }
                }
            }
            return dp[shorterOne];
        }
    }
    public static void main(String[] args) {
        Solution obj = new Solution();
        String word1 = "horse";
        String word2 = "ros";
        System.out.println(obj.minDistance(word1, word2));
        word1 = "intention";
        word2 = "execution";
        System.out.println(obj.minDistance(word1, word2));
   }
}

输出：

3
5

---

3. 数据流的中位数

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。
• double findMedian() - 返回目前所有元素的中位数。

示例：

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2

进阶:

1. 如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？
2. 如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

出处：

https://edu.csdn.net/practice/27049325

代码：

import java.util.*;
class MedianFinder {
    PriorityQueue<Integer> min;
    PriorityQueue<Integer> max;
    /** initialize your data structure here. */
    public MedianFinder() {
        min = new PriorityQueue<>();
        max = new PriorityQueue<>((a, b) -> {
            return b - a;
        });
    }
    public void addNum(int num) {
        max.add(num);
        min.add(max.remove());
        if (min.size() > max.size())
            max.add(min.remove());
    }
    public double findMedian() {
        if (max.size() == min.size())
            return (max.peek() + min.peek()) / 2.0;
        else
            return max.peek();
    }
    public static void main(String[] args) {
        MedianFinder obj = new MedianFinder();
        obj.addNum(1);
        obj.addNum(2);
        System.out.println(obj.findMedian());
        obj.addNum(3);
        System.out.println(obj.findMedian());
   }
}
/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

输出：

1.5
2.0

---

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.csdn.net/ 

	Golang每日一练 专栏
	Python每日一练 专栏
	C/C++每日一练 专栏
	Java每日一练 专栏