创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!!
主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步!
给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ
c语言系列专栏: c语言之路重点知识整合
目录
一、递归基本概念的理解
二、递归算法的基本模式
一些习题实例:
两个正整数的最大公约数
用递归算法实现斐波那契数列
一、递归基本概念的理解
函数递归就是函数在其内部再次调用自己的过程。
递归是一种解决问题的方法,它将问题分解成更小的子问题,直到这些子问题的解决方法变得简单明了。在递归过程中,当执行到一个终止条件时,递归过程就会结束,返回结果给上一级递归函数,并依次返回给最初调用的函数。
递归算法在解决一些实际问题时会更简单明了
二、递归算法的基本模式
递归算法的基本模式:终止条件,递推公式
例如: 计算阶乘5*4*3*2*1=
#include <stdio.h>
int fun01(int n);
int main()
{
printf("%d\n",fun01(5));
return 0;
}
int fun01(int n)
{
if (n==1) //终止条件
{
return 1;
}
return n*fun01(n-1); //递推公式
}阶乘计算到1,终止条件为n==1
阶乘计算为前一个数累乘到后一个数,递推公式为 n*fun01(n-1)
一定要有终止条件!!因为没有终止条件会一直循环,过度递归可能会导致栈溢出。
一些习题实例:
两个正整数的最大公约数
不断向下取余,直到取尽
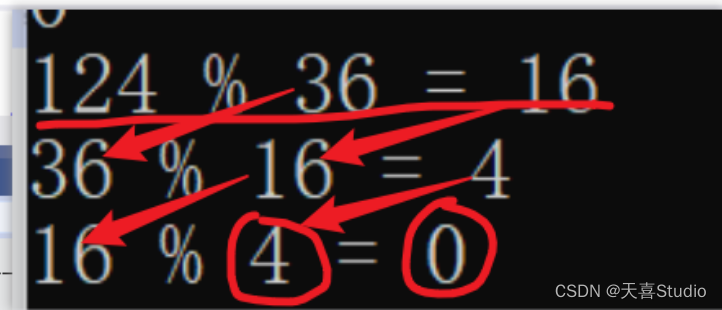
#include <stdio.h>
int fun11(int m,int n);
int main()
{
/* 递归实现:两个正整数的最大公约数 */
printf("%d\n",fun11(124,36));
return 0;
}
int fun11(int m,int n)
{
if (m % n == 0)
{
return n;
}
return fun11(n, m % n);
}使用调试器查看:
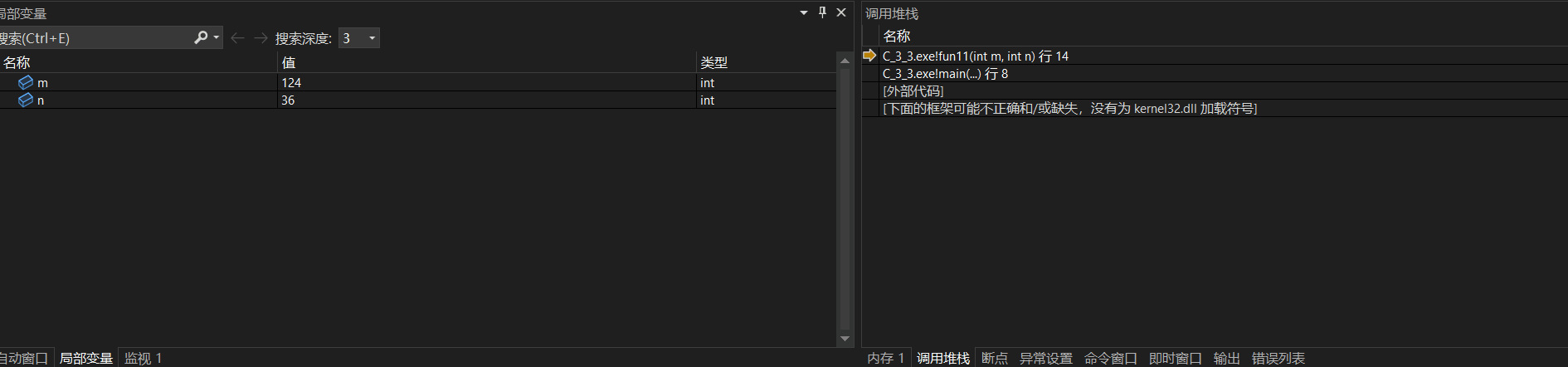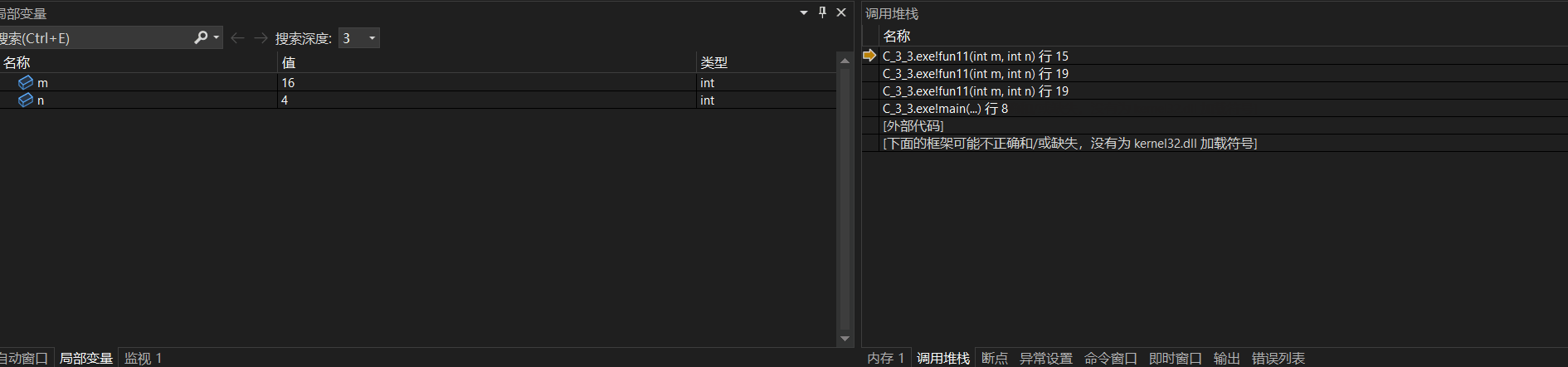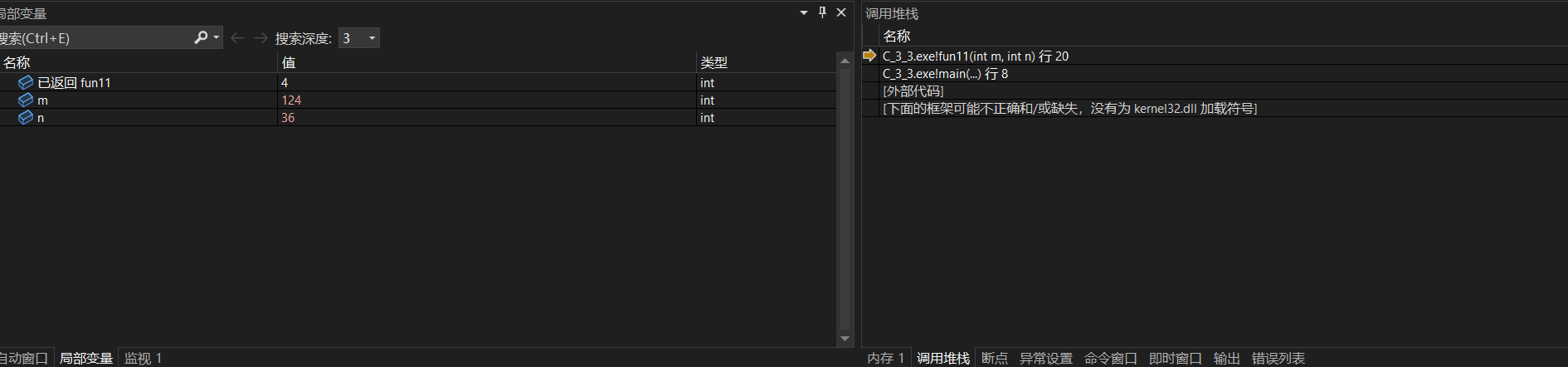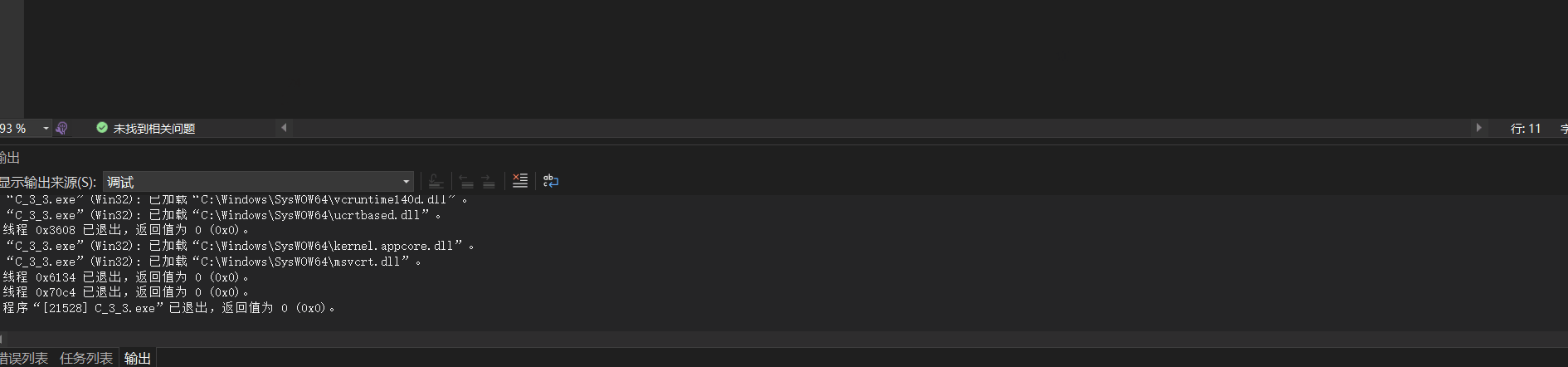
最终返回结果为4
用递归算法实现斐波那契数列
后一项等于前两项之和,直到开头两项为止
#include <stdio.h>
int fun13(int n);
int main()
{
/*用递归算法实现斐波那契数列: */
int i;
for(i=1;i<=20;i++)
{
printf("%d,",fun13(i));
}
return 0;
}
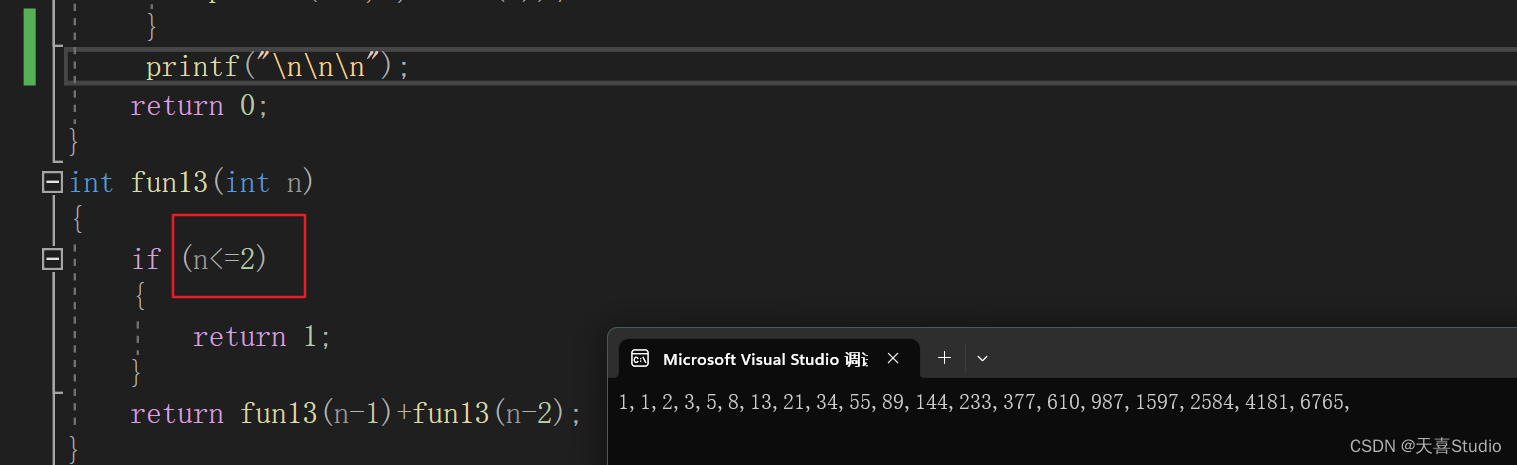
int fun13(int n)
{
if (n<=2)
{
return 1;
}
return fun13(n-1)+fun13(n-2);
}