[LeetCode周赛复盘] 第 343 场周赛20230430
- 一、本周周赛总结
- 2660. 保龄球游戏的获胜者
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2661. 找出叠涂元素
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2662. 前往目标的最小代价
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2663. 字典序最小的美丽字符串
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- T1 模拟。
- T2 网格图计数。
- T3 最短路。
- T4 贪心构造。
2660. 保龄球游戏的获胜者
2660. 保龄球游戏的获胜者
1. 题目描述
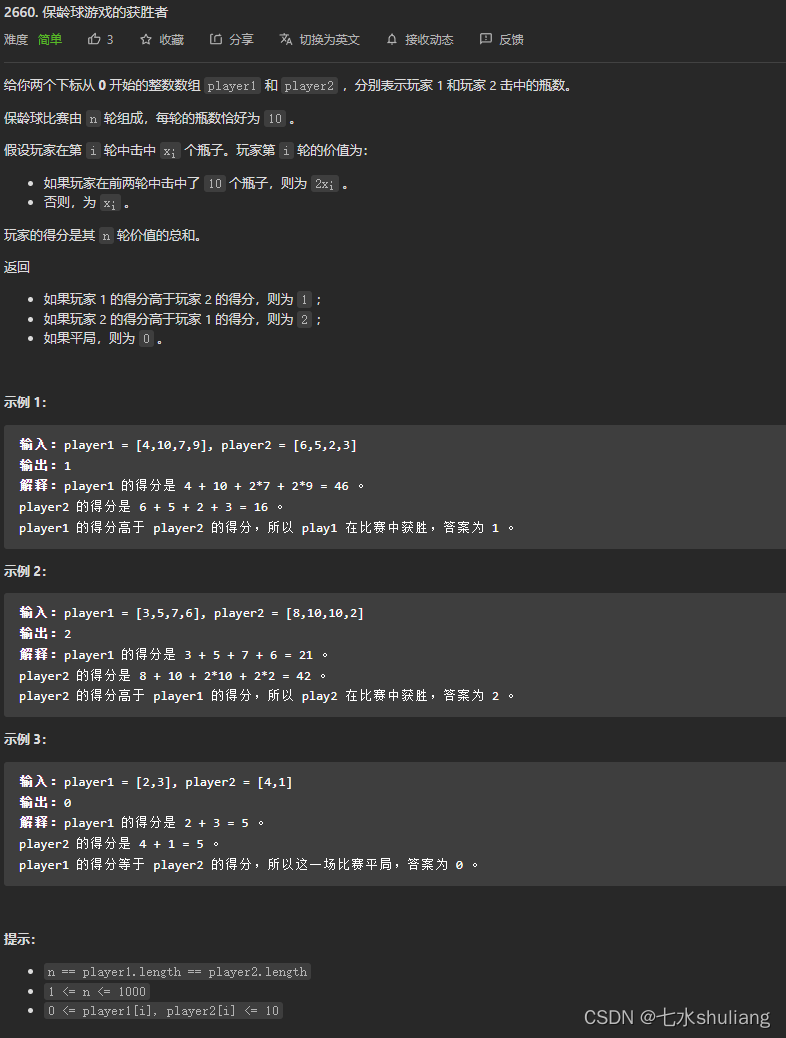
2. 思路分析
- 题意描述有误,建议翻看英文题面。
- 实际第一条规则为:若第i-1或i-2轮有10瓶,则第i轮得分翻倍。
3. 代码实现
def calc(a):
ans = 0
for i,v in enumerate(a):
if i and a[i-1] == 10 or i-1>0 and a[i-2] == 10:
v *= 2
ans += v
return ans
class Solution:
def isWinner(self, p1: List[int], p2: List[int]) -> int:
a,b = calc(p1),calc(p2)
if a == b:
return 0
if a > b:
return 1
return 2
2661. 找出叠涂元素
2661. 找出叠涂元素
1. 题目描述

2. 思路分析
- 题面不太清楚,实际是按arr元素顺序染色mat,问最早什么时刻能让某一列或行涂满。其中时刻用arr中的下标表示。
- 那么可以每行/每列计数,当这行/列填满时,计数为n/m。
- 我在实现时用了减法。
3. 代码实现
class Solution:
def firstCompleteIndex(self, arr: List[int], mat: List[List[int]]) -> int:
m,n = len(mat),len(mat[0])
p = {}
for i,row in enumerate(mat):
for j,v in enumerate(row):
p[v] = (i,j)
rows = [n]*m
cols = [m] * n
for i,v in enumerate(arr):
x,y = p[v]
rows[x] -= 1
cols[y] -= 1
if not rows[x] or not cols[y]:
return i
2662. 前往目标的最小代价
2662. 前往目标的最小代价
1. 题目描述
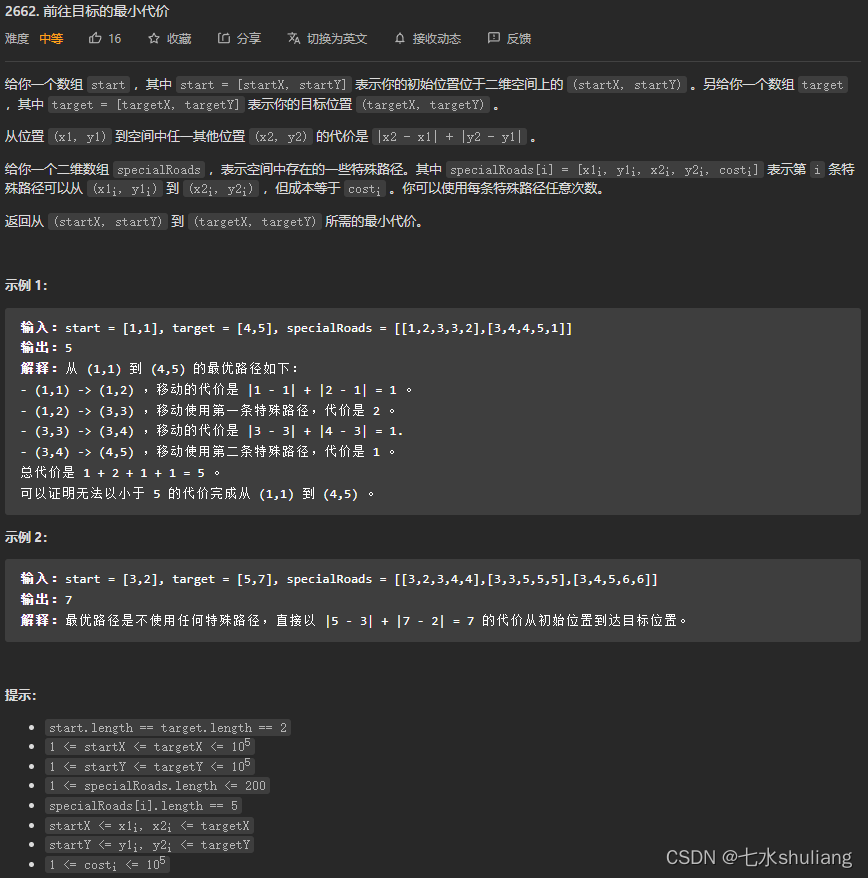
2. 思路分析
- 最差的方案就是从start直接走曼哈顿距离到target。
- 这题主要是建图,给出的捷径肯定要建图。另外若可以走多个结晶,显然是首尾相接。
- 省事的方案就是直接把所有涉及的点都互相连接即可。稠密图。
- 然后跑Dijkstra,注意这里的点是离散的,因此可以用defaultdict搞。而且由于是二维坐标,可以直接压缩成一个int64。
- 另外由于是稠密图,可以不建图,跑朴素n方dij。每次转移遍历所有已处理的最短路,找最短的点扩展,这样可以直接计算到所有为止的曼哈顿距离,省去建图。
3. 代码实现
class Solution:
def minimumCost(self, start: List[int], target: List[int], specialRoads: List[List[int]]) -> int:
g = defaultdict(dict)
def get(x,y):
return x * 1000000+y
def add_edge(u,v,w):
if v in g[u]:
g[u][v] = min(g[u][v],w)
else:
g[u][v] = w
def manhadun(x1,y1,x2,y2):
return abs(x1-x2) + abs(y1-y2)
sx,sy = start
tx,ty = target
s,t = get(sx,sy),get(tx,ty)
add_edge(s,t,manhadun(tx,ty,sx,sy))
ps = {(sx,sy),(tx,ty)}
def add_p(x,y):
ps.add((x,y))
for x1,y1,x2,y2,w in specialRoads:
add_p(x1,y1)
add_p(x2,y2)
u,v = get(x1,y1),get(x2,y2)
add_edge(u,v,w)
add_edge(s,u,manhadun(sx,sy,x1,y1))
add_edge(v,t,manhadun(x2,y2,tx,ty))
for x1,y1 in ps:
u = get(x1,y1)
for x2,y2 in ps:
v = get(x2,y2)
add_edge(u,v,manhadun(x2,y2,x1,y1))
dis = defaultdict(lambda : inf)
q = [(0,s)]
while q:
c,u = heappop(q)
if u == t :
return c
if c > dis[u]:continue
for v, w in g[u].items():
d = c + w
if d < dis[v]:
dis[v] = d
heappush(q,(d,v))
return -1
2663. 字典序最小的美丽字符串
2663. 字典序最小的美丽字符串
1. 题目描述
2. 思路分析
贪心
- 由于是要最小的字典序,那么一定是从后边开始修改(increase)。
- 注意s本身是美丽字符串。挖掘一下性质。
- 所有长为m回文串可以删除两边的串,剩下长度为m-2的串,且剩余串也必是回文串。
- 逆否命题为,若中间的子串不回文,原串也必不是回文。
- 那么本题其实就是要求没有长度为2或者3的回文串。
- 注意,输入的s已经满足这个性质。
- 先把s[n-1]++,令i=n-1然后判断:
- 若s[i]>k,即越界,则需要进位,令s[i]=‘a’,s[i-1]++;这里注意若i==0,则非法。
- 若s[i]和s[i-1]/s[i-2]冲突,则s[i]需要继续++,直到不冲突。
- 在这之前,需要先处理s[i-1],若s[i-1]由于i的修改,变得越界或冲突,需要先处理。
- 那么i-1可能还会修改i-2,优先处理。这是个递归/循环的过程。
- 在这之前,需要先处理s[i-1],若s[i-1]由于i的修改,变得越界或冲突,需要先处理。
- 当“递”处理到左边某一个位置时,它不再进位或冲突,则不用继续向左探测了,可以向右“归”。
- 由于k>=4,向右归时若冲突,顶多进到’c’(因为是从’a’开始)。
- 整个过程是一个先向左再向右的过程。
- 具体看代码。
- 注意为什么先处理左边在处理右边,可能的疑问:若先处理左边,右边岂不是可以变小?
- 实际上,i-1只会因为i的进位而增加,这时i已经是a了,没得减小。
3. 代码实现
class Solution:
def smallestBeautifulString(self, s: str, k: int) -> str:
n = len(s)
s = list(s)
ans = list(s)
up = chr(ord('a') + k - 1)
i = n - 1
ans[n-1] = chr(ord(ans[i]) + 1)
while i < n:
if ans[i] > up:
if i == 0 :
return ''
ans[i] = 'a'
i -= 1
ans[i] = chr(ord(ans[i]) + 1)
elif i and ans[i] == ans[i-1] or i-1>0 and ans[i] == ans[i-2]:
ans[i] = chr(ord(ans[i]) + 1)
else:
i += 1
return ''.join(ans)