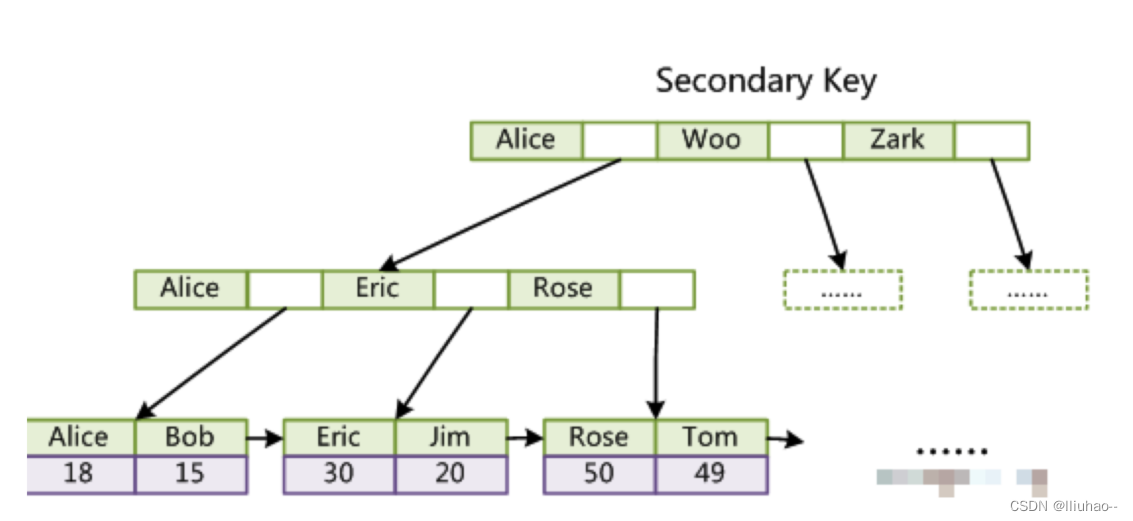
线段树详解：https://leetcode.cn/problems/range-module/solution/by-lfool-eo50/

文章目录

线段树
- 线段树模板
- [729. 我的日程安排表 I](https://leetcode.cn/problems/my-calendar-i/)
- [731. 我的日程安排表 II](https://leetcode.cn/problems/my-calendar-ii/)
- [732. 我的日程安排表 III](https://leetcode.cn/problems/my-calendar-iii/)
- 🔺[715. Range 模块](https://leetcode.cn/problems/range-module/)
- [307. 区域和检索 - 数组可修改](https://leetcode.cn/problems/range-sum-query-mutable/)
- [933. 最近的请求次数](https://leetcode.cn/problems/number-of-recent-calls/)
- [2407. 最长递增子序列 II](https://leetcode.cn/problems/longest-increasing-subsequence-ii/)
- [933. 最近的请求次数](https://leetcode.cn/problems/number-of-recent-calls/)
- [699. 掉落的方块](https://leetcode.cn/problems/falling-squares/)

线段树

729. 我的日程安排表 I

731. 我的日程安排表 II

732. 我的日程安排表 III

715. Range 模块

307. 区域和检索 - 数组可修改

933. 最近的请求次数

699. 掉落的方块

2407. 最长递增子序列 II

线段树模板

模板：注意：下面模版基于求「区间和」以及对区间进行「加减」的更新操作，且为「动态开点」

public class SegmentTreeDynamic {
    class Node {
        Node left, right;
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
	//初始值start和end是固定的0-N，l和r是要更新的区间，更新值为val
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val += (end - start + 1) * val;
            node.add += val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
	
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
	
    private void pushUp(Node node) {
        node.val = node.left.val + node.right.val;
    }
	
    private void pushDown(Node node, int leftNum, int rightNum) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add * leftNum;
        node.right.val += node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
    
}

729. 我的日程安排表 I

难度中等256

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的日程安排不会造成 重复预订 ，则可以存储这个新的日程安排。

当两个日程安排有一些时间上的交叉时（例如两个日程安排都在同一时间内），就会产生 重复预订 。

日程可以用一对整数 start 和 end 表示，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end 。

实现 MyCalendar 类：

MyCalendar() 初始化日历对象。
boolean book(int start, int end) 如果可以将日程安排成功添加到日历中而不会导致重复预订，返回 true 。否则，返回 false 并且不要将该日程安排添加到日历中。

示例：

输入：
["MyCalendar", "book", "book", "book"]
[[], [10, 20], [15, 25], [20, 30]]
输出：
[null, true, false, true]

解释：
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False ，这个日程安排不能添加到日历中，因为时间 15 已经被另一个日程安排预订了。
myCalendar.book(20, 30); // return True ，这个日程安排可以添加到日历中，因为第一个日程安排预订的每个时间都小于 20 ，且不包含时间 20 。

提示：

0 <= start < end <= 109
每个测试用例，调用 book 方法的次数最多不超过 1000 次。

题解：问题是查看区间是否被占用，等同于查看区间最值，如果被占用了，则区间最大值为1，为0即表示区间没有被占用。每次book的时候设置区间值都为1

class MyCalendar {

    public MyCalendar() {

    }
    
    public boolean book(int start, int end) {
        int exist = query(root, 0, N, start, end-1);
        if(exist == 1) return false;
        update(root, 0, N, start, end-1, 1);
        return true;
    }

    class Node{
        Node left, right;
        int val, add;
    }
    private int N = (int)1e9;
    private Node root = new Node();

    public void update(Node node, int start, int end, int l, int r, int val){
        if(l <= start && r >= end){
            node.val = val;
            node.add = val;
            return; 
        }
        int mid = (start + end) >> 1;
        pushDown(node);
        if(l <= mid) update(node.left, start, mid, l, r, val);
        if(r > mid) update(node.right, mid+1, end, l, r, val);
        pushUp(node);
    }

    public int query(Node node, int start, int end, int l, int r){
        if(l <= start && r >= end){
            return node.val;
        }
        int mid = (start + end) >> 1;
        pushDown(node);
        int ans = 0;
        if(l <= mid) ans = Math.max(ans, query(node.left, start, mid, l, r));
        if(r > mid) ans = Math.max(ans, query(node.right, mid+1, end, l, r));
        return ans;
    }

    public void pushDown(Node node){
        if(node.left == null) node.left = new Node();
        if(node.right == null) node.right = new Node();
        if(node.add == 0) return;
        node.left.val = node.add;
        node.right.val = node.add;
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }

    public void pushUp(Node node){
        node.val = Math.max(node.left.val, node.right.val);
    }
}

731. 我的日程安排表 II

难度中等218

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内不会导致三重预订时，则可以存储这个新的日程安排。

MyCalendar 有一个 book(int start, int end)方法。它意味着在 start 到 end 时间内增加一个日程安排，注意，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end。

当三个日程安排有一些时间上的交叉时（例如三个日程安排都在同一时间内），就会产生三重预订。

每次调用 MyCalendar.book方法时，如果可以将日程安排成功添加到日历中而不会导致三重预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

请按照以下步骤调用MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)

示例：

MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(50, 60); // returns true
MyCalendar.book(10, 40); // returns true
MyCalendar.book(5, 15); // returns false
MyCalendar.book(5, 10); // returns true
MyCalendar.book(25, 55); // returns true
解释： 
前两个日程安排可以添加至日历中。 第三个日程安排会导致双重预订，但可以添加至日历中。
第四个日程安排活动（5,15）不能添加至日历中，因为它会导致三重预订。
第五个日程安排（5,10）可以添加至日历中，因为它未使用已经双重预订的时间10。
第六个日程安排（25,55）可以添加至日历中，因为时间 [25,40] 将和第三个日程安排双重预订；
时间 [40,50] 将单独预订，时间 [50,55）将和第二个日程安排双重预订。

提示：

每个测试用例，调用 MyCalendar.book 函数最多不超过 1000次。
调用函数 MyCalendar.book(start, end)时， start 和 end 的取值范围为 [0, 10^9]。

题解：问题同日程安排表1，区间最值 < 2

class MyCalendarTwo {

    public MyCalendarTwo() {
    }
    
    public boolean book(int start, int end) {
        // 不会导致三重预定，也就是区间最多update2次，query < 2
        if(query(root, 0, N, start, end-1) < 2){
            update(root, 0, N, start, end-1, 1);
            return true;
        }else{
            return false;
        }
    }

    class Node{
        Node left, right;
        int val, add;
    }

    private int N = (int)1e9;
    private Node root = new Node();

    public void update(Node node, int start, int end, int l, int r, int val){
        if(l <= start && r >= end){
            node.val += val;
            node.add += val;
            return;
        }
        int mid = (start + end) >> 1;
        pushDown(node);
        if(l <= mid) update(node.left, start, mid, l, r, val);
        if(r > mid) update(node.right, mid+1, end, l, r, val);
        pushUp(node); 
    }

    public int query(Node node, int start, int end, int l, int r){
        if(l <= start && r >= end){
            return node.val;
        }
        int mid = (start + end) >> 1;
        pushDown(node);
        int res = 0;
        if(l <= mid) res = Math.max(res, query(node.left, start, mid, l, r));
        if(r > mid) res = Math.max(res, query(node.right, mid+1, end, l, r));
        return res;
    }

    public void pushDown(Node node){
        if(node.left == null) node.left = new Node();
        if(node.right == null) node.right = new Node();
        if(node.add == 0) return;
        node.left.val += node.add;
        node.right.val += node.add;
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }

    public void pushUp(Node node){
        node.val = Math.max(node.left.val, node.right.val);
    }
}

732. 我的日程安排表 III

难度困难203

当 k 个日程安排有一些时间上的交叉时（例如 k 个日程安排都在同一时间内），就会产生 k 次预订。

给你一些日程安排 [start, end) ，请你在每个日程安排添加后，返回一个整数 k ，表示所有先前日程安排会产生的最大 k 次预订。

实现一个 MyCalendarThree 类来存放你的日程安排，你可以一直添加新的日程安排。

MyCalendarThree() 初始化对象。
int book(int start, int end) 返回一个整数 k ，表示日历中存在的 k 次预订的最大值。

示例：

输入：
["MyCalendarThree", "book", "book", "book", "book", "book", "book"]
[[], [10, 20], [50, 60], [10, 40], [5, 15], [5, 10], [25, 55]]
输出：
[null, 1, 1, 2, 3, 3, 3]

解释：
MyCalendarThree myCalendarThree = new MyCalendarThree();
myCalendarThree.book(10, 20); // 返回 1 ，第一个日程安排可以预订并且不存在相交，所以最大 k 次预订是 1 次预订。
myCalendarThree.book(50, 60); // 返回 1 ，第二个日程安排可以预订并且不存在相交，所以最大 k 次预订是 1 次预订。
myCalendarThree.book(10, 40); // 返回 2 ，第三个日程安排 [10, 40) 与第一个日程安排相交，所以最大 k 次预订是 2 次预订。
myCalendarThree.book(5, 15); // 返回 3 ，剩下的日程安排的最大 k 次预订是 3 次预订。
myCalendarThree.book(5, 10); // 返回 3
myCalendarThree.book(25, 55); // 返回 3

提示：

0 <= start < end <= 109
每个测试用例，调用 book 函数最多不超过 400次

题解：同日程安排表Ⅱ，返回最大值（统计区间最值，对区间进行加减操作）

class MyCalendarThree {

    public MyCalendarThree() {

    }
    
    public int book(int startTime, int endTime) {
        update(root, 0, N, startTime, endTime-1, 1);
        return query(root, 0, N, 0, N);
    }

    class Node{
        Node left, right;
        int val, add;
    }

    private int N = (int)1e9;
    private Node root = new Node();

    public void update(Node node, int start, int end, int l, int r, int val){
        if(l <= start && r >= end){
            node.val += val;
            node.add += val;
            return;
        }
        int mid = (start + end) >> 1;
        pushDown(node);
        if(l <= mid) update(node.left, start, mid, l, r, val);
        if(r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }

    public int query(Node node, int start, int end, int l, int r){
        if(l <= start && r >= end){
            return node.val;
        }
        int mid = (start + end) >> 1;
        pushDown(node);
        int res = 0;
        if(l <= mid) res = Math.max(res, query(node.left, start, mid, l, r));
        if(r > mid) res = Math.max(res, query(node.right, mid + 1, end, l, r));
        return res;
    }

    private void pushDown(Node node){
        if(node.left == null) node.left = new Node();
        if(node.right == null) node.right = new Node();
        if(node.add == 0) return;
        node.left.val += node.add;
        node.right.val += node.add;
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0; 
    }

    private void pushUp(Node node){
        node.val = Math.max(node.left.val, node.right.val);
    }

}

🔺715. Range 模块

难度困难216

Range模块是跟踪数字范围的模块。设计一个数据结构来跟踪表示为 半开区间 的范围并查询它们。

半开区间 [left, right) 表示所有 left <= x < right 的实数 x 。

实现 RangeModule 类:

RangeModule() 初始化数据结构的对象。
void addRange(int left, int right) 添加 半开区间 [left, right)，跟踪该区间中的每个实数。添加与当前跟踪的数字部分重叠的区间时，应当添加在区间 [left, right) 中尚未跟踪的任何数字到该区间中。
boolean queryRange(int left, int right) 只有在当前正在跟踪区间 [left, right) 中的每一个实数时，才返回 true ，否则返回 false 。
void removeRange(int left, int right) 停止跟踪 半开区间 [left, right) 中当前正在跟踪的每个实数。

示例 1：

输入
["RangeModule", "addRange", "removeRange", "queryRange", "queryRange", "queryRange"]
[[], [10, 20], [14, 16], [10, 14], [13, 15], [16, 17]]
输出
[null, null, null, true, false, true]

解释
RangeModule rangeModule = new RangeModule();
rangeModule.addRange(10, 20);
rangeModule.removeRange(14, 16);
rangeModule.queryRange(10, 14); 返回 true （区间 [10, 14) 中的每个数都正在被跟踪）
rangeModule.queryRange(13, 15); 返回 false（未跟踪区间 [13, 15) 中像 14, 14.03, 14.17 这样的数字）
rangeModule.queryRange(16, 17); 返回 true （尽管执行了删除操作，区间 [16, 17) 中的数字 16 仍然会被跟踪）

提示：

1 <= left < right <= 109
在单个测试用例中，对 addRange 、 queryRange 和 removeRange 的调用总数不超过 104 次

题解：每个节点的值表示当前区间是否被覆盖

class RangeModule {

    public RangeModule() {

    }
    
    public void addRange(int left, int right) {
        // 1 表示复盖；-1 表示取消覆盖
        update(root, 0, N, left, right-1, 1);
    }
    
    public boolean queryRange(int left, int right) {
        return query(root, 0, N, left, right-1);
    }
    
    public void removeRange(int left, int right) {
        update(root, 0, N, left, right-1, -1);
    }


    class Node{
        Node left, right;
        boolean cover; // 表示当前区间是否被覆盖
        int add;
    }

    private int N = (int)1e9;
    private Node root = new Node();

    public void update(Node node, int start, int end, int l, int r, int val){
        if(l <= start && r >= end){
            node.cover = val == 1;
            node.add = val;
            return;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if(l <= mid) update(node.left, start, mid, l, r, val);
        if(r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }

    public boolean query(Node node, int start, int end, int l, int r){
        if(l <= start && r >= end){
            return node.cover;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        // 查询左右子树是否被覆盖
        boolean res = true;
        if(l <= mid) res &= query(node.left, start, mid, l, r);
        if(r > mid) res &= query(node.right, mid + 1, end, l, r);
        return res;
    }

    private void pushDown(Node node,int leftNum, int rightNum){
        if(node.left == null) node.left = new Node();
        if(node.right == null) node.right = new Node();
        if(node.add == 0) return;
        node.left.cover = node.add == 1;
        node.right.cover = node.add == 1;
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0; 
    }

    private void pushUp(Node node){
        node.cover = node.left.cover && node.right.cover;
    }
}

307. 区域和检索 - 数组可修改

难度中等597

给你一个数组 nums ，请你完成两类查询。

其中一类查询要求更新数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（包含）的nums元素的和，其中 left <= right

实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值更新为 val
int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（包含）的nums元素的和（即，nums[left] + nums[left + 1], ..., nums[right]）

示例 1：

输入：
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 1 + 3 + 5 = 9
numArray.update(1, 2);   // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 1 + 2 + 5 = 8

提示：

1 <= nums.length <= 3 * 104
-100 <= nums[i] <= 100
0 <= index < nums.length
-100 <= val <= 100
0 <= left <= right < nums.length
调用 update 和 sumRange 方法次数不大于 3 * 104

class NumArray {

    public NumArray(int[] nums) {
        this.N = nums.length - 1;
        for(int i = 0; i <= N; i++){
            update(root, 0, N, i, i, nums[i]);
        }
    }
    
    public void update(int index, int val) {
        update(root, 0, N, index, index, val);
    }
    
    public int sumRange(int left, int right) {
        return query(root, 0, N, left, right);
    }

    class Node {
        Node left, right;
        int val, add;
    }
    private int N;
    private Node root = new Node();


	//初始值start和end是固定的0-N，l和r是要更新的区间，更新值为val
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val = (end - start + 1) * val;
            node.add = val;
            return;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
	
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
	
    private void pushUp(Node node) {
        node.val = node.left.val + node.right.val;
    }
	
    private void pushDown(Node node, int leftNum, int rightNum) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val = node.add * leftNum;
        node.right.val = node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(index,val);
 * int param_2 = obj.sumRange(left,right);
 */

933. 最近的请求次数

难度简单214

写一个 RecentCounter 类来计算特定时间范围内最近的请求。

请你实现 RecentCounter 类：

RecentCounter() 初始化计数器，请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求，其中 t 表示以毫秒为单位的某个时间，并返回过去 3000 毫秒内发生的所有请求数（包括新请求）。确切地说，返回在 [t-3000, t] 内发生的请求数。

保证每次对 ping 的调用都使用比之前更大的 t 值。

示例 1：

输入：
["RecentCounter", "ping", "ping", "ping", "ping"]
[[], [1], [100], [3001], [3002]]
输出：
[null, 1, 2, 3, 3]

解释：
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1);     // requests = [1]，范围是 [-2999,1]，返回 1
recentCounter.ping(100);   // requests = [1, 100]，范围是 [-2900,100]，返回 2
recentCounter.ping(3001);  // requests = [1, 100, 3001]，范围是 [1,3001]，返回 3
recentCounter.ping(3002);  // requests = [1, 100, 3001, 3002]，范围是 [2,3002]，返回 3

提示：

1 <= t <= 109
保证每次对 ping 调用所使用的 t 值都 严格递增
至多调用 ping 方法 104 次

2407. 最长递增子序列 II

难度困难60

给你一个整数数组 nums 和一个整数 k 。

找到 nums 中满足以下要求的最长子序列：

子序列 严格递增
子序列中相邻元素的差值 不超过 k 。

请你返回满足上述要求的 最长子序列 的长度。

子序列 是从一个数组中删除部分元素后，剩余元素不改变顺序得到的数组。

示例 1：

输入：nums = [4,2,1,4,3,4,5,8,15], k = 3
输出：5
解释：
满足要求的最长子序列是 [1,3,4,5,8] 。
子序列长度为 5 ，所以我们返回 5 。
注意子序列 [1,3,4,5,8,15] 不满足要求，因为 15 - 8 = 7 大于 3 。

示例 2：

输入：nums = [7,4,5,1,8,12,4,7], k = 5
输出：4
解释：
满足要求的最长子序列是 [4,5,8,12] 。
子序列长度为 4 ，所以我们返回 4 。

示例 3：

输入：nums = [1,5], k = 1
输出：1
解释：
满足要求的最长子序列是 [1] 。
子序列长度为 1 ，所以我们返回 1 。

提示：

1 <= nums.length <= 105
1 <= nums[i], k <= 105

线段树解法的最长递增子序列，状态从j-k < j' < j 而不是0 < j' < j转移过来

class Solution {	
    public int lengthOfLIS(int[] nums, int k) {
        for(int num : nums){
            num += (int)1e4; // -104 <= nums[i] <= 104，都变成正数
            int startidx = Math.max(num - k, 1);
            // 查找以元素值(1,num-1)结尾的LIS的最大值
            int res = 1 + query(root,1,N,startidx,num-1);
            update(root,1,N,num,num,res);// 更新为前面最大值 + 1
        }
        // 最后返回区间最大值
        return query(root,1,N,1,N);
    }

    class Node {
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val = val;
            node.add = val;
            return ;
        }
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
    private void pushUp(Node node) {
        // 每个节点存的是当前区间的最大值
        node.val = Math.max(node.left.val, node.right.val);
    }
    private void pushDown(Node node) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val = node.add;
        node.right.val = node.add;
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }
}

933. 最近的请求次数

难度简单214

写一个 RecentCounter 类来计算特定时间范围内最近的请求。

请你实现 RecentCounter 类：

RecentCounter() 初始化计数器，请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求，其中 t 表示以毫秒为单位的某个时间，并返回过去 3000 毫秒内发生的所有请求数（包括新请求）。确切地说，返回在 [t-3000, t] 内发生的请求数。

保证每次对 ping 的调用都使用比之前更大的 t 值。

示例 1：

输入：
["RecentCounter", "ping", "ping", "ping", "ping"]
[[], [1], [100], [3001], [3002]]
输出：
[null, 1, 2, 3, 3]

解释：
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1);     // requests = [1]，范围是 [-2999,1]，返回 1
recentCounter.ping(100);   // requests = [1, 100]，范围是 [-2900,100]，返回 2
recentCounter.ping(3001);  // requests = [1, 100, 3001]，范围是 [1,3001]，返回 3
recentCounter.ping(3002);  // requests = [1, 100, 3001, 3002]，范围是 [2,3002]，返回 3

提示：

1 <= t <= 109
保证每次对 ping 调用所使用的 t 值都 严格递增
至多调用 ping 方法 104 次

class RecentCounter {

    SegmentTreeDynamic t;

    public RecentCounter() {
        t = new SegmentTreeDynamic();
    }
    
    public int ping(int val) {
        t.update(t.root, 1, t.N, val, val, 1);
        return t.query(t.root, 1, t.N, Math.max(0, val - 3000), val);
    }
}

public class SegmentTreeDynamic {
    class Node {
        Node left, right;
        int val, add;
    }
    int N = (int) 1e9;
    Node root = new Node();
	//初始值start和end是固定的0-N，l和r是要更新的区间，更新值为val
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val += (end - start + 1) * val;
            node.add += val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
	
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
	
    private void pushUp(Node node) {
        node.val = node.left.val + node.right.val;
    }
	
    private void pushDown(Node node, int leftNum, int rightNum) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return;
        node.left.val += node.add * leftNum;
        node.right.val += node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
    
}

699. 掉落的方块

难度困难180

在二维平面上的 x 轴上，放置着一些方块。

给你一个二维整数数组 positions ，其中 positions[i] = [lefti, sideLengthi] 表示：第 i 个方块边长为 sideLengthi ，其左侧边与 x 轴上坐标点 lefti 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的 方块堆叠的最高高度 。

返回一个整数数组 ans ，其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。

示例 1：

输入：positions = [[1,2],[2,3],[6,1]]
输出：[2,5,5]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。
第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。
第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。
因此，返回 [2, 5, 5] 作为答案。

示例 2：

输入：positions = [[100,100],[200,100]]
输出：[100,100]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 100 。
第 2 个方块掉落后，最高的堆叠可以由方块 1 组成也可以由方块 2 组成，堆叠的最高高度为 100 。
因此，返回 [100, 100] 作为答案。
注意，方块 2 擦过方块 1 的右侧边，但不会算作在方块 1 上着陆。

提示：

1 <= positions.length <= 1000
1 <= lefti <= 108
1 <= sideLengthi <= 106

class Solution {
    public List<Integer> fallingSquares(int[][] positions) {
        // 求区间最值 区间加减操作
        List<Integer> res = new ArrayList<>();
        for(int[] p : positions){
            int left = p[0], right = p[0] + p[1], val = p[1];
            //先查询出 [x, x + h] 的值
            int cur = query(root, 0, N, left, right-1);
            //更新 [x, x + h - 1] 为 cur + h
            update(root, 0, N, left, right-1, val + cur);
            res.add(query(root, 0, N, 0, N));
        }
        //ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
        return res;
    }

    class Node {
        Node left, right;
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
	//初始值start和end是固定的0-N，l和r是要更新的区间，更新值为val
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val = val;
            node.add = val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
	
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans = Math.max(ans, query(node.left, start, mid, l, r));
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
	
    private void pushUp(Node node) {
        node.val = Math.max(node.left.val, node.right.val);
    }
	
    private void pushDown(Node node, int leftNum, int rightNum) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return;
        node.left.val = node.add;
        node.right.val = node.add;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }
}