分别利用seaborn和matplotlib绘制两组数据（国家统计局居民消费指数和鸢尾花数据集）的图表

news2024/11/23 7:08:40

一、居民消费指数

1. 数据来源

使用的数据来源网站：国家统计局
数据网站连接：https://data.stats.gov.cn/easyquery.htm?cn=A01
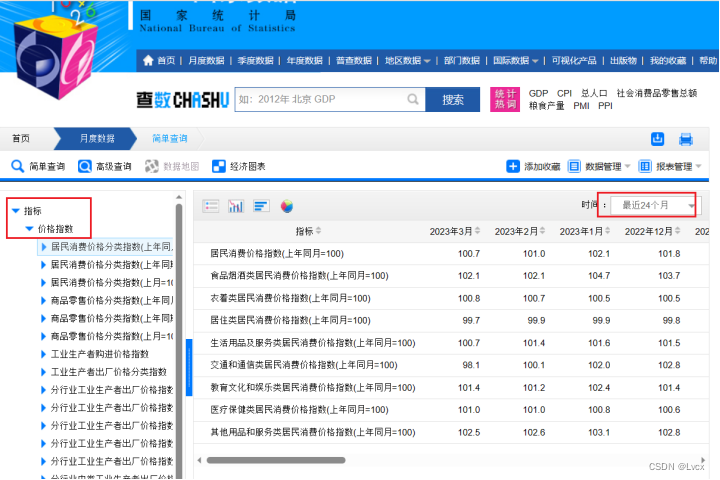
在这里插入图片描述

2.下载数据

点击下载按钮：
在这里插入图片描述

注册一个国家统计局的账号，然后自动登录跳转到数据页，再次点击下载，选择csv格式：
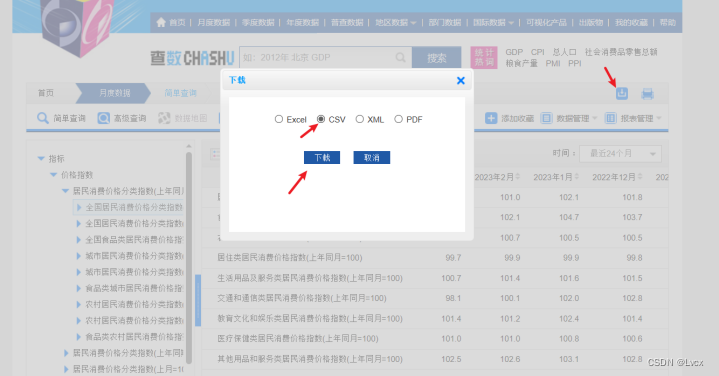
在这里插入图片描述

即可下载成功，在文件夹中打开：
在这里插入图片描述

打开文件我们即可看到数据：
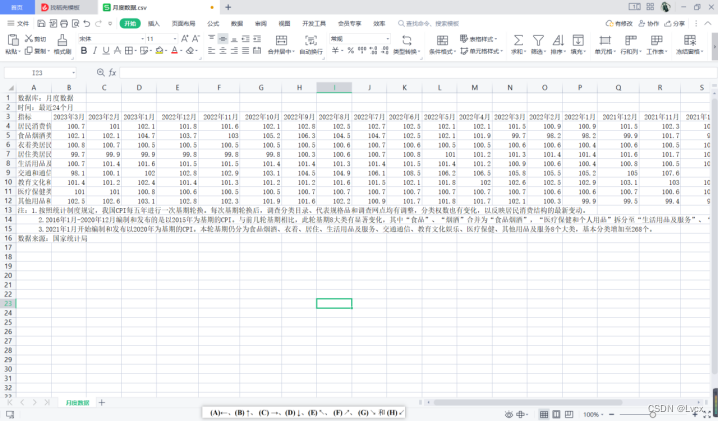
在这里插入图片描述

3. 调整数据

复制源数据的副本放在项目中，将不需要的数据删了（我们只保留2022年全年的数据）
在这里插入图片描述

4. 集中趋势分析：求均值、中位数、上四分位数、下四分位数

5. 计算极差、四分位差、方差、标准差、变异系数

6. 集中趋势分析、离散程度分析、分布形状分析

1.集中趋势分析
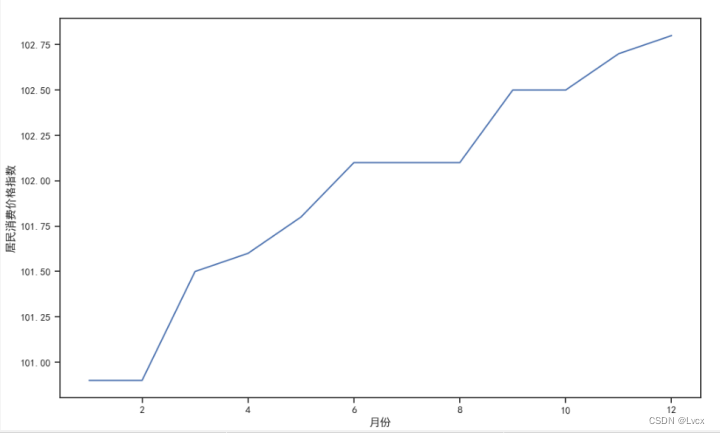
2022年全年的居民消费价格指数集中在100.9~102.8范围内，
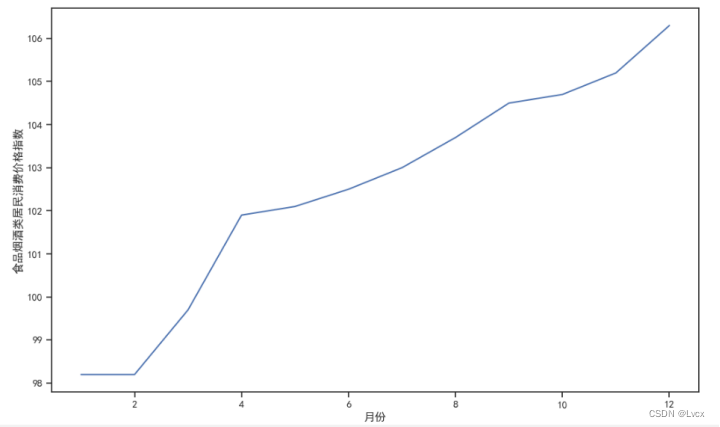
食品烟酒类居民消费价格指数集中在98.2~106.3范围内，
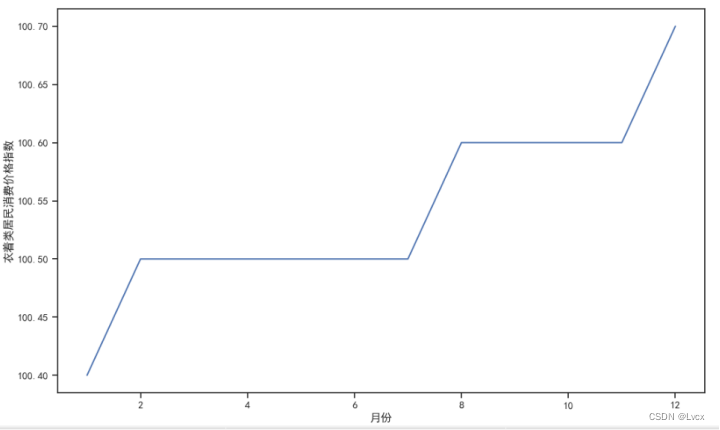
衣着类居民消费价格指数集中在100.4~100.7范围内，
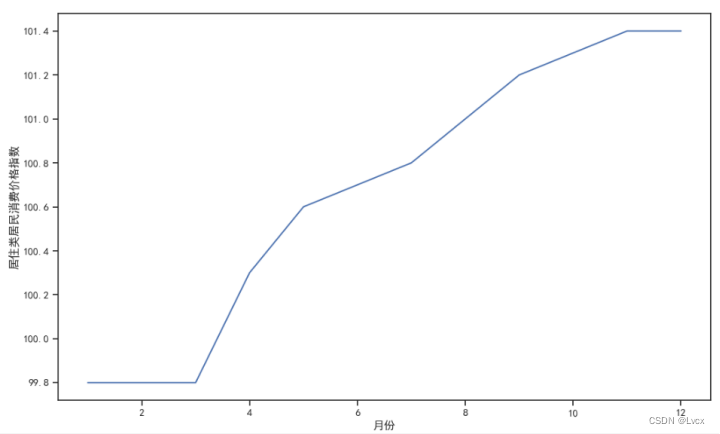
居住类居民消费价格指数在99.8~101.4范围内，
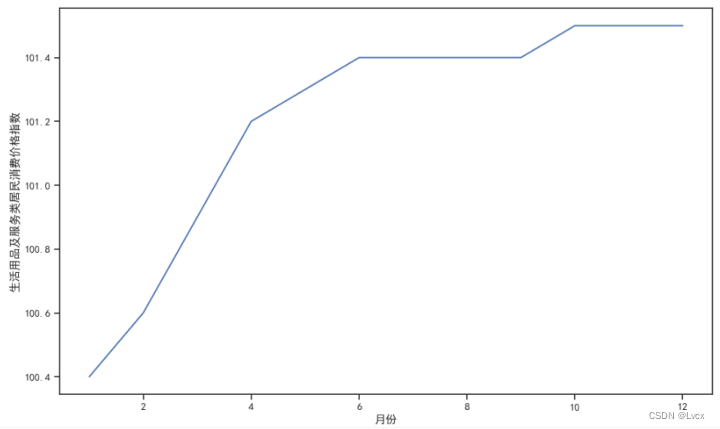
生活用品及服务类居民消费价格指数在100.4~101.5范围内，
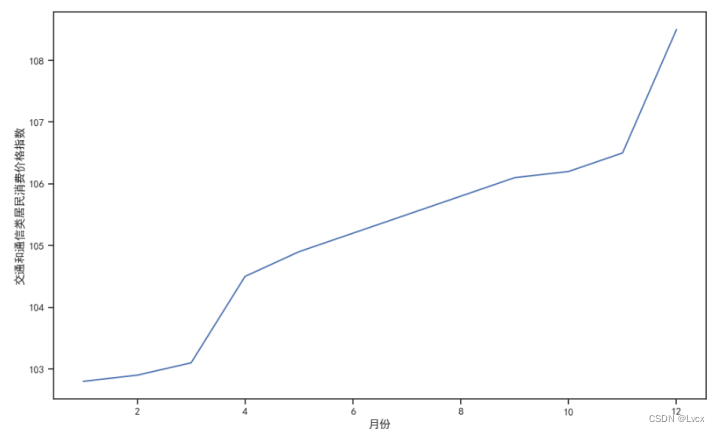
交通和通信类居民消费价格指数在102.8~108.5范围内，
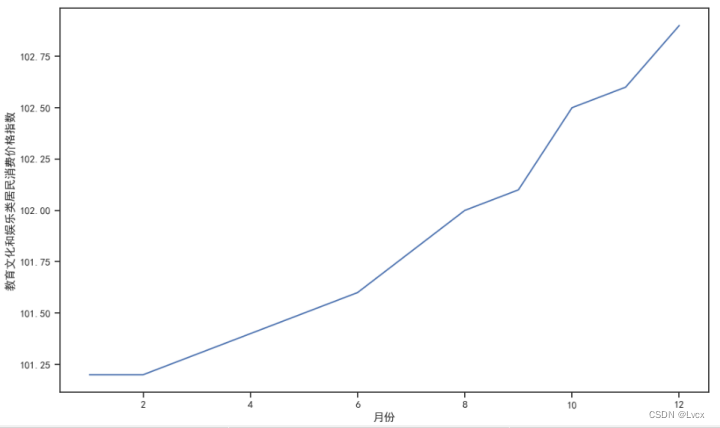
教育文化和娱乐居民消费价格指数在101.2~102.9范围内，
医疗保健类居民消费价格指数在100.5~100.7范围内，
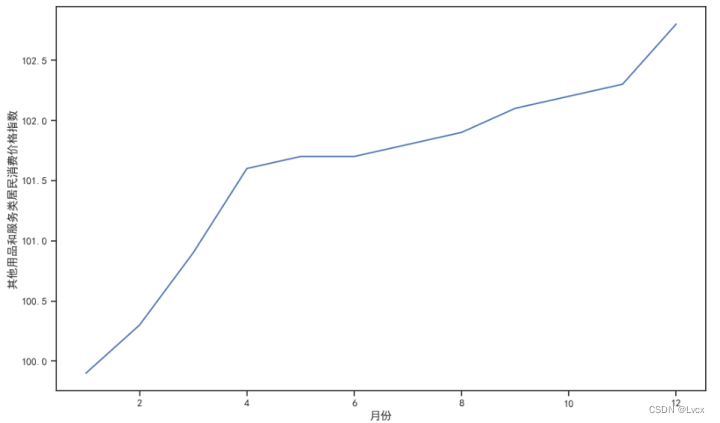
其他用品和服务类居民消费价格指数在99.9~102.8范围内。
2.离散程度分析
2022年全年的居民消费价格指数分布在100.9、101.5、101.6、101.8、102.1、102.5、102.7、102.8这几个指数上；
食品烟酒类居民消费价格指数分布在98.2、99.7、101.9、102.1、102.5、103、103.7、104.5、104.7、105.2、106.3这几个指数上；
衣着类居民消费价格指数分布在100.4、100.5、100.6、100.7这几个数上；
居住类居民消费价格指数分布在99.8、100.3、100.6、100.7、100.8、101、101.2、101.3、101.4这几个数上；
生活用品及服务类居民消费价格指数分布在100.4、100.6、100.9、101.2、101.3、101.4、101.5这几个数上；
交通和通信类居民消费价格和指数分布在102.8、102.9、103.1、104.5、104.9、105.2、105.5、105.8、106.1、106.2、106.5、108.5这几个数上；
教育文化和娱乐类居民消费价格指数分布在101.2、101.3、101.4、101.5、101.6、101.8、102、102.1、102.5、102.6、102.9这几个数上；
医疗保健类居民消费价格指数分布在100.5、100.6、100.7这几个数上；
其他用品和服务类居民消费价格指数分布在99.9、100.3、100.9、101.6、101.7、101.8、101.9、102.1、102.2、102.3、102.8这几个数上。
3.分布形状分析
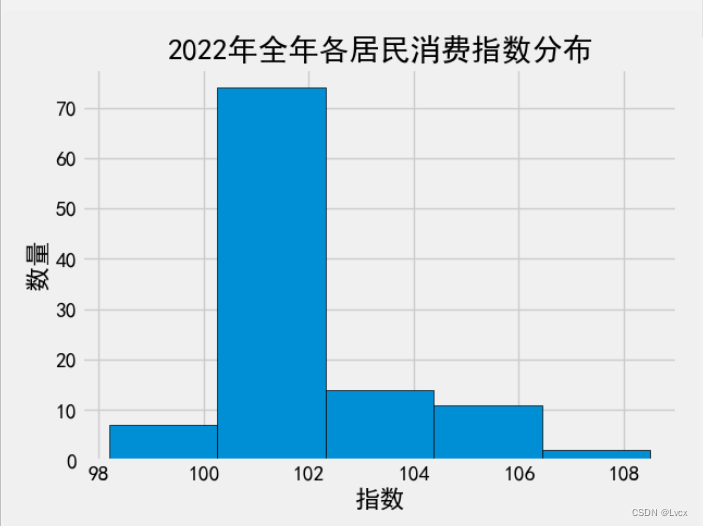
数值集中分布在98到108之间，以100为分界点，大于100的指数值偏多，只有几个是小于100的。

7. 用Matplotlib绘制直方图、折线图、柱状图（条形图）、饼图、箱线图、散点图、回归图

1.直方图

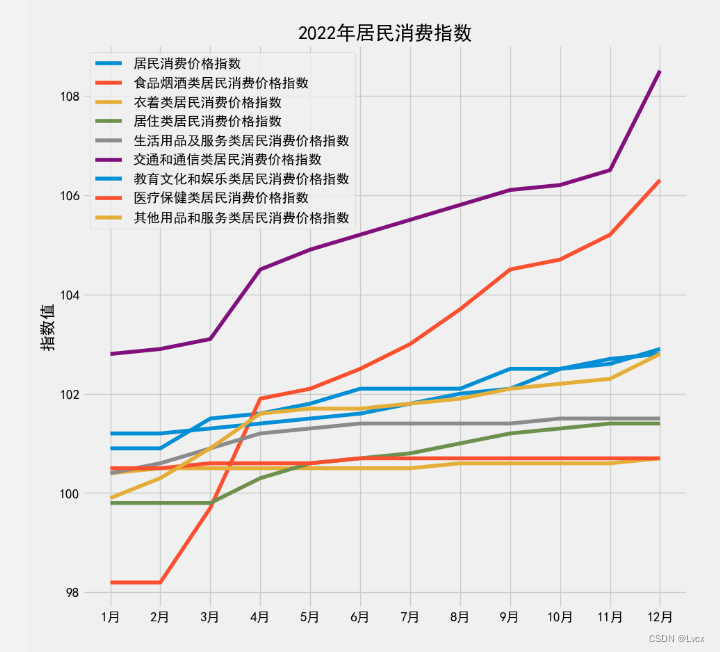
在这里插入图片描述

2.折线图

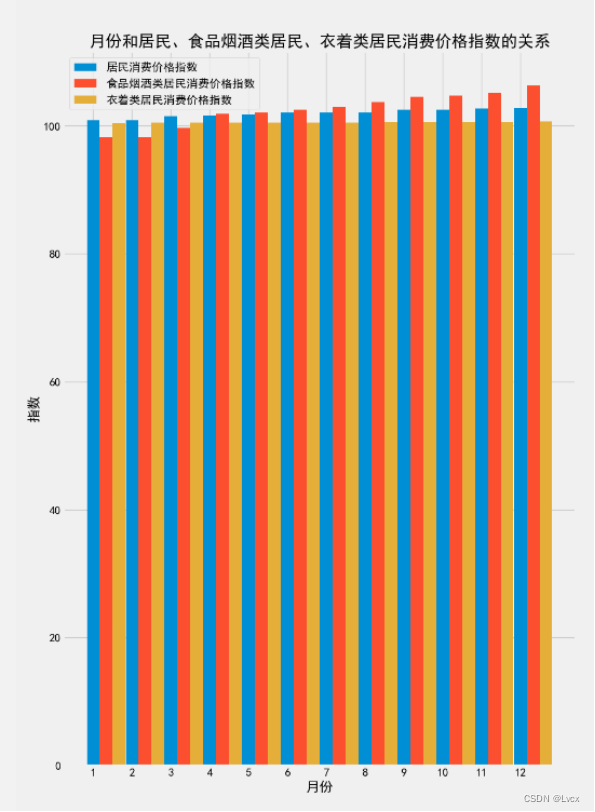
在这里插入图片描述

3.柱状图（条形图）

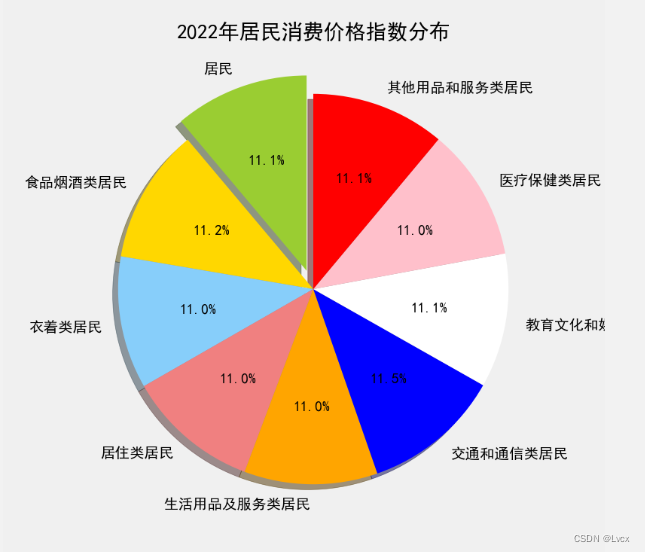
在这里插入图片描述

4.饼图

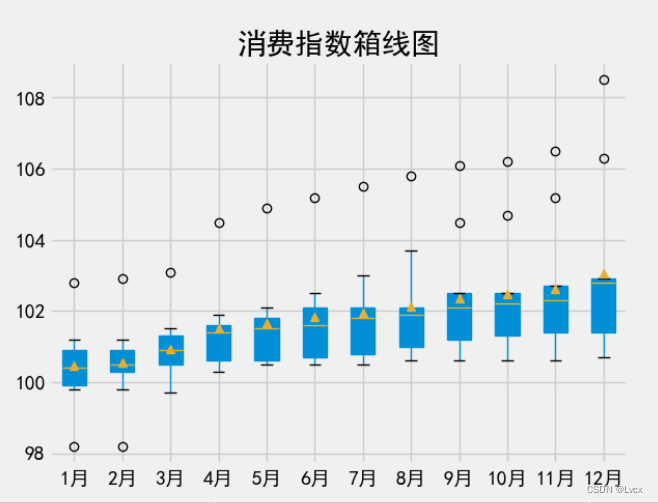
在这里插入图片描述

5.箱线图

箱型图包含一组数据：中位数、上四分位数、下四分位数、内限、外限、异常值。

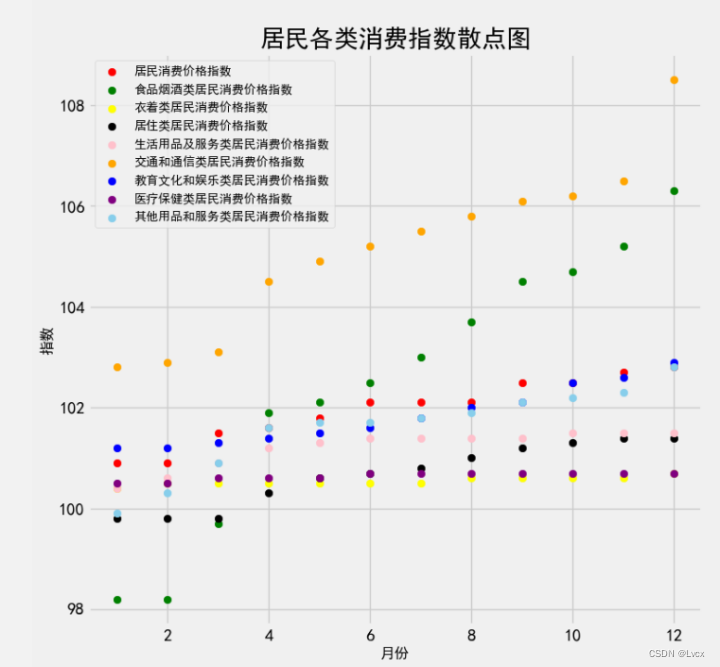
在这里插入图片描述

6.散点图

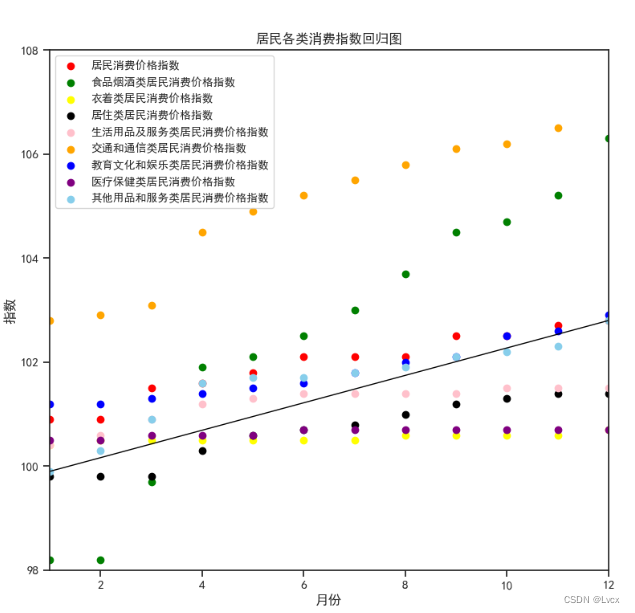
在这里插入图片描述

7.回归图

在这里插入图片描述

8.用Seaborn绘制直方图、折线图、柱状图（条形图）、饼图、箱线图、散点图、回归图

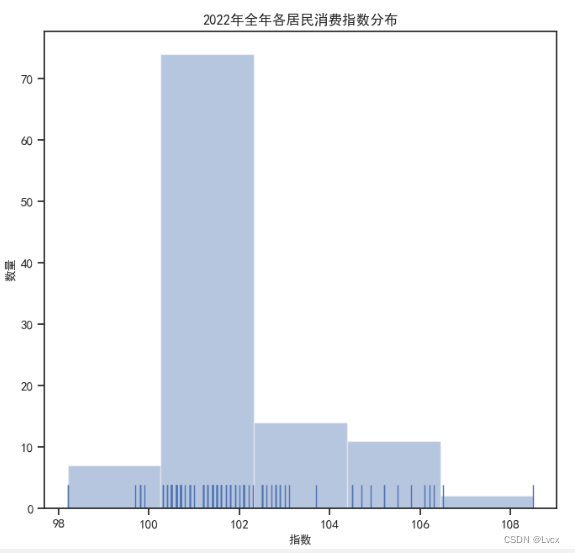
1.直方图

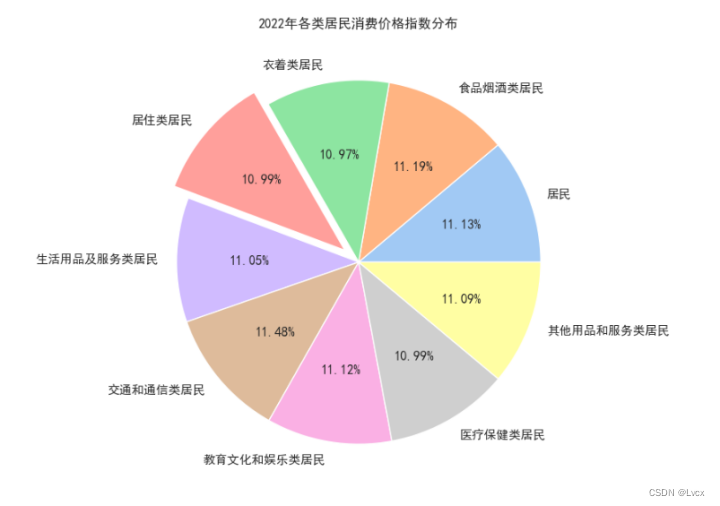
在这里插入图片描述

2.折线图

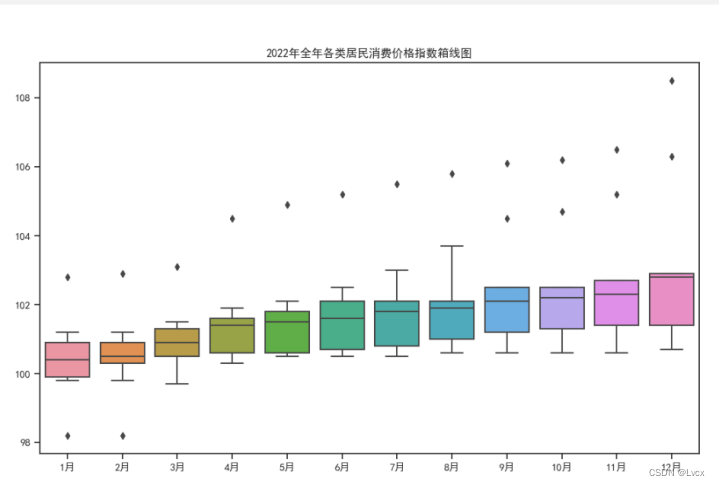
在这里插入图片描述
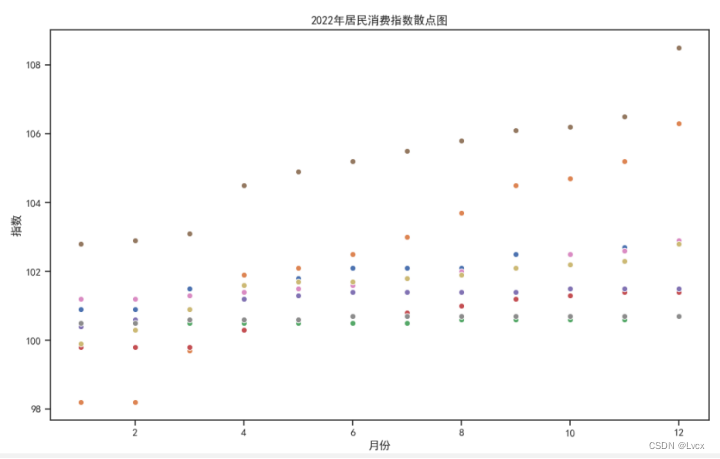
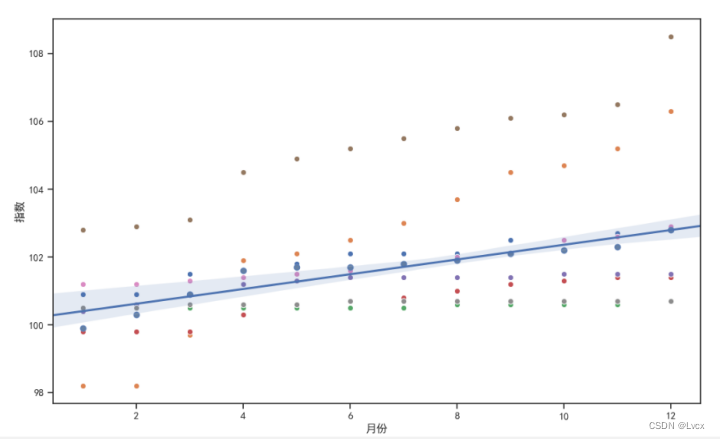
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述在这里插入图片描述

3.柱状图（条形图）

在这里插入图片描述

4.饼图

在这里插入图片描述

5.箱线图

在这里插入图片描述

6.散点图

在这里插入图片描述

7.回归图

在这里插入图片描述

9. 源代码

import numpy as np
import math
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns


# 四分位数有三个，第一个四分位数称为下四分位数，第二个四分位数就是中位数，第三个四分位数称为上四分位数
def quantile_exc(data, n):  # 其中data为数据组，n为第几个四分位数
    if n < 1 or n > 3:
        return False
    data.sort()     # 给数据排序
    position = (len(data) + 1)*n/4
    pos_integer = int(math.modf(position)[1])
    pos_decimal = position - pos_integer
    quartile = data[pos_integer - 1] + (data[pos_integer] - data[pos_integer - 1])*pos_decimal
    return quartile


def get_range(data_list):     # 得到极差
    data_list.sort()
    return data_list[-1] - data_list[0]


def get_value_and_count(data_list):    # 得到数值以及其计数
    data_list.sort()
    no_repeat_list = []
    for item in data_list:
        if item not in no_repeat_list:
            no_repeat_list.append(item)
    for item in no_repeat_list:
        count = data_list.count(item)
        print(item, ": ", count)


if __name__ == "__main__":
    # 1. 从csv文件中读取数据
    with open("./2022年月度数据.csv", "r", encoding="gbk") as f:
        head = f.readline().strip().split(",")   # 横行表头
        # print(head)
        data_list = [item.strip().split(",") for item in f.readlines()]   # 数据内容列表
        # print(data_list)
    # 将数据列表转换成字典：
    data_dict = {}
    for item in data_list:
        data_dict[item[0]] = [eval(item) for item in item[1:]]
    # print(data_dict)
    #  遍历使用到的数据：
    for name, data in data_dict.items():
        print(name, data)
    # 2. 计算均值、中位数、上及下四分位数 ==================================
    # 2.1 计算均值：
    print("----------------均值----------------------")
    means_dict = {}
    for name, data in data_dict.items():
        name += "_均值"
        mean = round(np.mean(data), 2)
        means_dict[name] = mean
        print(name, ": ", mean)   # 名称：均值
    # print(means_dict)
    # 2.2 计算中位数（排序统计中间值）
    print("----------------中位数----------------------")
    median_dict = {}
    for name, data in data_dict.items():
        name += "_中位数"
        a_median = round(quantile_exc(data, 2), 2)
        median_dict[name] = a_median
        print(name, ": ", a_median)     # 名称：中位数
    # 2.3 计算上四分位数
    print("---------------上四分位数-------------------")
    up_quantile_dict = {}
    for name, data in data_dict.items():
        name += "_上四分位数"
        a_quantile = round(quantile_exc(data, 3), 2)  # 保留两位小数
        up_quantile_dict[name] = a_quantile
        print(name, ": ", a_quantile)  # 名称：上四分位数
    # 2.4 计算下四分位数
    print("---------------下四分位数-------------------")
    down_quantile_dict = {}
    for name, data in data_dict.items():
        name += "_下四分位数"
        a_quantile = round(quantile_exc(data, 1), 2)  # 保留两位小数
        down_quantile_dict[name] = a_quantile
        print(name, ": ", a_quantile)  # 名称：上四分位数

    # 3. 计算极差、四分位差、方差、标准差、变异系数
    # 3.1 计算极差：最大值-最小值
    print("--------------极差---------------")
    range_dict = {}
    for name, data in data_dict.items():
        name += "_极差"
        a_range = round(get_range(data), 2)
        range_dict[name] = a_range
        print(name, ": ", a_range)
    # 3.2 计算四分位差：  上四分位数-下四分位数
    print("--------------四分位差------------")
    interquartile_difference = {}
    for name in data_dict.keys():
        name1 = name +"_四分位差"
        name2 = name + "_上四分位数"
        name3 = name + "_下四分位数"
        for i in range(len(data_dict)):
            a_interqurtile = round(up_quantile_dict[name2] - down_quantile_dict[name3], 2)
            interquartile_difference[name1] = a_interqurtile
        print(name, ": ", a_interqurtile)
    # 3.3 计算方差
    print("--------------方差----------------")
    var_dict = {}
    for name, data in data_dict.items():
        name += "_方差"
        a_var = round(np.var(data), 2)
        var_dict[name] = a_var
        print(name, ": ", a_var)
    # 3.4 计算标准差
    print("--------------标准差----------------")
    std_dict = {}
    for name, data in data_dict.items():
        name += "_标准差"
        a_std = round(np.std(data, ddof=1), 2)
        std_dict[name] = a_std
        print(name, ": ", a_std)
    # 3.5 计算变异系数：标准差/均值
    print("-------------变异系数---------------")
    coefficient_dict = {}
    for name in data_dict.keys():
        name1 = name + "_变异系数"
        name2 = name + "_标准差"
        name3 = name + "_均值"
        for i in range(len(data_dict)):
            a_coefficient = std_dict[name2]/means_dict[name3]
            coefficient_dict[name1] = a_coefficient
        print(name, ": ", a_coefficient)
    # 4. 集中趋势分析、离散程度分析、分布形状分析
    # 4.1 集中趋势分析：统计不同指数的出现次数
    print("------------集中和离散趋势分析-------------")
    central_trend_analysis = ""
    for name, data in data_dict.items():
        print(name, ":")
        get_value_and_count(data)
    # 5. 用Matplotlib和Seaborn绘制直方图、折线图、柱状图（条形图）、饼图、箱线图、散点图、回归图
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    # 5.1 绘制直方图
    # （1）matplotlib
    all_data = []
    for name, data in data_dict.items():
        all_data += data
    # print(all_data)
    plt.style.use("fivethirtyeight")
    plt.hist(all_data, bins=5, edgecolor="black")
    plt.title('2022年全年各居民消费指数分布')
    plt.xlabel('指数')
    plt.ylabel('数量')
    plt.tight_layout()
    plt.show()
    # （2）seaborn
    sns.set_context({'figure.figsize': [7, 7]})
    rc = {'font.sans-serif': 'SimHei',
          'axes.unicode_minus': False}
    sns.set(context="notebook", style="ticks", rc=rc)
    dis = sns.distplot(all_data, bins=5, kde=False, rug=True)
    dis.set_title("2022年全年各居民消费指数分布")
    dis.set_xlabel("指数", fontsize=10)
    dis.set_ylabel("数量", fontsize=10)
    # 5.2 绘制折线图
    # (1) matplotlib
    plt.figure(figsize=(10, 10))
    data1 = data_dict["居民消费价格指数"]
    data2 = data_dict["食品烟酒类居民消费价格指数"]
    data3 = data_dict["衣着类居民消费价格指数"]
    data4 = data_dict["居住类居民消费价格指数"]
    data5 = data_dict["生活用品及服务类居民消费价格指数"]
    data6 = data_dict["交通和通信类居民消费价格指数"]
    data7 = data_dict["教育文化和娱乐类居民消费价格指数"]
    data8 = data_dict["医疗保健类居民消费价格指数"]
    data9 = data_dict["其他用品和服务类居民消费价格指数"]
    x = range(12)
    x_ticks = [f"{i}月" for i in range(1, 13)]
    plt.xticks(x, x_ticks)
    plt.ylabel("指数值")   # 给y轴加名称
    # 添加标题
    plt.title("2022年居民消费指数")
    plt.plot(x, data1, label="居民消费价格指数")
    plt.plot(x, data2, label="食品烟酒类居民消费价格指数")
    plt.plot(x, data3, label="衣着类居民消费价格指数")
    plt.plot(x, data4, label="居住类居民消费价格指数")
    plt.plot(x, data5, label="生活用品及服务类居民消费价格指数")
    plt.plot(x, data6, label="交通和通信类居民消费价格指数")
    plt.plot(x, data7, label="教育文化和娱乐类居民消费价格指数")
    plt.plot(x, data8, label="医疗保健类居民消费价格指数")
    plt.plot(x, data9, label="其他用品和服务类居民消费价格指数")
    plt.legend(loc="best")
    plt.show()
    # (2) seaborn
    sns.set_context({'figure.figsize': [11, 7]})
    # 显示所有列
    pd.set_option('display.max_columns', None)
    # 显示所有行
    pd.set_option('display.max_rows', None)
    df = pd.DataFrame(data_dict)
    df.insert(9, "月份", [i for i in range(1, 13)], allow_duplicates=False)
    print(df)
    sns.lineplot(x="月份", y="居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="食品烟酒类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="衣着类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="居住类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="生活用品及服务类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="交通和通信类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="教育文化和娱乐类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="医疗保健类居民消费价格指数", data=df)
    plt.show()
    sns.lineplot(x="月份", y="其他用品和服务类居民消费价格指数", data=df)
    plt.show()
    # 5.3 柱状图
    # （1）matplotlib
    plt.figure(figsize=(10, 15))
    month_x = [i for i in range(1, 13)]
    x_indexes = np.arange(len(data1))
    width = 0.33
    plt.bar(x_indexes, data1, width=width, label="居民消费价格指数")
    plt.bar(x_indexes + width, data2, width=width, label="食品烟酒类居民消费价格指数")
    plt.bar(x_indexes + width*2, data3, width=width, label="衣着类居民消费价格指数")

    plt.xlabel("月份")
    plt.ylabel("指数")
    plt.title("月份和居民、食品烟酒类居民、衣着类居民消费价格指数的关系")
    plt.legend()
    plt.xticks(ticks=x_indexes, labels=month_x)
    plt.legend(loc="best")
    plt.show()
    # （2）seaborn
    sns.set_context({'figure.figsize': [11, 7]})
    sns.barplot(x="月份", y="食品烟酒类居民消费价格指数", data=df)
    # 5.4 饼图
    # （1）matplotlib
    plt.figure(figsize=(8, 8))
    data1_sum = sum(data1)
    data2_sum = sum(data2)
    data3_sum = sum(data3)
    data4_sum = sum(data4)
    data5_sum = sum(data5)
    data6_sum = sum(data6)
    data7_sum = sum(data7)
    data8_sum = sum(data8)
    data9_sum = sum(data9)
    all_sum = sum([data1_sum, data2_sum, data3_sum, data4_sum, data5_sum, data6_sum, data7_sum,data8_sum, data9_sum])
    data1_per = round(data1_sum / (all_sum/100), 2)
    data2_per = round(data2_sum / (all_sum/100), 2)
    data3_per = round(data3_sum / (all_sum/100), 2)
    data4_per = round(data4_sum / (all_sum/100), 2)
    data5_per = round(data5_sum / (all_sum/100), 2)
    data6_per = round(data6_sum / (all_sum/100), 2)
    data7_per = round(data7_sum / (all_sum/100), 2)
    data8_per = round(data8_sum / (all_sum/100), 2)
    data9_per = round(data9_sum / (all_sum/100), 2)
    # print(data1_per+data2_per+data3_per+data4_per+data5_per+data6_per+data7_per+data8_per+data9_per)
    size = [data1_per, data2_per, data3_per, data4_per, data5_per, data6_per, data7_per, data8_per, data9_per]
    labels = ["居民", "食品烟酒类居民", "衣着类居民",
              "居住类居民", "生活用品及服务类居民", "交通和通信类居民",
              "教育文化和娱乐类居民", "医疗保健类居民", "其他用品和服务类居民"]
    colors = ['yellowgreen', 'gold', 'lightskyblue', 'lightcoral', "orange", "blue", "white", "pink", "red"]
    explode = (0.1, 0, 0, 0, 0, 0, 0, 0, 0)     # 突出显示第一个扇形
    plt.pie(size, explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=90)
    plt.title("2022年居民消费价格指数分布")
    plt.show()
    # （2） seaborn
    colors = sns.color_palette('pastel')
    explode = (0, 0, 0, 0.1, 0, 0, 0, 0, 0)
    plt.pie(size, labels=labels, explode=explode, colors=colors, autopct="%1.2f%%")
    plt.title("2022年各类居民消费价格指数分布")
    plt.show()
    # 5.5 箱线图
    # （1） matplotlib
    df1 = pd.DataFrame([data1, data2, data3, data4, data5, data6, data7, data8, data9], columns=['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月', '12月'])
    f = df1.boxplot(sym='o',  # 异常点形状
                   vert=True,  # 是否垂直
                   whis=1.5,  # IQR
                   patch_artist=True,  # 上下四分位框是否填充
                   meanline=False, showmeans=True,  # 是否有均值线及其形状
                   showbox=True,  # 是否显示箱线
                   showfliers=True,  # 是否显示异常值
                   notch=False,  # 中间箱体是否缺口
                   return_type='dict')  # 返回类型为字典
    plt.title('消费指数箱线图')
    plt.show()
    # （2）seaborn
    box = sns.boxplot(data=df1)
    box.set_title("2022年全年各类居民消费价格指数箱线图")
    plt.show()
    # 5.6 散点图
    # （1）matplotlib
    plt.figure(figsize=(8, 8))    # 设置画布大小
    x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])

    y = np.array(data1)
    plt.scatter(x, y, color='red', label='居民消费价格指数')

    y = np.array(data2)
    plt.scatter(x, y, color='green', label='食品烟酒类居民消费价格指数')

    y = np.array(data3)
    plt.scatter(x, y, color='yellow', label='衣着类居民消费价格指数')

    y = np.array(data4)
    plt.scatter(x, y, color='black', label='居住类居民消费价格指数')

    y = np.array(data5)
    plt.scatter(x, y, color='pink', label='生活用品及服务类居民消费价格指数')

    y = np.array(data6)
    plt.scatter(x, y, color='orange', label='交通和通信类居民消费价格指数')

    y = np.array(data7)
    plt.scatter(x, y, color='blue', label='教育文化和娱乐类居民消费价格指数')

    y = np.array(data8)
    plt.scatter(x, y, color='purple', label='医疗保健类居民消费价格指数')

    y = np.array(data9)
    plt.scatter(x, y, color='skyblue', label='其他用品和服务类居民消费价格指数')
    plt.legend(loc='best', fontsize=10)

    plt.xlabel("月份", fontdict={'size': 12})
    plt.ylabel("指数", fontdict={'size': 12})
    plt.title("居民各类消费指数散点图")
    plt.show()
    # （2）seaborn
    data_plot = pd.DataFrame({"月份": x, "指数": data1})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data2})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data3})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data4})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data5})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data6})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data7})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data8})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data9})
    sc = sns.scatterplot(x="月份", y="指数", data=data_plot)
    sc.set_title("2022年居民消费指数散点图")
    plt.show()
    # 5.7 回归图
    # （1）matplotlib
    # 绘制散点
    plt.figure(figsize=(8, 8))  # 设置画布大小
    x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])

    y = np.array(data1)
    plt.scatter(x, y, color='red', label='居民消费价格指数')

    y = np.array(data2)
    plt.scatter(x, y, color='green', label='食品烟酒类居民消费价格指数')

    y = np.array(data3)
    plt.scatter(x, y, color='yellow', label='衣着类居民消费价格指数')

    y = np.array(data4)
    plt.scatter(x, y, color='black', label='居住类居民消费价格指数')

    y = np.array(data5)
    plt.scatter(x, y, color='pink', label='生活用品及服务类居民消费价格指数')

    y = np.array(data6)
    plt.scatter(x, y, color='orange', label='交通和通信类居民消费价格指数')

    y = np.array(data7)
    plt.scatter(x, y, color='blue', label='教育文化和娱乐类居民消费价格指数')

    y = np.array(data8)
    plt.scatter(x, y, color='purple', label='医疗保健类居民消费价格指数')

    y = np.array(data9)
    plt.scatter(x, y, color='skyblue', label='其他用品和服务类居民消费价格指数')
    plt.legend(loc='best', fontsize=10)

    plt.xlabel("月份", fontdict={'size': 12})
    plt.ylabel("指数", fontdict={'size': 12})
    plt.title("居民各类消费指数回归图")
    # 绘制回归线
    x_mean = np.mean(month_x)
    y_mean = np.mean(data3)
    m1 = 0  # 分母
    m2 = 0  # 分子
    for x_i, y_i in zip(month_x, data3):
        m1 += (x_i - x_mean) * (y_i - y_mean)
        m2 += (x_i - x_mean) ** 2
    a = m1 / m2
    b = y_mean - a * x_mean
    print(a, b)
    y_line = [a * x + b for x in data3]
    print(x)
    print(y_line)
    plt.plot([1, 12], [99.9, 102.8], color="black", linewidth=1, label="回归线")
    plt.axis([1, 12, 98, 108])
    plt.show()

    # （2）seaborn
    data_plot = pd.DataFrame({"月份": x, "指数": data1})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data2})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data3})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data4})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data5})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data6})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data7})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data8})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    data_plot = pd.DataFrame({"月份": x, "指数": data9})
    sns.scatterplot(x="月份", y="指数", data=data_plot)
    sns.regplot(x="月份", y="指数", data=data_plot)
    sc.set_title("2022年居民消费指数回归图")
    plt.show()


# 均值、方差、标准差：
# https://blog.csdn.net/robert_chen1988/article/details/102712946
# 中位数的计算：https://blog.csdn.net/Yiess/article/details/121102021
# 四分位数：https://blog.csdn.net/Changxing_J/article/details/106232995
# 极差、四分位差、方差、标准差、变异系数：https://blog.csdn.net/walking_visitor/article/details/83503008
# 方差、标准差：https://blog.csdn.net/Louise_Trender/article/details/105828562
# 变异系数：https://blog.csdn.net/Changxing_J/article/details/106233469
# matplotlib: https://matplotlib.org/devdocs/gallery/lines_bars_and_markers/barchart.html#sphx-glr-gallery-lines-bars-and-markers-barchart-py
# 绘图：https://blog.csdn.net/m0_56521890/article/details/129224416
# 直方图：https://blog.csdn.net/weixin_44327634/article/details/123745262

二、鸢尾花数据集

1. 数据来源

使用的数据来源网站：tensorflow.org
数据网站连接：http://download.tensorflow.org/data/iris_training.csv

2.下载数据

直接点击网页链接即可下载。
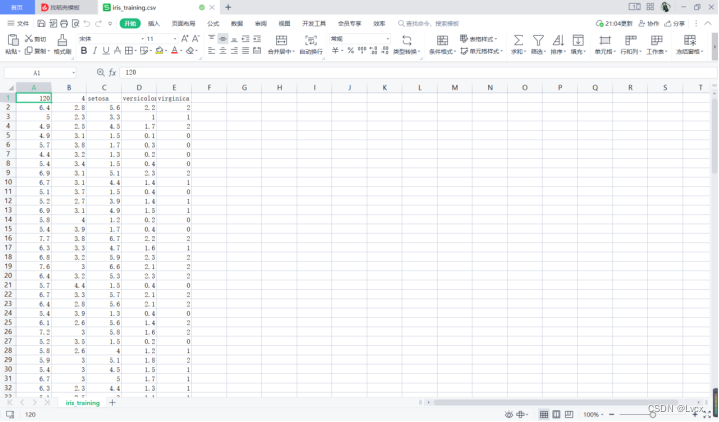
在这里插入图片描述

数据列代表的含义：
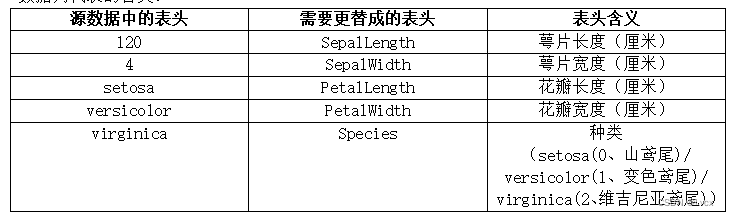
在这里插入图片描述

3. 集中趋势分析：求均值、中位数、上四分位数、下四分位数

5. 计算极差、四分位差、方差、标准差、变异系数(标准差/均值)

6. 用Matplotlib绘制直方图、折线图、柱状图（条形图）、饼图、箱线图、散点图、回归图

1.直方图

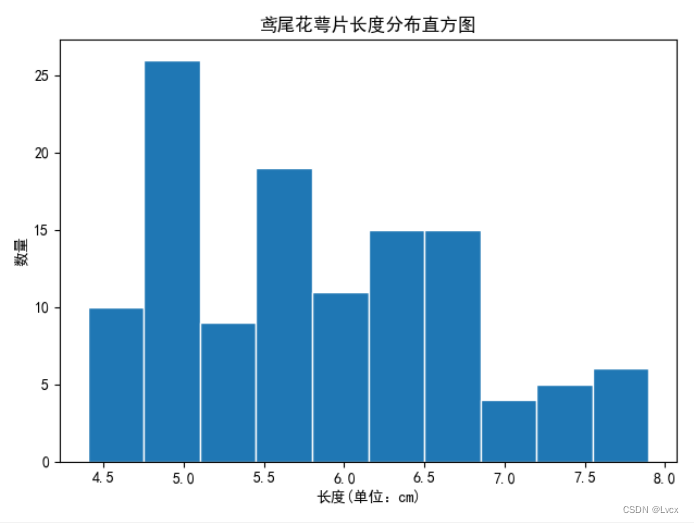
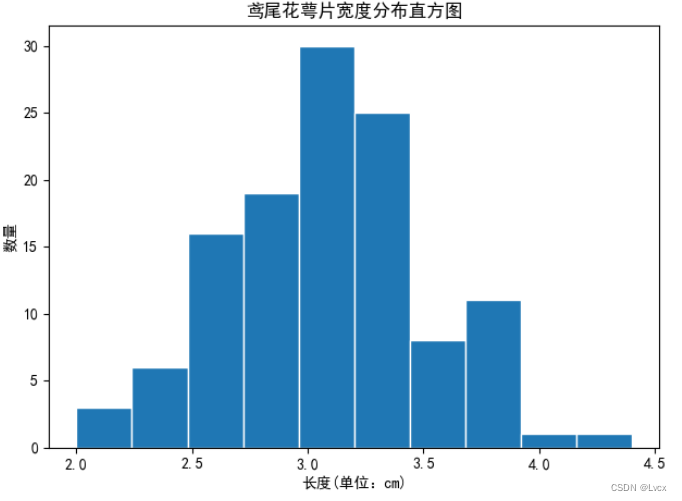
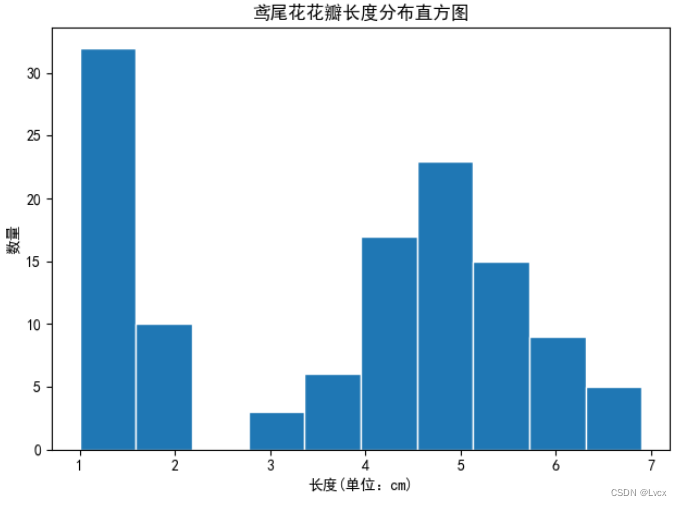
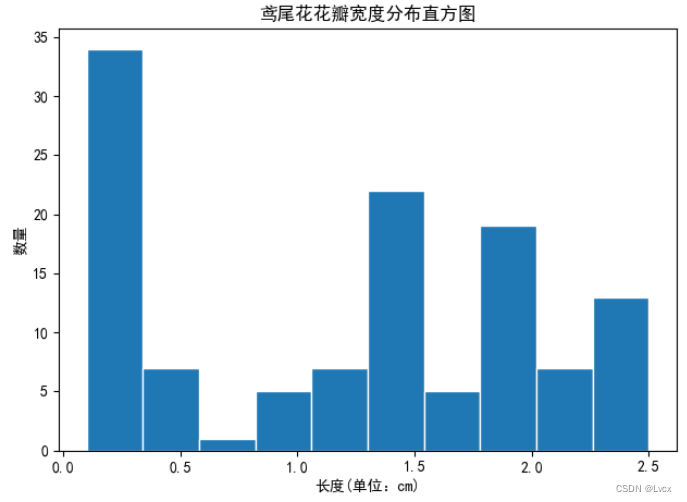
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.折线图

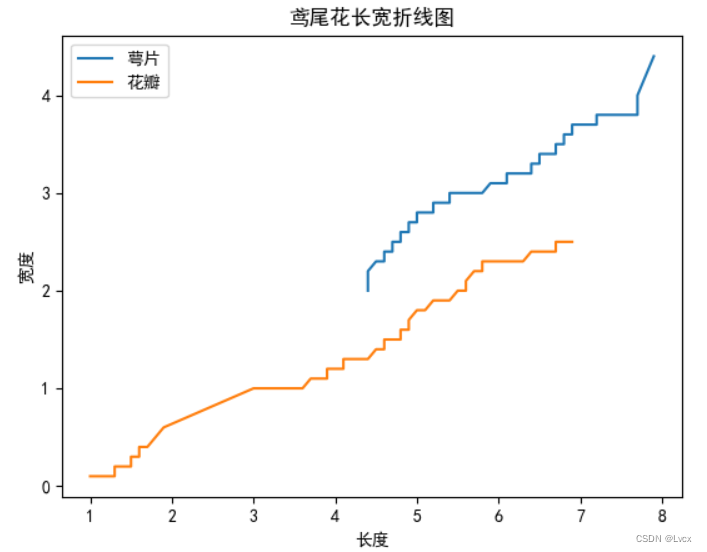
在这里插入图片描述

3.柱状图（条形图）

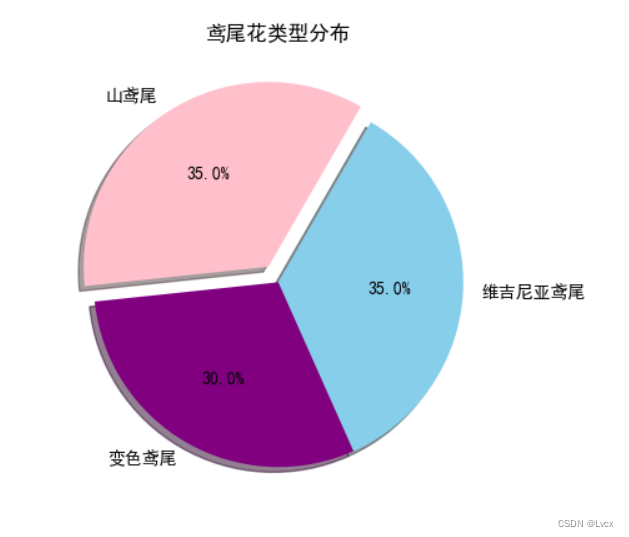
在这里插入图片描述

4.饼图

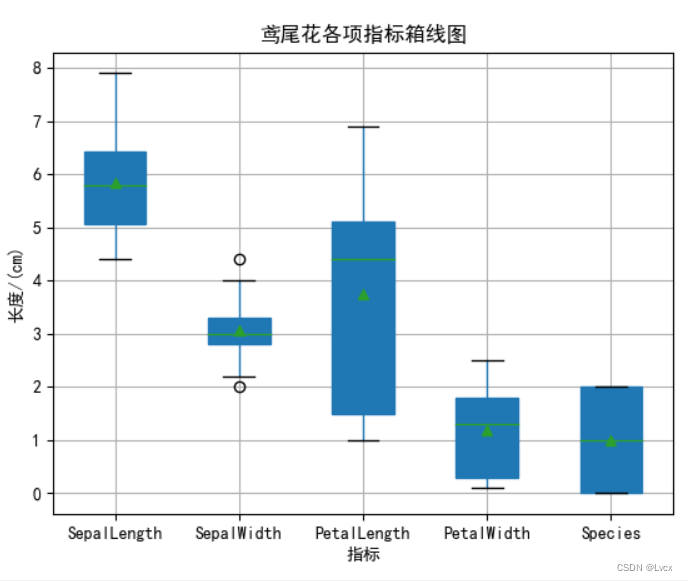
在这里插入图片描述

5.箱线图

箱型图包含一组数据：中位数、上四分位数、下四分位数、内限、外限、异常值。
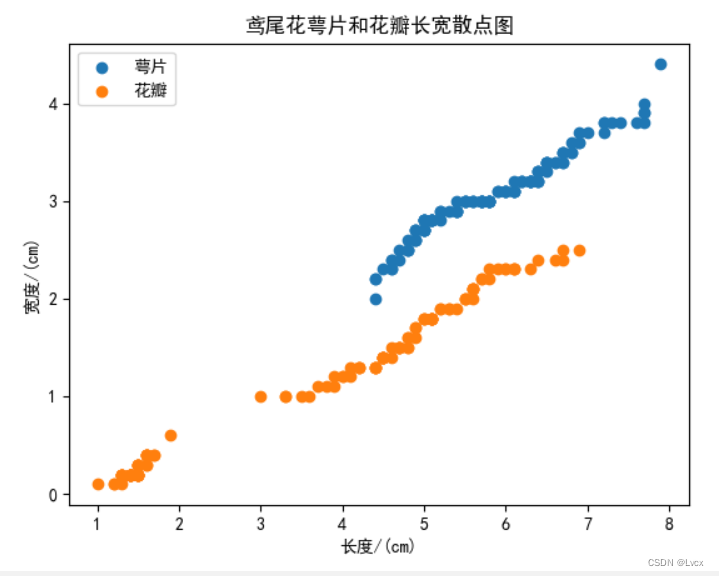
在这里插入图片描述

6.散点图

在这里插入图片描述

7.回归图
在这里插入图片描述

7.用Seaborn绘制直方图、折线图、柱状图（条形图）、饼图、箱线图、散点图、回归图

1.直方图

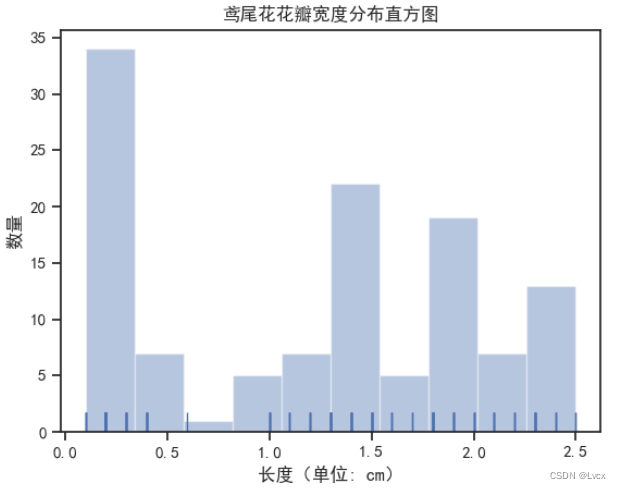
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

2.折线图

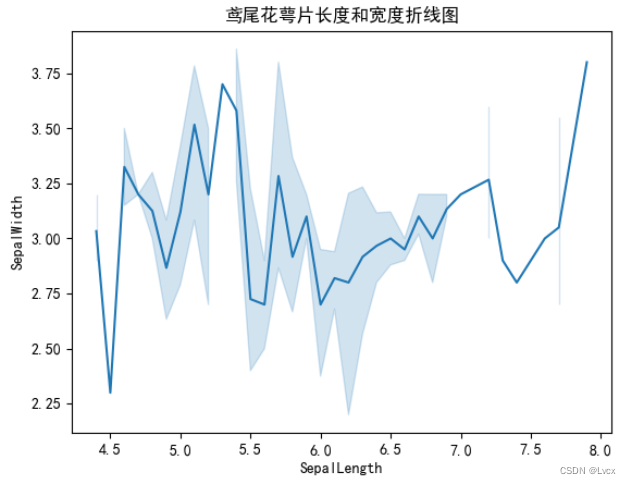
在这里插入图片描述
在这里插入图片描述

3.柱状图（条形图）

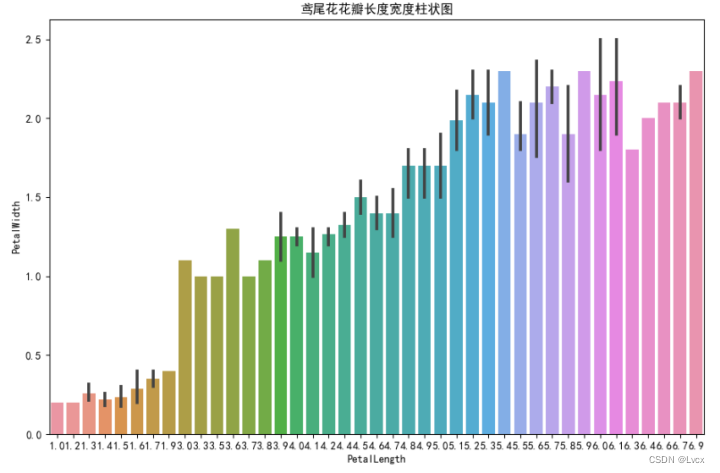
在这里插入图片描述

4.饼图

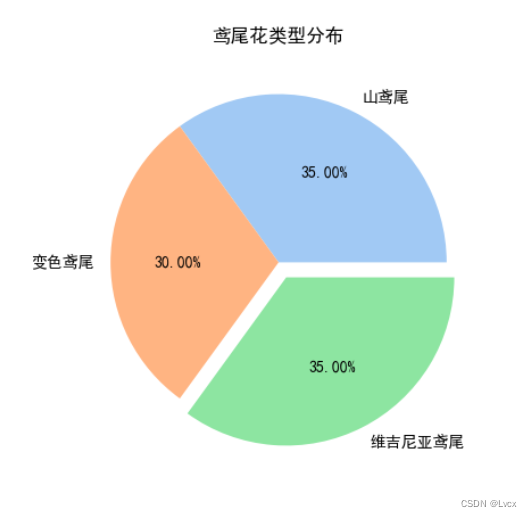
在这里插入图片描述

5.箱线图

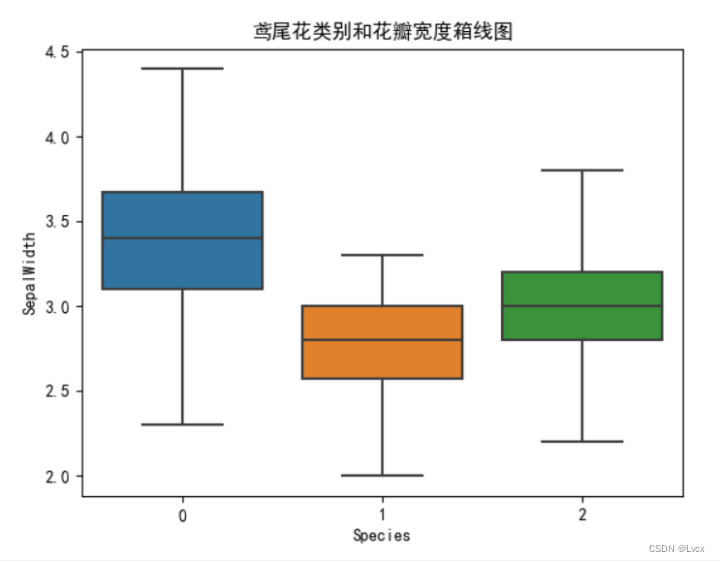
在这里插入图片描述

6.散点图

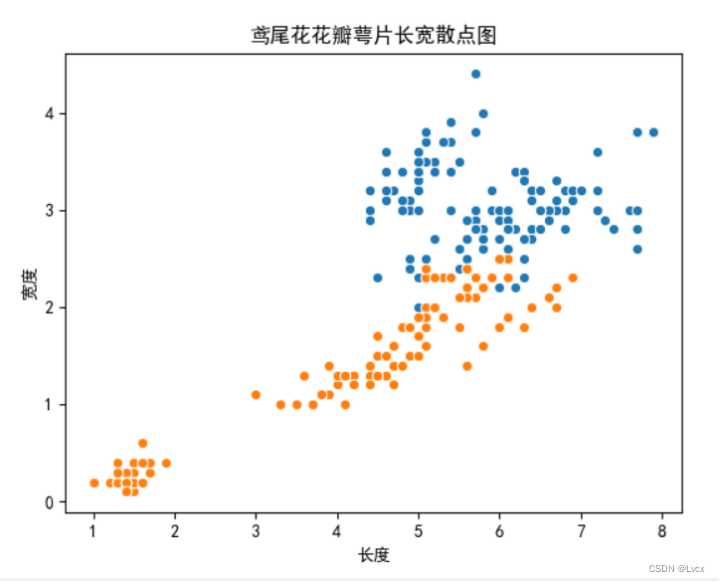
在这里插入图片描述

7.回归图

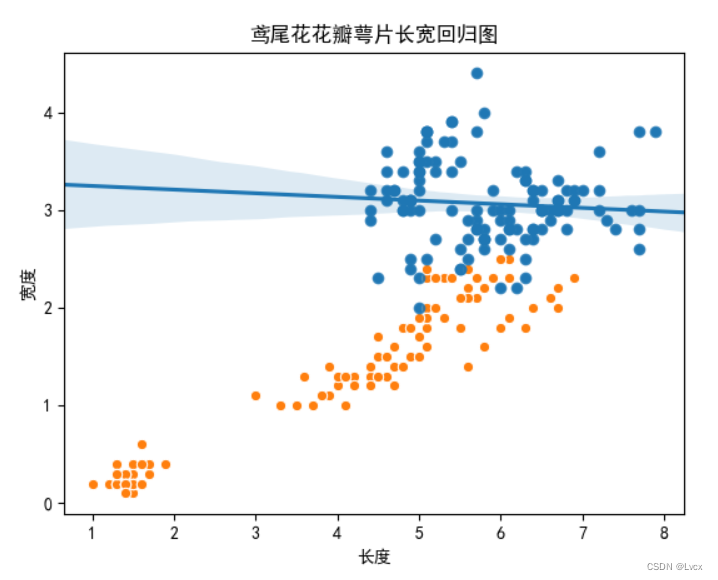
在这里插入图片描述

8. 源代码

import pandas as pd
import math
import numpy as np
from collections import Counter, defaultdict
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns


def get_average(data_list):   # 得到平均值
    data_length = len(data_list)
    data_sum = sum(data_list)
    return round(data_sum/data_length, 2)   # 保留两位小数


def get_median(data_list):   # 计算中位数
    data_list.sort()
    list_length = len(data_list)
    if list_length % 2 == 0:
        return (data_list[int(list_length / 2) - 1] + data_list[int(list_length / 2)]) / 2
    return data_list[int(list_length / 2)]


def get_quartile(data_list, x):    # 计算四分位数    # 1：下四分位数    # 3：上四分位数
    if x < 1 or x > 3:
        return False
    data_list.sort()     # 给数据排序
    position = (len(data_list) + 1)*x/4
    pos_integer = int(math.modf(position)[1])
    pos_decimal = position - pos_integer
    quartile = data_list[pos_integer - 1] + (data_list[pos_integer] - data_list[pos_integer - 1])*pos_decimal
    return quartile


def get_range(data_max, data_min):   # 获得极差、四分位差
    return round(data_max - data_min, 2)


def get_variance(data_list): # 获得方差
    return round(np.var(data_list), 2)


def get_std(data_list):   # 得到标准差
    return round(np.std(data_list, ddof=1), 2)


def get_coefficient(data_std, data_mean):    # 获得变异系数    标准差/均值
    return round(data_std / data_mean, 2)


def plt_picture_hist(data, name):     # matplotlib绘制直方图
    plt.hist(data, bins=10, edgecolor="white", label=name)
    plt.title(f'鸢尾花{name}分布直方图')
    plt.xlabel('长度(单位：cm)')
    plt.ylabel('数量')
    plt.tight_layout()
    plt.show()


def sns_picture_hist(data, name, rc):    # seaborn绘制直方图
    sns.set(context="notebook", style="ticks", rc=rc)
    dis = sns.distplot(data, bins=10, kde=False, rug=True)
    dis.set_title(f'鸢尾花{name}分布直方图')
    dis.set_xlabel("长度（单位: cm）")
    dis.set_ylabel("数量")
    plt.show()


def plt_picture_plot(x1, y1, x2, y2):  # 绘制折线图
    # x 是长度，y是宽度
    plt.xlabel("长度")
    plt.ylabel("宽度")
    plt.title("鸢尾花长宽折线图")
    plt.plot(x1, y1, label="萼片")
    plt.plot(x2, y2, label="花瓣")
    plt.legend(loc="best")
    plt.show()


def main():
    # 获取数据
    columns = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Species']
    df_iris = pd.read_csv("./iris_training.csv", header=0, names=columns)
    # print(df_iris)
    SepalLength = list(df_iris['SepalLength']) # 取出指定列，萼片长度
    SepalWidth = list(df_iris['SepalWidth'])    # 取出指定列， 萼片宽度
    PetalLength = list(df_iris['PetalLength'])  # 取出指定列，花瓣长度
    PetalWidth = list(df_iris['PetalWidth'])    # 取出指定列， 花瓣宽度
    Species = list(df_iris['Species'])   # 取出种类
    # ===================================================================
    # 1. 平均值
    mean1 = get_average(SepalLength)
    print("萼片长度平均值：", mean1, "cm")
    mean2 = get_average(SepalWidth)
    print("萼片宽度平均值：", mean2, "cm")
    mean3 = get_average(PetalLength)
    print("花瓣长度平均值：", mean3, "cm")
    mean4 = get_average(PetalWidth)
    print("花瓣宽度平均值：", mean4, "cm")
    print()
    # 2. 中位数
    print("萼片长度中位数：", get_median(SepalLength), "cm")
    print("萼片宽度中位数：", get_median(SepalWidth), "cm")
    print("花瓣长度中位数：", get_median(PetalLength), "cm")
    print("花瓣宽度中位数：", get_median(PetalWidth), "cm")
    print()
    # 3. 上四分位数
    up1 = get_quartile(SepalLength, 3)
    print("萼片长度上四分位数：", up1, "cm")
    up2 = get_quartile(SepalWidth, 3)
    print("萼片宽度上四分位数：", up2, "cm")
    up3 = get_quartile(PetalLength, 3)
    print("花瓣长度上四分位数：", up3, "cm")
    up4 = get_quartile(PetalWidth, 3)
    print("花瓣宽度上四分位数：", up4, "cm")
    print()
    # 4. 下四分位数
    down1 = get_quartile(SepalLength, 1)
    print("萼片长度下四分位数：", down1, "cm")
    down2 = get_quartile(SepalWidth, 1)
    print("萼片宽度下四分位数：", down2, "cm")
    down3 = get_quartile(PetalLength, 1)
    print("花瓣长度下四分位数：", down3, "cm")
    down4 = get_quartile(PetalWidth, 1)
    print("花瓣宽度下四分位数：", down4, "cm")
    print()
    # ===================================================================
    # 1. 极差
    print("萼片长度极差：", get_range(max(SepalLength), min(SepalLength)), "cm")
    print("萼片宽度极差：", get_range(max(SepalWidth), min(SepalWidth)), "cm")
    print("花瓣长度极差：", get_range(max(PetalLength), min(PetalLength)), "cm")
    print("花瓣宽度极差：", get_range(max(PetalWidth), min(PetalWidth)), "cm")
    print()
    # 2. 四分位差
    print("萼片长度四分位差：", get_range(up1, down1), "cm")
    print("萼片宽度四分位差：", get_range(up2, down2), "cm")
    print("花瓣长度四分位差：", get_range(up3, down3), "cm")
    print("花瓣宽度四分位差：", get_range(up4, down4), "cm")
    print()
    # 3. 方差
    print("萼片长度方差：", get_variance(SepalLength))
    print("萼片宽度方差：", get_variance(SepalWidth))
    print("花瓣长度方差：", get_variance(PetalLength))
    print("花瓣宽度方差：", get_variance(PetalWidth))
    print()
    # 4. 标准差
    std1 = get_std(SepalLength)
    print("萼片长度标准差：", std1)
    std2 = get_std(SepalWidth)
    print("萼片宽度标准差：", std2)
    std3 = get_std(PetalLength)
    print("花瓣长度标准差：", std3)
    std4 = get_std(PetalWidth)
    print("花瓣宽度标准差：", std4)
    print()
    # 5. 变异系数
    print("萼片长度变异系数：", get_coefficient(std1, mean1))
    print("萼片宽度变异系数：", get_coefficient(std2, mean2))
    print("花瓣长度变异系数：", get_coefficient(std3, mean3))
    print("花瓣宽度变异系数：", get_coefficient(std4, mean4))
    print()
    # ===================================================================
    matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 正常显示中文
    rc = {'font.sans-serif': 'SimHei',
          'axes.unicode_minus': False}
    # 1. 直方图
    # matplotlib
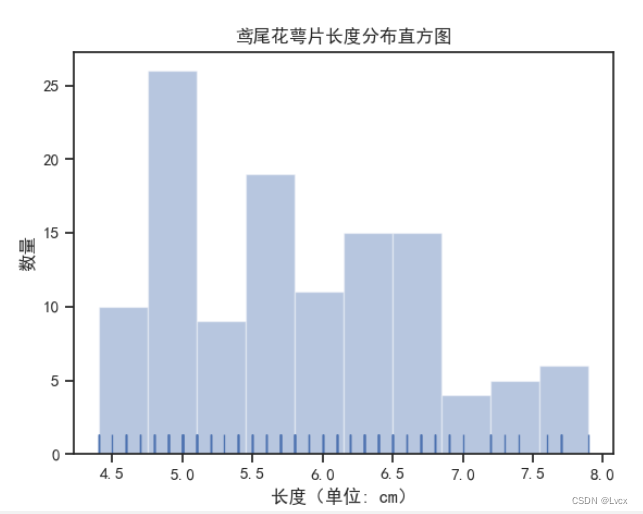
    plt_picture_hist(SepalLength, "萼片长度")
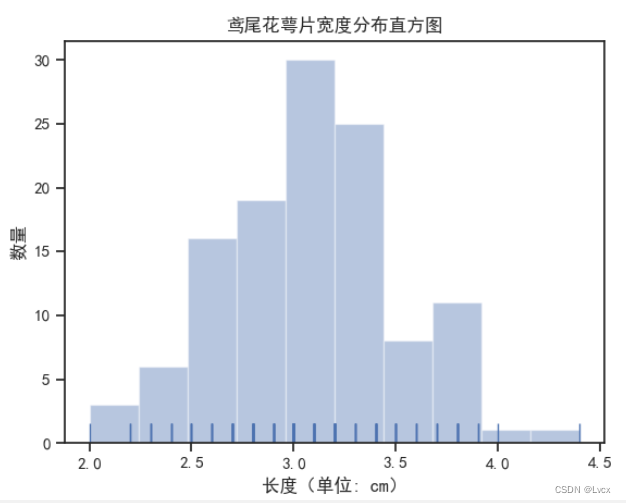
    plt_picture_hist(SepalWidth, "萼片宽度")
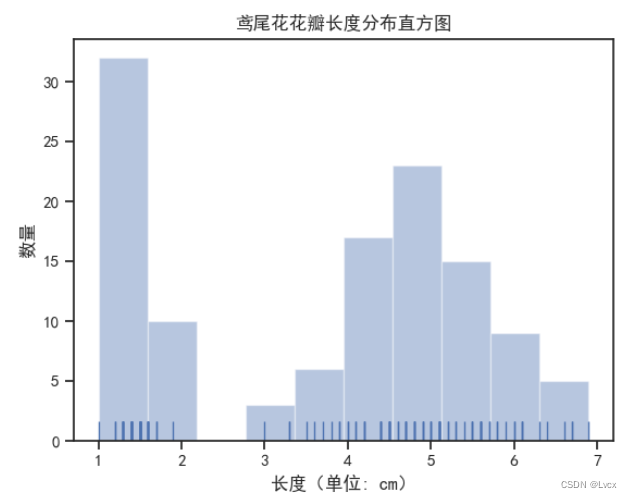
    plt_picture_hist(PetalLength, "花瓣长度")
    plt_picture_hist(PetalWidth, "花瓣宽度")
    # seaborn
    sns_picture_hist(SepalLength, "萼片长度", rc)
    sns_picture_hist(SepalWidth, "萼片宽度", rc)
    sns_picture_hist(PetalLength, "花瓣长度", rc)
    sns_picture_hist(PetalWidth, "花瓣宽度", rc)

    # 2. 折线图
    # matplotlib
    plt_picture_plot(SepalLength, SepalWidth, PetalLength, PetalWidth)
    # seaborn
    lin1=sns.lineplot(x="SepalLength", y="SepalWidth", data=df_iris)
    lin1.set_title("鸢尾花萼片长度和宽度折线图")
    plt.show()
    lin2 = sns.lineplot(x="PetalLength", y="PetalWidth", data=df_iris)
    lin2.set_title("鸢尾花花瓣长度和宽度折线图")
    plt.show()

    # 3.柱状图
    # matplotlib
    plt.bar(PetalLength, PetalWidth, edgecolor="white")
    plt.title("鸢尾花花瓣长度宽度柱状图")
    plt.xlabel("长度")
    plt.ylabel("宽度")
    plt.show()
    # seaborn
    sns.set_context({'figure.figsize': [11, 7]})
    bar = sns.barplot(x='PetalLength', y='PetalWidth', data=df_iris)  # 条形图
    bar.set_title("鸢尾花花瓣长度宽度柱状图")
    plt.show()

    # 4. 饼图
    # matplotlib
    setosa_0 = Species.count(0)
    versicolor_1 = Species.count(1)
    virginica_2 = Species.count(2)
    count_sum = setosa_0 + versicolor_1 + virginica_2
    sizes = [setosa_0/count_sum, versicolor_1/count_sum, virginica_2/count_sum]
    labels = ["山鸢尾", "变色鸢尾", "维吉尼亚鸢尾"]
    colors = ["pink", "purple", "skyblue"]
    explode = (0.1, 0, 0)
    plt.pie(sizes, explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=60)
    plt.title("鸢尾花类型分布")
    plt.show()
    # seaborn
    colors = sns.color_palette('pastel')
    explode = (0, 0, 0.1)
    plt.pie(sizes, labels=labels, explode=explode, colors=colors, autopct="%1.2f%%")
    plt.title("鸢尾花类型分布")
    plt.show()

    # 5. 箱线图
    # matplotlib
    df_iris.boxplot(sym='o',  # 异常点形状
                   vert=True,  # 是否垂直
                   whis=1.5,  # IQR
                   patch_artist=True,  # 上下四分位框是否填充
                   meanline=False, showmeans=True,  # 是否有均值线及其形状
                   showbox=True,  # 是否显示箱线
                   showfliers=True,  # 是否显示异常值
                   notch=False,  # 中间箱体是否缺口
                   return_type='dict')  # 返回类型为字典
    plt.ylabel("长度/(cm)")
    plt.xlabel("指标")
    plt.title('鸢尾花各项指标箱线图')
    plt.show()
    # seaborn
    sns.boxplot(x=df_iris["Species"], y=df_iris['SepalWidth'])
    plt.title("鸢尾花类别和花瓣宽度箱线图")
    plt.show()
    # 6. 散点图
    # matplotlib
    plt.title("鸢尾花萼片和花瓣长宽散点图")
    plt.scatter(SepalLength, SepalWidth, label='萼片')
    plt.scatter(PetalLength, PetalWidth, label='花瓣')
    plt.xlabel("长度/(cm)")
    plt.ylabel("宽度/(cm)")
    plt.legend(loc="best")
    plt.show()
    # seaborn
    sns.scatterplot(x="SepalLength", y="SepalWidth", data=df_iris)
    sc = sns.scatterplot(x="PetalLength", y="PetalWidth", data=df_iris)
    plt.xlabel("长度")
    plt.ylabel("宽度")
    sc.set_title("鸢尾花花瓣萼片长宽散点图")
    plt.show()

    # 7. 回归图
    # matplotlib
    # 散点
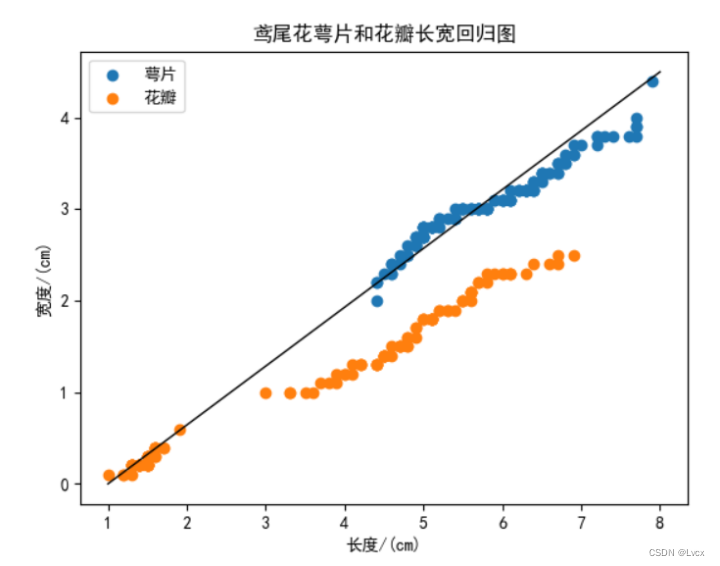
    plt.title("鸢尾花萼片和花瓣长宽回归图")
    plt.scatter(SepalLength, SepalWidth, label='萼片')
    plt.scatter(PetalLength, PetalWidth, label='花瓣')
    plt.xlabel("长度/(cm)")
    plt.ylabel("宽度/(cm)")
    plt.legend(loc="best")
    # 回归线
    plt.plot([1, 8], [0, 4.5], color="black", linewidth=1, label="回归线")
    plt.show()
    # seaborn
    # 散点
    sns.scatterplot(x="SepalLength", y="SepalWidth", data=df_iris)
    sc = sns.scatterplot(x="PetalLength", y="PetalWidth", data=df_iris)
    sc.set_title("鸢尾花花瓣萼片长宽回归图")
    # 回归线
    sns.regplot(x="SepalLength", y="SepalWidth", data=df_iris)
    plt.xlabel("长度")
    plt.ylabel("宽度")
    plt.show()


if __name__ == "__main__":
    main()


# 参考：https://blog.csdn.net/qinzhongyuan/article/details/106434854
# 选取指定行或列：https://zhuanlan.zhihu.com/p/76241647

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/490501.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Ae：橡皮擦工具

Ae：橡皮擦工具

橡皮擦工具 Eraser Tool 快捷键&#xff1a;Ctrl B 橡皮擦工具 Eraser Tool在工作原理上同 Ae 中的其它绘画工具&#xff08;画笔、仿制图章&#xff09;工具基本一致&#xff0c;都是通过绘制路径&#xff0c;然后基于此路径进行描边&#xff08;可统称为“绘画描边”&…
阅读更多...
黑马在线教育数仓实战9

黑马在线教育数仓实战9

2.6 数据清洗转换操作 ​ 目的: 主要是用于从ODS以及DIM层 将数据灌入到DWM层操作 生成学生出勤状态信息表 涉及表: course_table_upload_detail: 日志课程明细表 (课表) (维度表) tbh_student_signin_record: 学生打卡记录表 (事实表) tbh_class_time_ta…
阅读更多...
Windows下的RabbitMq安装（图文教学）

Windows下的RabbitMq安装（图文教学）

目录 前言一、安装Erlang1、下载地址&#xff1a; https://www.erlang.org/downloads2、安装3、配置环境变量4、测试安装 二、安装RabbitMq1、下载2、安装3、常用命令 参考 前言 RabbitMQ服务端代码是使用并发式语言Erlang编写的&#xff0c;安装Rabbit MQ的前提是安装Erlang …
阅读更多...
Visual Studio Code 1.78 发布

Visual Studio Code 1.78 发布

VS Code 1.78 已发布&#xff0c;此版本一些主要亮点包括&#xff1a; 辅助功能改进 - 更好的屏幕阅读器支持、新的音频提示。新的颜色主题 - “Modern” 浅色和深色主题默认设置。 配置文件模板 - Python、Java、数据科学等的内置模板。 新版本提供了配置文件模板&#xff0…
阅读更多...
Android网络代理原理及实现

Android网络代理原理及实现

网络代理简介 代理典型的分为三种类型&#xff1a; 正向代理 缓存服务器使用的代理机制最早是放在客户端一侧的&#xff0c;是代理的原型&#xff0c;称为正向代理。其目的之一 是缓存&#xff0c;另一目的是用来实现防火墙&#xff08;阻止互联网与公司内网之间的包&#x…
阅读更多...
AI 工具合辑盘点（六）持续更新

AI 工具合辑盘点（六）持续更新

AI 图像生成和编辑工具 不久前&#xff0c;艺术创作是特定群体的领域。 不再是这样了&#xff01; 今天&#xff0c;在人工智能艺术生成器的帮助下&#xff0c;任何人都可以通过编写文本提示并让人工智能创建所需的图像来成为艺术家。 &#x1f3a8;&#x1f58c; 文本到图像…
阅读更多...
多线程 双重检查锁详解

多线程 双重检查锁详解

&#x1f353; 简介&#xff1a;java系列技术分享(&#x1f449;持续更新中…&#x1f525;) &#x1f353; 初衷:一起学习、一起进步、坚持不懈 &#x1f353; 如果文章内容有误与您的想法不一致,欢迎大家在评论区指正&#x1f64f; &#x1f353; 希望这篇文章对你有所帮助,欢…
阅读更多...
Word处理控件Aspose.Words功能演示：在 Java 中将 Word DOC/DOCX 转换为 PDF

Word处理控件Aspose.Words功能演示：在 Java 中将 Word DOC/DOCX 转换为 PDF

Aspose.Words是一种高级Word文档处理API&#xff0c;用于执行各种文档管理和操作任务。API支持生成&#xff0c;修改&#xff0c;转换&#xff0c;呈现和打印文档&#xff0c;而无需在跨平台应用程序中直接使用Microsoft Word。 Aspose API支持流行文件格式处理&#xff0c;并…
阅读更多...
工业路由器误按RST复位键如何处理？RST键的作用

工业路由器误按RST复位键如何处理？RST键的作用

接触过工业路由器的朋友们都知道&#xff0c;几乎市面上的所有路由器产品都具备着一个常见但不常用的RST按键&#xff0c;它的作用是让工业路由器恢复出厂设置&#xff0c;也称为“复位键”“重置键”&#xff0c;用户可在通电情况下长按RST键10秒便会出现工业路由器指示灯全灭…
阅读更多...
高级【IO】

高级【IO】

目录 一.五种IO模型 &#xff08;1&#xff09;阻塞IO&#xff1a; &#xff08;2&#xff09;非阻塞IO &#xff08;3&#xff09;信号驱动IO: &#xff08;4&#xff09;IO多路转接 &#xff08;5&#xff09;异步IO 二.高级IO概念 1.同步通信、异步通信 2.阻塞、非阻…
阅读更多...
你知道ChatGPT里面的G、P、T分别代表什么吗？

你知道ChatGPT里面的G、P、T分别代表什么吗？

生成式AI&#xff0c; 在学习归纳数据分布的基础上&#xff0c;创造数据中不存在的新内容。可以生成文本、图片、代码、语音合成、视频和3D模型。 比尔盖茨&#xff1a;ChatGPT是1980年以来最具革命性的科技进步。 身处这个AI变革的时代&#xff0c;唯有躬身入局&#xff0c;…
阅读更多...
vcs -libmap

vcs -libmap

1 libmap的作用 主要两个作用: 解决module名重复问题: 比如有两个IP, IP0和IP1, 它们都例化了一个叫ADD的module, 而且它们的filelist中都包含add.v. 这时会引起编译错误, 这时可以: (1) 指定IP0中的add.v编译到库lib0中, IP1中的add.v编译到库lib1中, (2) 指定IP0中的ADD使用…
阅读更多...
超细Redis（二）

超细Redis（二）

五大数据类型 官方文档&#xff1a; 翻译&#xff1a; Redis 是一个开源&#xff08;BSD 许可&#xff09;内存数据结构存储系统&#xff0c;用作数据库、缓存、消息代理和流引擎。Redis 提供数据结构&#xff0c;例如字符串、哈希、列表、集、带有范围查询的排序集、位图、超…
阅读更多...
MySQL: 运算符使用练习

MySQL: 运算符使用练习

前言&#xff1a; 练习运算符的使用&#xff0c;加强记忆。 案例目的&#xff1a; 在已建数据库中创建数据表&#xff0c;并对表中数据进行处理&#xff0c;练习运算符&#xff08;包括数据运算符、逻辑运算符、位运算符&#xff09;的使用。 操作过程&#xff1a; 创建名…
阅读更多...
java基础入门-03-【字符串】

java基础入门-03-【字符串】

Java基础入门-03-【字符串】 10、字符串10.1.API10.1.1API概述10.1.2如何使用API帮助文档 10.2.String类10.2.1 String类概述10.2.2 String类的特点10.2.3 String类的构造方法10.2.4 创建字符串对象两种方式的区别10.2.5 字符串的比较10.2.5.1 号的作用10.2.5.2 equals方法的作…
阅读更多...
清华发布首个最全大模型安全评测系统，ChatGPT登榜首！

清华发布首个最全大模型安全评测系统，ChatGPT登榜首！

夕小瑶科技说 原创作者 | 天于刀刀 Python当前大型语言模型的火爆程度我们不用再进行赘述了&#xff0c;伴随着百度文心一言打响国内商业大模型第一枪&#xff0c;华为盘古&#xff0c;阿里通义千问&#xff0c;智谱ChatGLM,科大讯飞星火等国内公司纷纷开始布局。 另一方面由于…
阅读更多...
01-Flink Metrics简介

01-Flink Metrics简介

Flink Metrics简介 Flink Metrics是Flink集群运行中的各项指标&#xff0c;包含机器系统指标&#xff0c;比如&#xff1a;CPU、内存、线程、JVM、网络、IO、GC以及任务运行组件&#xff08;JM、TM、slot、作业、算子&#xff09;等相关指标。 Flink Metrics包含两大作用&…
阅读更多...
阿里云服务器购买教程（新手入门指南）

阿里云服务器购买教程（新手入门指南）

阿里云服务器ECS选购指南&#xff0c;阿里云百科分享2023阿里云服务器新手选择流程&#xff0c;选购云服务器有两个入口&#xff0c;一个是选择活动机&#xff0c;只需要选择云服务器地域、系统、带宽即可&#xff1b;另一个是在云服务器页面&#xff0c;自定义选择云服务器配置…
阅读更多...
探究C语言数组的奥秘：大小可省略的定义、内存存储、数组名、传参、指针遍历、数组指针和指针数组、柔性数组等

探究C语言数组的奥秘：大小可省略的定义、内存存储、数组名、传参、指针遍历、数组指针和指针数组、柔性数组等

也许你认为&#xff0c;C语言中的数组非常好理解&#xff0c;就是把一组相同类型的元素存储在同一块空间里。但是你可能并没有真正理解数组的本质&#xff0c;不信的话请回答一下下面的几个小问题&#xff0c;如果你能非常清晰的回答这些问题&#xff0c;那么你对C语言中的数组…
阅读更多...
【Git】制造冲突以及解决冲突的详细方法

【Git】制造冲突以及解决冲突的详细方法

介绍 这里是小编成长之路的历程&#xff0c;也是小编的学习之路。希望和各位大佬们一起成长&#xff01; 以下为小编最喜欢的两句话&#xff1a; 要有最朴素的生活和最遥远的梦想&#xff0c;即使明天天寒地冻&#xff0c;山高水远&#xff0c;路远马亡。 一个人为什么要努力&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023