1.图论入门
1.1存边方式
1.1.1 数组存边

1.1.2 临接矩阵存边

1.1.3 临接表存边


1.2 图的遍历和连通性
通过DFS和BFS遍历每一个图
对于非连通图,循环对每一个点dfs操作
也可以通过并查集来判断连通性
1.2.1全球变暖例题

import sys
sys.setrecursionlimit(60000) # 设置最大递归深度,默认递归深度有点小,不设置递归会出问题
def dfs(x,y):
d=[(-1,0),(0,1),(1,0),(0,-1)] # 左 上 右 下
global flag
vis[x][y] =1
if mp[x][y+1]=='#' and mp[x][y-1] =='#' and mp[x+1][y]=='#' and mp[x-1][y]=='#':
# 说明点(x,y)四周都是陆地
flag = 1 # 高地标记,不会被淹没
for i in range(4):
nx=x+d[i][0]
ny=y+d[i][1]
if vis[nx][ny] ==0 and mp[nx][ny] =='#':
# 如果当前没有遍历点(nx,ny)同时地图上面该点不是陆地
dfs(nx,ny)
n=int(input())
mp = [] # 记录地图
for i in range(n):
mp.append(list(input()))
vis =[] # 判断是否走过
for i in range(n):
vis.append([0]*n)
ans =0
for i in range(n): # 遍历每一点
for j in range(n):
if vis[i][j] ==0 and mp[i][j] =='#': # 相当于找连通分量
flag = 0
dfs(i,j)
if flag==0:
ans+=1
print(ans)
1.3 欧拉路和欧拉回路

哈密顿回路:图中每个点通过且只通过一次
1.3.1欧拉路和欧拉回路判定
无向图
如果图中的点全都是偶点,则存在欧拉回路;任意一点都可以作为起点和终点。
如果只有2个奇点,则存在欧拉路,其中一个奇点是起点,另一个是终点。不可能出现有奇数个奇点的无向图。
有向图
把一个点上的出度记为1,入度记为 -1,这个点上所有出度和入度相加,就是它的度数。
一个有向图存在欧拉回路,当且仅当该图所有点的度数为零。
如果只有一个度数为1的点,一个度数为-1的点,其它所有点的度数为0,那么存在欧拉路径,其中度数为1的是起点,度数为–1的是终点。
1.3.2 欧拉路劲例题

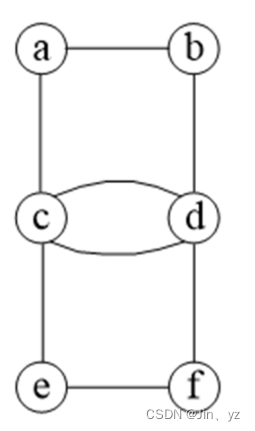
## 不全,没看懂
import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
def dfs(u):
i=d[u] # 从点u的第一条边i=0开始
while(i<len(G[u])):
d[u]=i+1 # 后面继续走u的下一条边
dfs(G[u][i]) # 继续走这条边的邻居点
i=dp[u] # 第i条边走过了,不再重复走
rec.append(u)
M=100100
n,m = map(int,input().split()) # n个点,m条边
du=[[0 for _ in range(2)] for _ in range(M)] # 记录入度,出度
G=[[] for _ in range(n+1)] # 临接表存图
d=[0 for _ in range(M)] # d[u]=i : 当前走u的第i个边
rec=[] #记录欧拉路
for i in range(m):
u,v =map(int,input().split())
G[u].append(v)
du[u][1]+=1 #出度
du[v][0]+=1 #入度
for i in range(1,n+1):
G[i].sort() # 对邻居点排序,字典序
S=1
2.Floyd算法
2.1 Floyd介绍

算法对比


2.2算法模板
import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
def floyd():
for k in range(1,n+1):
for i in range(1,n+1):
for j in range(1,n+1):
if dp[i][k]+dp[k][j] <dp[i][j]:
dp[i][j]=dp[i][k]+dp[k][j] 2.3 算法总结


2.4 算法例题
2.4.1 蓝桥公园

import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
def floyd():
for i in range(1,n+1):
for j in range(1,n+1):
for k in range(1,n+1):
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
n,m,q = map(int,input().split())
inf=2**120 #自定义无穷大
dp=[[inf]*(n+1) for i in range(n+1)] # 初始为无穷大
choice=[]
for i in range(m):
u,v,w=map(int,input().split()) # 无向图,临接矩阵存边
dp[u][v]=w
dp[v][u]=w
for i in range(q): # 读 起点和终点
s,d = map(int,input().split())
choice.append((s,d))
floyd()
for s,d in choice:
if dp[s][d]!=inf:
print(dp[s][d])
continue
print(-1)
2.4.2 路径

标准的floyd算法
import sys
import collections
import itertools
import heapq
import math
sys.setrecursionlimit(300000)
# 标准的floyd
def lcm(x,y): # 求最下公倍数
return x//math.gcd(x,y)*y
def floyd():
for k in range(1,2022):
for i in range(1,2022):
for j in range(1,2022):
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
dp=[[int(0x3f3f3f3f3f3f3f) for _ in range(2022)] for _ in range(2022)]
for i in range(1,2022):
for j in range(1,2022):
if abs(i-j)<=21: # 题意中的如果两个结点的差的绝对值不大于21
dp[i][j]=lcm(i,j)
print(dp[1][2021]
简化版Floyd算法
import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
import math
def lcm(i,j):
return i//math.gcd(i,j)*j
dp=[[2**50]*2022 for i in range(2022)]
# 创建图
for i in range(1,2022):
for j in range(i,2022):
if abs(i-j)<=21:
dp[i][j]=lcm(i,j)
# 找最短路径
for k in range(1,2022):
for i in range(1,2):
for j in range(1,2022):
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
print(dp[1][2021]) # 1026837
Bellman-Ford算法
import sys
import collections
import itertools
import heapq
import math
sys.setrecursionlimit(300000)
# Bellman_Ford算法
def lcm(x,y): # 求最下公倍数
return x//math.gcd(x,y)*y
dp=[int(0x3f3f3f3f3f3f3f) for _ in range(2022)]
for i in range(1,2022):
for j in range(i+1,i+22): # 题意中的如果两个结点的差的绝对值不大于21
if j>2021: break
dp[j]=min(dp[j],dp[i]+lcm(i,j)) # 更新最短路
print(dp[2021])
3.Dijstra算法
3.1 算法简介


3.2算法举例





3.3 例题模板
3.3.1 蓝桥王国

import sys
import collections
import itertools
import heapq # 默认小顶堆
import math
sys.setrecursionlimit(300000)
def dij(s):
vis=[0 for i in range(n+1)] # 标志是否访问过
hp=[] # 堆
dis[s]=0 # 自身到自身的距离为0
heapq.heappush(hp,(0,s)) # 列表堆化同时入堆
while hp:
u=heapq.heappop(hp)[1] # 出堆,出的是结点
if vis[u]: # 判断是否处理过
continue
vis[u]=1
for i in G[u]:
v,w=i[0],i[1]
if vis[v]:
continue
if dis[v]>dis[u]+w:
dis[v]=dis[u]+w
heapq.heappush(hp,(dis[v],v))
n,m=map(int,input().split())
s=1
G=[[]for i in range(n+1)] # 临接表存图
inf=2**64
dis=[inf]*(n+1) # 从1到其他点的距离
for i in range(m): # 邻接表存m条边
u,v,w=map(int,input().split())
G[u].append((v,w))
dij(s) # 以s为起点到其他点的最短路径
for i in range(1,n+1):
if dis[i]>=inf :
print("-1",end=' ')
else:
print(dis[i],end=" ")
3.3.2 矩阵矩阵形式的Dijstra模板



import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)
def dij():
dist[1]=0 #很重要
for _ in range(n-1): # 还有n-1个点没有遍历
t=-1
for j in range(1,n+1):
if st[j]==0 and (t==-1 or dist[t]>dist[j]): #找到没处理过得最小距离点
t=j
for j in range(1,n+1):
dist[j]=min(dist[j],dist[t]+gra[t][j]) # t-j的距离,找最小值
st[t]=1 # 标记处理过
return dist[n]
n,m=map(int,input().split())
#下标全部转为从1开始
stay=[0]+list(map(int,input().split()))
stay[n]=0
gra = [[float('inf')] * (n+1) for _ in range(n+1)]
dist = [float('inf')] * (n+1)
st=[0]*(n+1) # 标志是否处理
for i in range(m):
u,v,w=map(int,input().split()) #这里重构图
gra[u][v]=stay[v]+w
gra[v][u]=stay[u]+w
print(dij())
4.Bellman-Ford算法
4.1 算法简介
单源最短路径问题:给定一个起点s,求它到图中所有n个结点的最短路径。

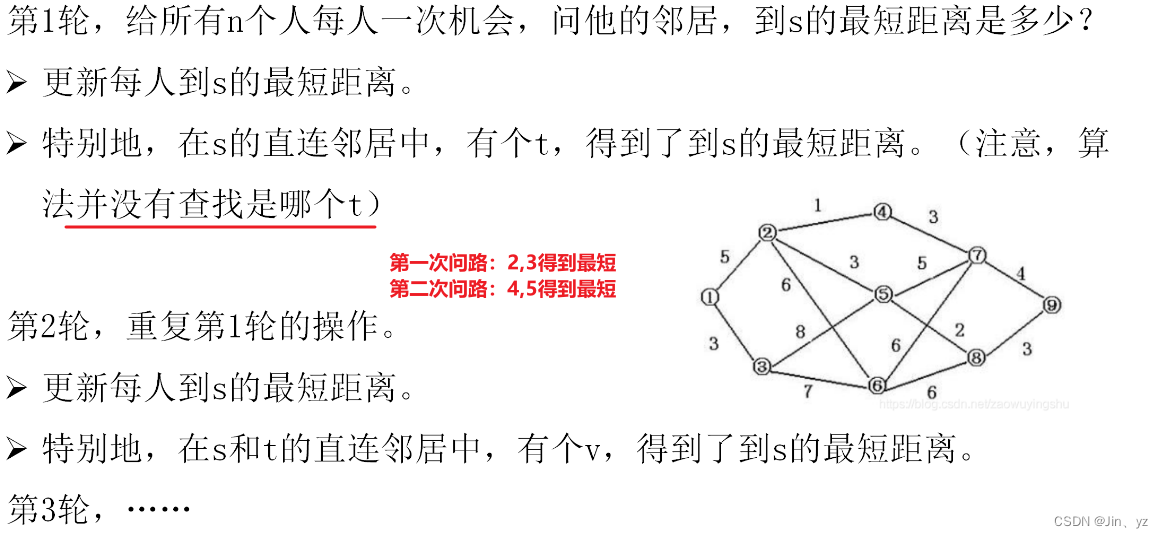


4.2 算法模板和例题
4.2.1 出差问题

Bellman——Ford实现
import sys
import collections
import itertools
import heapq # 默认小顶堆
import math
sys.setrecursionlimit(300000)
n,m = map(int,input().split())
t=[0]+list(map(int,input().split())) # 从t=1开始
e=[] # 数组存边
for i in range(1,m+1):
a,b,c = map(int,input().split())
e.append([a,b,c])
e.append([b,a,c]) # 双向边
dist=[2**64]*(n+1) # 存储到终点的距离
dist[1]=0
for k in range(1,n+1): # 最大循环n次,即n个点
for a,b,c in e: # 检查每条边
res=t[b] # b的隔离时间
if b==n:
res=0
dist[b]=min(dist[b],dist[a]+c+res) # 问邻居是否能到达起点
print(dist[n])Dijstra实现
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)
def dij():
dist[1]=0 #很重要
for _ in range(n-1): # 还有n-1个点没有遍历
t=-1
for j in range(1,n+1):
if st[j]==0 and (t==-1 or dist[t]>dist[j]): #找到没处理过得最小距离点
t=j
for j in range(1,n+1):
dist[j]=min(dist[j],dist[t]+gra[t][j]) # t-j的距离,找最小值
st[t]=1 # 标记处理过
return dist[n]
n,m=map(int,input().split())
#下标全部转为从1开始
stay=[0]+list(map(int,input().split()))
stay[n]=0
gra = [[float('inf')] * (n+1) for _ in range(n+1)]
dist = [float('inf')] * (n+1)
st=[0]*(n+1) # 标志是否处理
for i in range(m):
u,v,w=map(int,input().split()) #这里重构图
gra[u][v]=stay[v]+w
gra[v][u]=stay[u]+w
print(dij())
5.SPFA算法
5.1 算法简介
改进的Bellman-Ford算法

5.2 算法步骤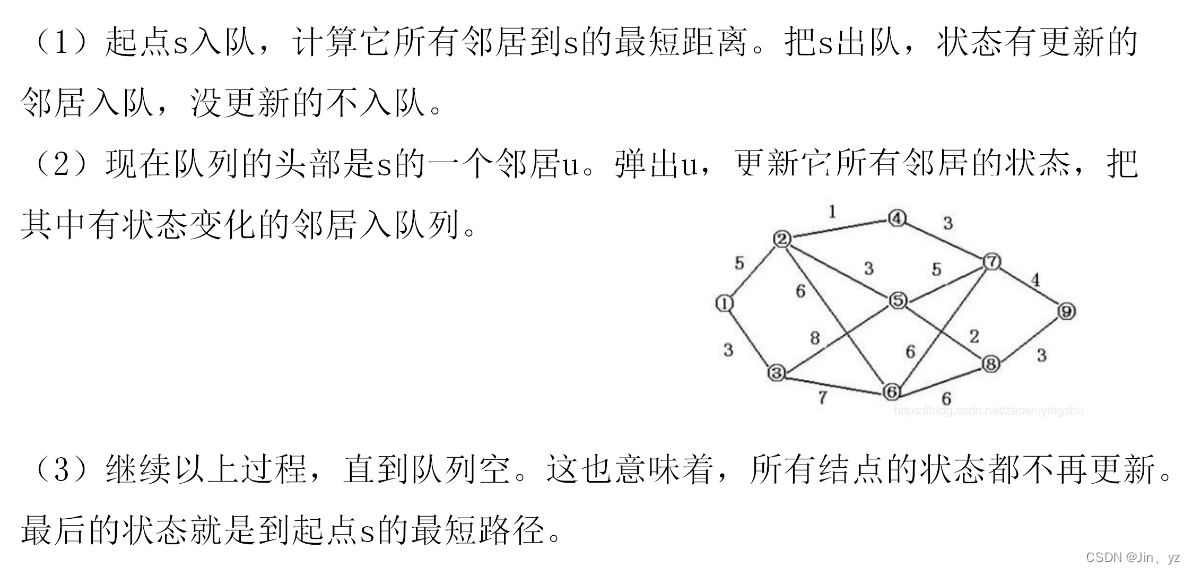
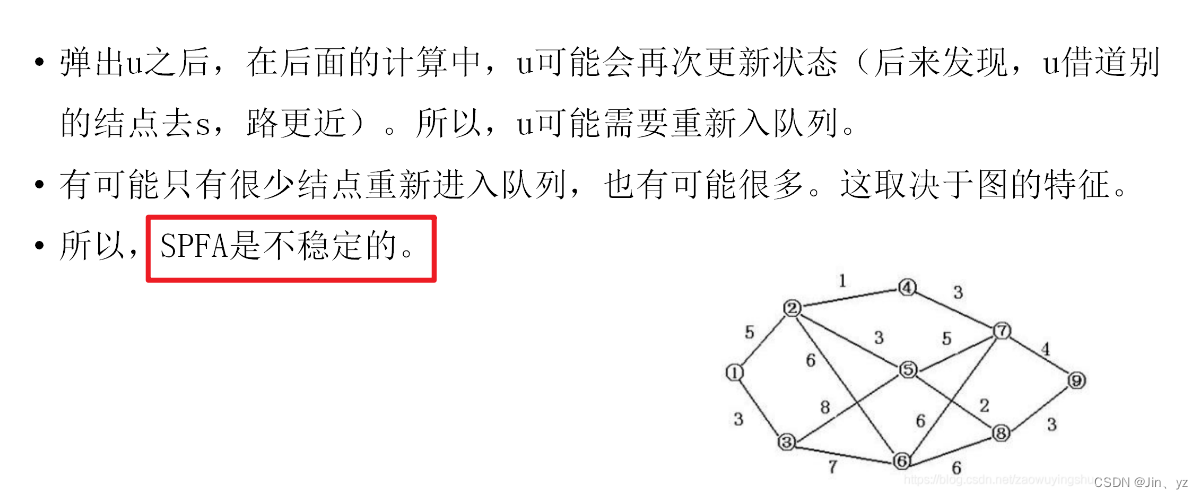
5.3 算法例题和模板
5.3.1 随机数据下的最短路问题

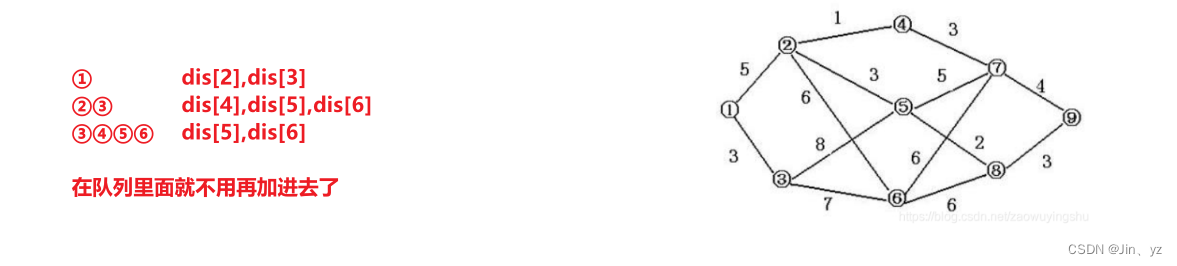
import sys
import collections
import itertools
import heapq # 默认小顶堆
import math
sys.setrecursionlimit(300000)
def spfa(s):
dis[s]=0
hp=[]
heapq.heappush(hp,s)
inq=[0]*(n+1) # 判断是否在队列中
inq[s]=1
while(hp):
u=heapq.heappop(hp)
inq[u]=0
''' 下面两句认为没用,因为队列中的u都是因为上一个结点的邻居更新后
放进来的,删了之后一样AC '''
if dis[u]==inf: #到起点的距离为无穷大,没有必要更新邻居
continue
for v,w in e[u]: # 遍历u的邻接表
if dis[v]>dis[u]+w:
dis[v]=dis[u]+w
if(inq[v]==0): # 状态有更新,v的邻居可以通过他得到更近路径
heapq.heappush(hp,v)
inq[v]=1
n,m,s = map(int,input().split())
e=[[] for i in range(n+1)] # 临接表存边
inf=2**64
dis=[inf]*(n+1)
for i in range(m): # 读边
u,v,w = map(int,input().split())
e[u].append((v,w)) # 邻接表存边,有向图
spfa(s)
for i in range(1,n+1):
if dis[i]>=inf:
print('-1',end=' ')
else:
print(dis[i],end=' ')
5.4 Dijstra和SPFA对比


6.最小生成树算法
6.1 Prim算法
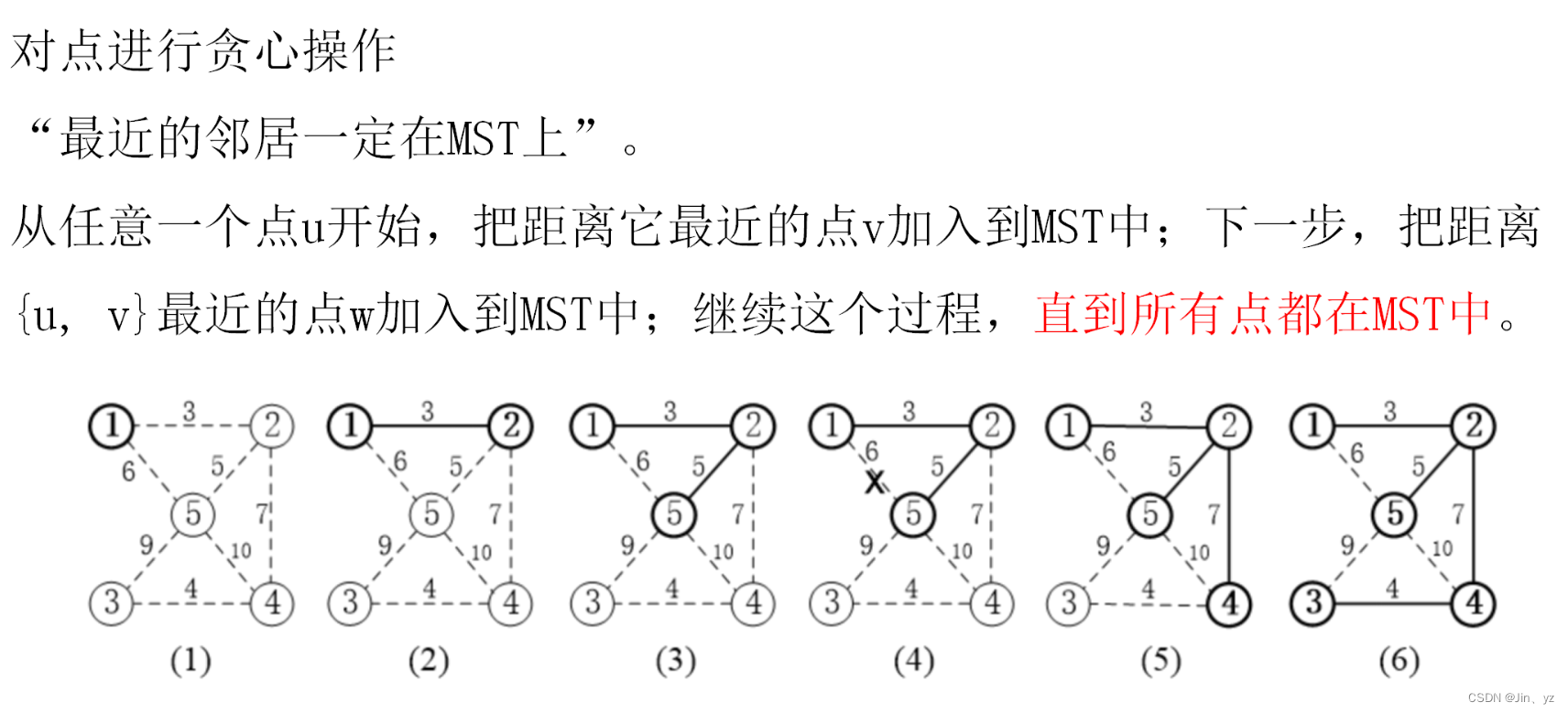
6.1.1 修建公路(例题模板)

import sys
import collections
import itertools
import heapq # 默认小顶堆
import math
sys.setrecursionlimit(300000)
def prim():
ans,cnt=0,0 # cnt 是加入MST的点的数量
q=[]
vis=[0 for i in range(n+1)] # 1 表示点在MST中
heapq.heappush(q,(0,1))
while q and cnt<n:
w,u = heapq.heappop(q) # 出距离集合最近的点
if vis[u] !=1: # 不再MST中
vis[u]=1
ans+=w
cnt+=1
for v,w in e[u]: # 遍历点u的邻居,边长为w
heapq.heappush(q,[w,v]) # 加入MST的点的数量不等于n,说明原图不连通
if cnt!=n: # 加入MST的点的数量不等于n,说明原图不连通
print('-1')
else:
print(ans)
n,m = map(int,input().split())
e=[[] for i in range(n+1)]
for i in range(m):
u,v,w =map(int,ipnut().split())
e[u].append((v,w)) # u的邻居是v,边长w
e[v].append((u,w)) # 双向边
prim()
6.2 Krusal算法

通过并查集实现
6.2.1 例题模板(修建公路)

import sys
import collections
import itertools
import heapq # 默认小顶堆
import math
sys.setrecursionlimit(300000)
def find(x):
if s[x] ==x:
return x
s[x]=find(s[x]) # 路径压缩
return s[x]
def merge(x,y):
s[find(y)]=find(x)
def kruskal():
cnt=0
ans=0
e.sort(key=lambda x: x[2]) # 将边从小到大排序
for i in range(n+1): # 并查集初始化
s.append(i)
for i in range(m): # 遍历所有边
x,y=e[i][0],e[i][1]
e1,e2 =find(x),find(y)
if e1==e2: # 属于同一个集,要这条边的话产生圈
continue
else:
ans+=e[i][2]
merge(x,y)
cnt+=1
if cnt==n-1:
break
if cnt!=n-1: # 边的数量不等于n-1,说明有点不再MST上面
print(-1)
else:
print(ans)
return
e=[] # 数组存边
s=[] # 并查集
n,m=map(int,input().split())
for i in range(m): # 存m条边
u,v,w = map(int,input().split())
e.append((u,v,w)) # 存边
kruskal()
6.3 两种算法对比