什么是SVM?
VM的英文全称是Support Vector Machines,我们叫它支持向量机。支持向量机是我们用于分类的一种算法。让我们以一个小故事的形式,开启我们的SVM之旅吧。
在很久以前的情人节,一位大侠要去救他的爱人,但天空中的魔鬼和他玩了一个游戏。
魔鬼在桌子上似乎有规律放了两种颜色的球,说:“你用一根棍分开它们?要求:尽量在放更多球之后,仍然适用。”
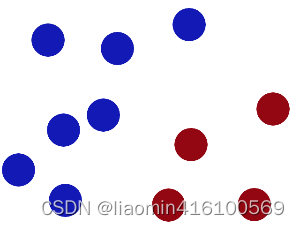
于是大侠这样放,干的不错?
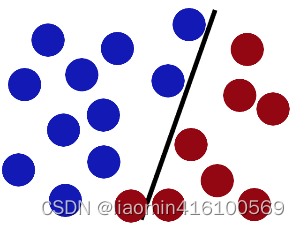
然后魔鬼,又在桌上放了更多的球,似乎有一个球站错了阵营。显然,大侠需要对棍做出调整。

SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙。这个间隙就是球到棍的距离。
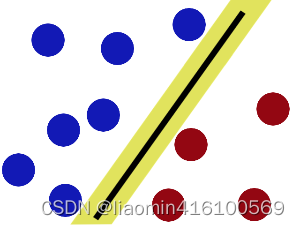
现在好了,即使魔鬼放了更多的球,棍仍然是一个好的分界线。
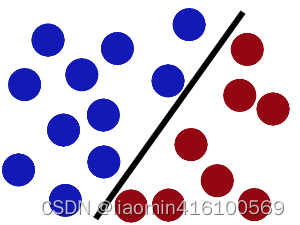
现在,大侠没有棍可以很好帮他分开两种球了,现在怎么办呢?当然像所有武侠片中一样大侠桌子一拍,球飞到空中。然后,凭借大侠的轻功,大侠抓起一张纸,插到了两种球的中间。
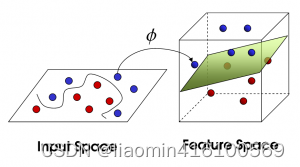
现在,从空中的魔鬼的角度看这些球,这些球看起来像是被一条曲线分开了。
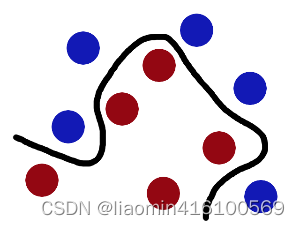
再之后,无聊的大人们,把这些球叫做data,把棍子叫做classifier, 找到最大间隙的trick叫做optimization,拍桌子叫做kernelling, 那张纸叫做hyperplane。
概述一下:
当一个分类问题,数据是线性可分的,也就是用一根棍就可以将两种小球分开的时候,我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可,寻找这个最大间隔的过程,就叫做最优化。但是,现实往往是很残酷的,一般的数据是线性不可分的,也就是找不到一个棍将两种小球很好的分类。这个时候,我们就需要像大侠一样,将小球拍起,用一张纸代替小棍将小球进行分类。想要让数据飞起,我们需要的东西就是核函数(kernel),用于切分小球的纸,就是超平面。
数学建模
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行广义线性分类,其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)。SVM可以通过核函数进行非线性分类,是常见的核学习(kernel learning)方法之一。
支持向量机(support vector machines)是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。它既能解决线性可分又能解决线性不可能,既能解决分类问题又能完成回归问题。
间隔最大化
当训练样本线性可分时使用硬间隔最大化(Hard Margin SVM)或者近似线性可分时使用软件最大化(Soft Margin SVM)。当训练样本线性不可分时使用核函数和软间隔最大化。
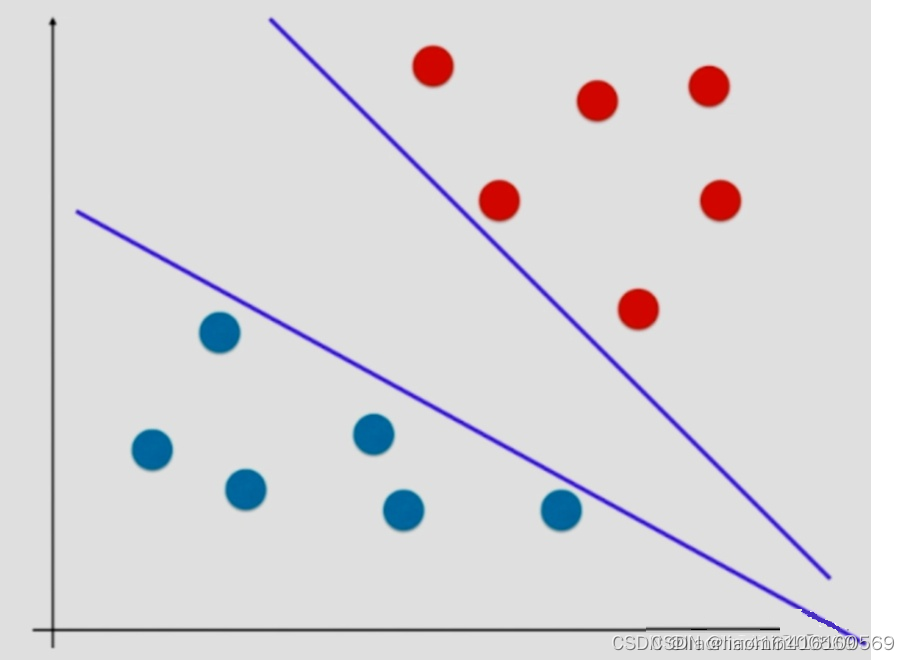
在实际问题中往往都存在着决策边界不唯一的情况,这就是不适定问题。给定训练样本集
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
…
,
(
x
m
,
y
m
)
}
,
y
i
∈
{
−
1
,
1
}
D = \{(x_{1}, y_{1}), (x_{2}, y_{2}), \dots , (x_{m}, y_{m})\}, y_{i} \in \{-1, 1\}
D={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{−1,1} 分类算法的基本思想就是基于训练集在样本空间中找到一个划分超平面,但是能将训练样本分开的划分超平面可能有很多,所以,应该努力地去找哪一个?
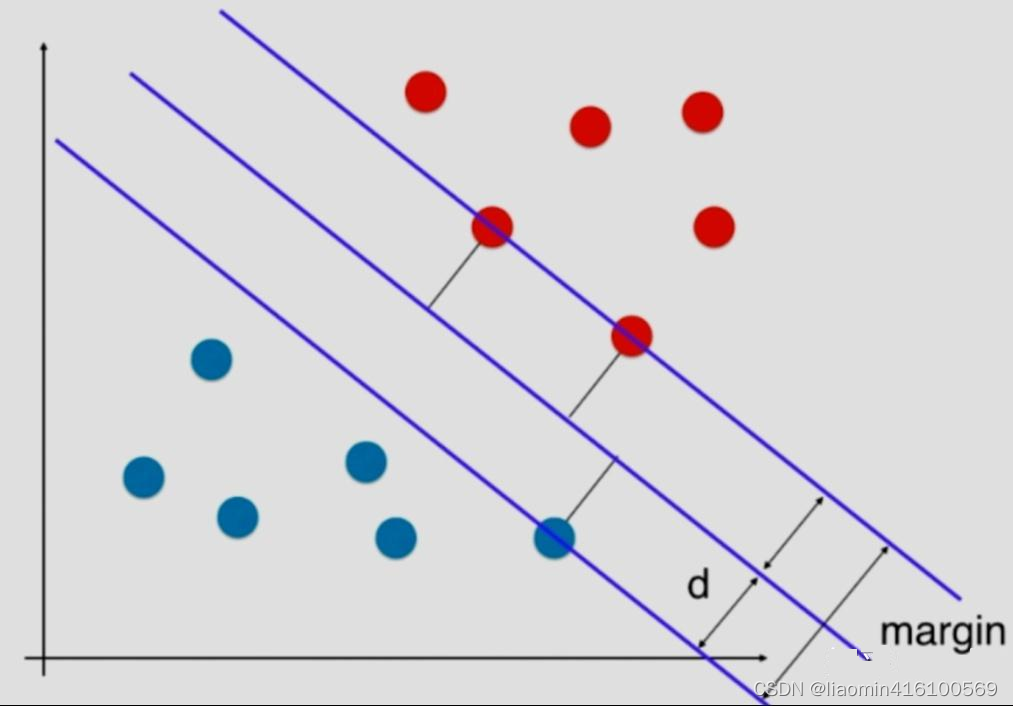
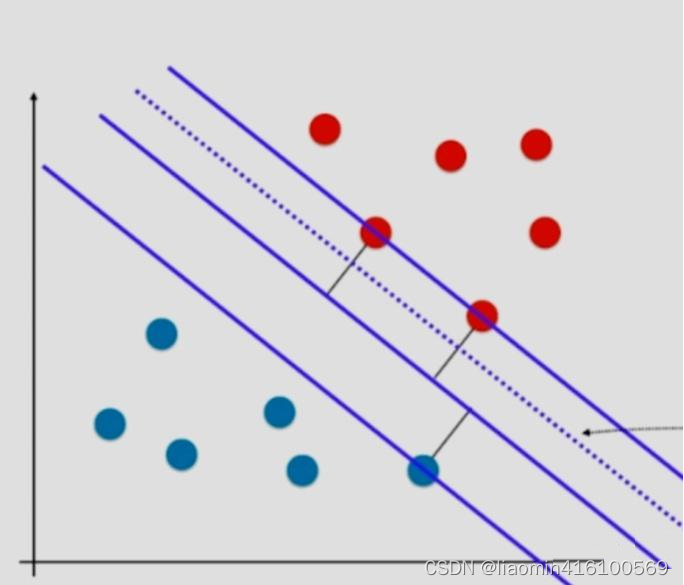
而svm找到的这条直线希望距离最近的红色的点和蓝色的点,距离决策边界尽可能的远,这样就能保证模型的泛化能力。svm尝试寻找一个最优的决策边界,距离两个类别最近的样本最远,图中3个点到决策边界距离相同。这三个点就叫做支持向量(support vector)。而平行于决策边界的两条直线之间的距离就是margin,svm就是要最大化 margin,这样就把这个问题转化称为最优化问题。
最优化问题
分类间隔方程
svm最大化margin,margin=2d,,就对应于最大化d,也就是点到直线的距离最大。回忆解析几何,在二维空间中点
(
x
,
y
)
(x,y)
(x,y)到直线
A
x
+
B
y
+
C
=
0
Ax+By+C=0
Ax+By+C=0的距离公式 :
∣
A
x
+
B
y
+
C
∣
A
2
+
B
2
\frac{\mid Ax+By+C \mid} {\sqrt{A^2+B^2}}
A2+B2∣Ax+By+C∣
将其拓展到n维
θ
T
⋅
x
b
=
0
\theta^T \cdot x_{b}=0
θT⋅xb=0
其中
θ
\theta
θ包含截距和系数,
x
b
x_b
xb就是在
x
x
x 样本中加入一行常数1,这就跟之前的线性回归中是一样的。
如果将截距提出来就是
w
T
x
+
b
=
0
w^Tx + b = 0
wTx+b=0
其中的w就是对样本中的每一个数据赋予了一个权值。这就是直线方程的两种不同表示方式。那么,由此可以得到新的点到直线距离方程:
∣
w
T
x
+
b
∣
∥
w
∥
\frac{\mid w^Tx + b \mid}{\parallel w \parallel}
∥w∥∣wTx+b∣,其中
∥
w
∥
=
w
1
2
+
w
2
2
+
⋯
+
w
n
2
\parallel w \parallel = \sqrt {w_{1}^2 + w_{2}^2 + \dots + w_{n}^2}
∥w∥=w12+w22+⋯+wn2
约束条件
看起来,我们已经顺利获得了目标函数的数学形式。但是为了求解w的最大值。我们不得不面对如下问题:
- 我们如何判断超平面是否将样本点正确分类?
- 我们知道要求距离d的最大值,我们首先需要找到支持向量上的点,怎么在众多的点中选出支持向量上的点呢?
上述我们需要面对的问题就是约束条件,也就是说我们优化的变量d的取值范围受到了限制和约束。事实上约束条件一直是最优化问题里最让人头疼的东西。但既然我们已经知道了这些约束条件确实存在,就不得不用数学语言对他们在这里插入图片描述
进行描述。但SVM算法通过一些巧妙的小技巧,将这些约束条件融合到一个不等式里面。
这个二维平面上有两种点,我们分别对它们进行标记:
红颜色的圆点标记为1,我们人为规定其为正样本;
蓝颜色的五角星标记为-1,我们人为规定其为负样本。
对每个样本点xi加上一个类别标签yi:

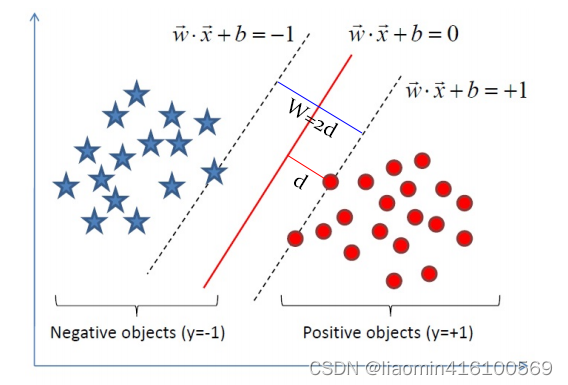
中间那根直线就是决策边界
w
T
x
+
b
=
0
w^Tx+b=0
wTx+b=0 ,而上下两根直线意味着距离一定大于 d ,从而
{
w
T
x
(
i
)
+
b
∥
w
∥
≥
d
∀
y
(
i
)
=
1
w
T
x
(
i
)
+
b
∥
w
∥
≤
−
d
∀
y
(
i
)
=
−
1
\begin {cases} \frac{w^Tx^{(i)} + b} {\parallel w \parallel} \geq d \qquad \forall y^{(i)} = 1 \\ \frac{w^Tx^{(i)} + b}{\parallel w \parallel} \leq -d \qquad \forall y^{(i)} = -1 \\ \end {cases}
{∥w∥wTx(i)+b≥d∀y(i)=1∥w∥wTx(i)+b≤−d∀y(i)=−1
此时,假设两类样本分别为1和-1。然后将上述式子的左右两侧同时除以d,得到
{
w
T
x
(
i
)
+
b
∥
w
∥
d
≥
1
∀
y
(
i
)
=
1
w
T
x
(
i
)
+
b
∥
w
∥
d
≤
−
1
∀
y
(
i
)
=
−
1
\begin {cases} \frac{w^Tx^{(i)} + b} {\parallel w \parallel d} \geq 1 \qquad \forall y^{(i)} = 1 \\ \frac{w^Tx^{(i)} + b}{\parallel w \parallel d} \leq -1 \qquad \forall y^{(i)} = -1 \\ \end {cases}
{∥w∥dwTx(i)+b≥1∀y(i)=1∥w∥dwTx(i)+b≤−1∀y(i)=−1
其中 |w|和 d都是一个标量(不影响求极限值),此时消去分母,得到
{
w
T
x
(
i
)
+
b
≥
1
∀
y
(
i
)
=
1
w
T
x
(
i
)
+
b
≤
−
1
∀
y
(
i
)
=
−
1
\begin {cases} {w^Tx^{(i)} + b} \geq 1 \qquad \forall y^{(i)} = 1 \\ {w^Tx^{(i)} + b} \leq -1 \qquad \forall y^{(i)} = -1 \\ \end {cases}
{wTx(i)+b≥1∀y(i)=1wTx(i)+b≤−1∀y(i)=−1
此时,就得到了两个式子,接下来通过一个小技巧将两个式子合并成一个。
y
i
(
w
T
x
(
i
)
+
b
)
≥
1
\boxed {y_{i} (w^Tx^{(i)} + b) \geq 1}
yi(wTx(i)+b)≥1
最大化目标函数
现在整合一下思路,我们已经得到我们的目标函数:
m
a
x
∣
w
T
x
+
b
∣
∥
w
∥
max \frac{\mid w^Tx +b \mid}{\parallel w \parallel}
max∥w∥∣wTx+b∣
我们的优化目标是是d最大化。我们已经说过,我们是用支持向量上的样本点求解d的最大化的问题的。那么支持向量上的样本点有什么特点呢?
∣
w
T
x
+
b
∣
=
1
|w^Tx+b|=1
∣wTx+b∣=1
所以转化为最大化
m
a
x
1
∥
w
∥
max \frac{1}{\parallel w \parallel}
max∥w∥1 也即是最小化
m
i
n
∥
w
∥
min\parallel w \parallel
min∥w∥
但是往往为了求导方便,通常都是最小化
m
i
n
1
2
∥
w
∥
2
\boxed{min\frac{1}{2} \parallel w \parallel^2}
min21∥w∥2
,但是这是一个有约束条件的最优化问题,就是要满足
s
.
t
.
y
i
(
w
T
x
(
i
)
+
b
)
≥
1
,
i
=
1
,
2
,
…
,
m
s.t. \quad y_{i} (w^Tx^{(i)} + b) \geq 1, \quad i=1,2,\dots,m
s.t.yi(wTx(i)+b)≥1,i=1,2,…,m
这里m是样本点的总个数,缩写s.t.表示"Subject to",是"服从某某条件"的意思。上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型。
解决有约束问题的最优化问题需要使用拉格朗日乘子法得到对偶问题。则该问题函数:
L
(
w
,
b
,
α
)
=
1
2
∥
w
∥
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
\boxed{L(w, b, \alpha) = \frac{1}{2} \parallel w \parallel^2 + \sum_{i=1}^m \alpha_{i} (1-y_{i}(w^Tx_{i}+b))}
L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(wTxi+b))
其中 α i \alpha_i αi 就是拉格朗日乘子。这就是Hard Margin SVM。
Soft Margin和SVM正则化
如果在实际应用过程中有一个蓝色的点出现在红色的点附近,即两类相对较为接近,但整体跟蓝色的点差异明显,可以看做是一个特殊点或者错误的奇点,此时就会误导,导致最终的hard margin分类边界是直线1,此时模型的泛化能力就值得怀疑。正常来说应该像直线2一样忽略那个极度特殊的蓝点,保证大多数的数据到直线的距离最远,可能这才是最好的分类边界,也就是泛化能力更高。这也能间接地说明如果模型的准确率过高可能会导致模型的过拟合。
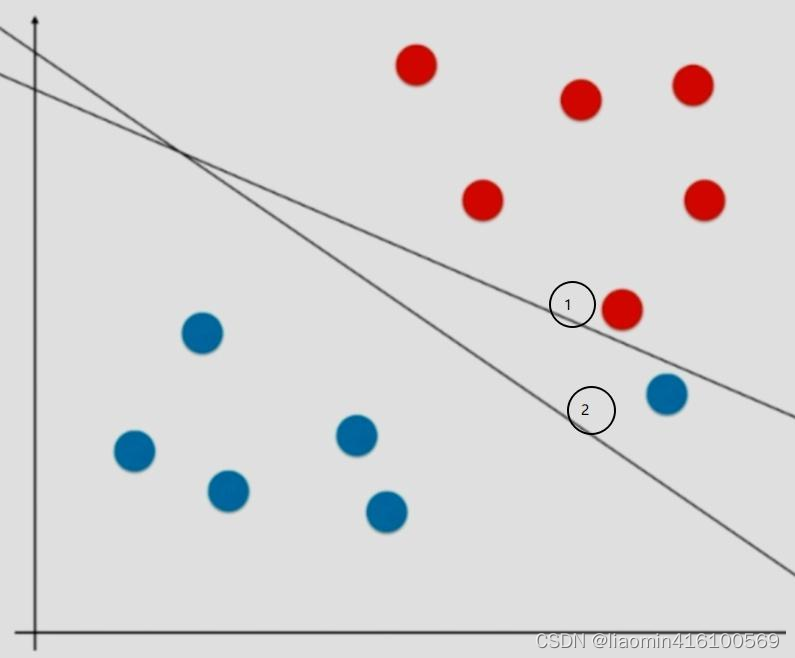
还有一种更一般的例子,那就是如果有一个蓝色的点混进了红色的点当中,这就导致数据集根本就是线性不可分的情况,根本找不出一条直线能够将这两类分开,在这种情况下Hard margin就不再是泛化能力强不强的问题,而是根本找不出一条直线将其分开。
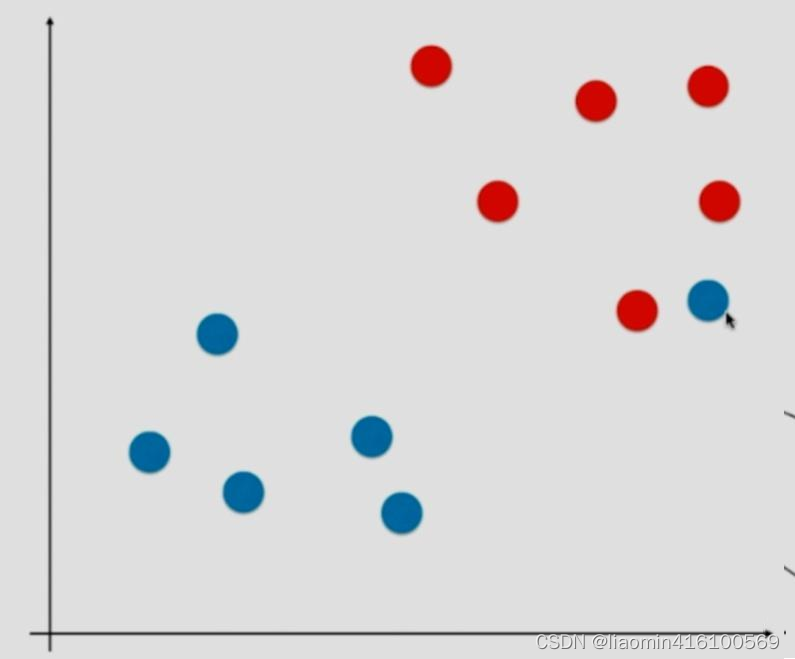
因此不管才以上两种情况的哪个角度出发,都应该考虑给予svm模型部分容错能力。由此引出Soft Margin SVM。
m
i
n
1
2
∥
w
∥
2
,
s
.
t
.
y
i
(
w
T
x
(
i
)
+
b
)
≥
1
−
ζ
i
,
ζ
i
>
0
,
i
=
1
,
2
,
…
,
m
min\frac{1}{2} \parallel w \parallel^2, \quad s.t. \quad y_{i} (w^Tx^{(i)} + b) \geq 1 - \zeta_{i}, \\ \quad \zeta_{i} >0, \quad i=1,2,\dots,m
min21∥w∥2,s.t.yi(wTx(i)+b)≥1−ζi,ζi>0,i=1,2,…,m
相比于Hard Margin SVM,就相当于把条件放得更加宽松一些,直观从图上理解,就是相当于把上面这根直线放宽到虚线。此外,更加重要的一点是
ζ
i
\zeta_{i}
ζi并不是一个固定值,而是相对应于每个样本
x
i
x_i
xi都有一个
ζ
i
\zeta_{i}
ζi,但是对于这个
ζ
i
\zeta_{i}
ζi也需要一定限制,并不是说可以无限放宽这个条件。也就是这个容错空间不能太大,因此需要对其加以限制。
L1正则
m
i
n
(
1
2
∥
w
∥
2
+
C
∑
i
=
1
m
ζ
i
)
,
s
.
t
.
y
i
(
w
T
x
(
i
)
+
b
)
≥
1
−
ζ
i
,
ζ
i
≥
0
,
i
=
1
,
2
,
…
,
m
\boxed { min(\frac{1}{2} \parallel w \parallel^2 +C \sum_{i=1}^m \zeta_{i}), \quad s.t. \quad y_{i} (w^Tx^{(i)} + b) \geq 1 - \zeta_{i}, \\ \qquad \qquad \qquad \qquad \zeta_{i} \geq 0, \quad i=1,2,\dots,m }
min(21∥w∥2+Ci=1∑mζi),s.t.yi(wTx(i)+b)≥1−ζi,ζi≥0,i=1,2,…,m
引入一个新的超参数C去权衡容错能力和目标函数,其实这也可以理解为我们为其加入了L1正则项,避免模型向一个极端方向发展,使得对于极端的数据集不那么敏感,对于未知的数据有更好的泛化能力。这个所谓的L1正则跟之前的L1正则不同的是没有绝对值,只是因为已经限制了
ζ
i
≥
0
\zeta_{i} \geq 0
ζi≥0,所以不加绝对值也就合理了。C越大越趋近于一个Hard Margin SVM,C越小,就意味着有更大的容错空间。svm的正则与线性回归的正则不同的是在于C的位置不同。具体原因后续理解更深刻之后再更新。
那么有L1正则,相对应就有L2正则,如下。
m
i
n
(
1
2
∥
w
∥
2
+
C
∑
i
=
1
m
ζ
i
2
)
,
s
.
t
.
y
i
(
w
T
x
(
i
)
+
b
)
≥
1
−
ζ
i
,
ζ
i
>
0
,
i
=
1
,
2
,
…
,
m
\boxed { min(\frac{1}{2} \parallel w \parallel^2 +C \sum_{i=1}^m \zeta_{i}^2), \quad s.t. \quad y_{i} (w^Tx^{(i)} + b) \geq 1 - \zeta_{i}, \\ \qquad \qquad \qquad \qquad \zeta_{i} >0, \quad i=1,2,\dots,m }
min(21∥w∥2+Ci=1∑mζi2),s.t.yi(wTx(i)+b)≥1−ζi,ζi>0,i=1,2,…,m
Sklearn的svm
在实际使用SVM的时候和KNN一样需要对数据进行标准化处理,因为这两者都涉及距离。因为当数据尺度相差过大的话,比如下图横轴0-1,纵轴0-10000。所以先进行标准化是必要的。
第一步,准备一个简单二分类数据集:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
"""
load_iris是一个经典的机器学习数据集,它包含了150个样本
这个数据集中的四个特征分别是花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)和花瓣宽度(petal width),
它们都是以厘米(cm)为单位测量的。目标变量是鸢尾花的种类,
有三种不同的种类:Setosa、Versicolour和Virginica。
它们的中文名分别是山鸢尾、杂色鸢尾和维吉尼亚鸢尾。
"""
iris = datasets.load_iris()
x = iris.data
y = iris.target
# 只做一个简单的二分类,获取分类是山鸢尾、杂色鸢尾的数据,同时取2维的特征就行了
x = x[y<2, :2]
y = y[y<2]
#分别绘制出分类是0和1的点,不同的scatter颜色不一样
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()
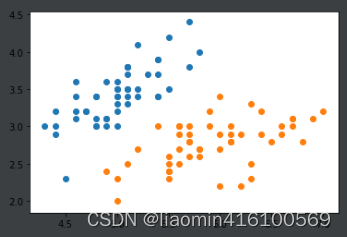
实现svm,先使用一个比较大的C。
# 标准化数据
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
#数据归一化
standardscaler = StandardScaler()
standardscaler.fit(x)
x_standard = standardscaler.transform(x)
svc = LinearSVC(C=1e9)
svc.fit(x_standard, y)
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1),)
x_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(x_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
w = model.coef_[0]
b = model.intercept_[0]
# w0*x0 + w1*x1 + b = 0
# x1 = -w0/w1 * x0 - b/w1
plot_x = np.linspace(axis[0], axis[1], 200)
up_y = -w[0]/w[1] * plot_x - b/w[1] + 1/w[1]
down_y = -w[0]/w[1] * plot_x - b/w[1] - 1/w[1]
up_index = (up_y >= axis[2]) & (up_y <= axis[3])
down_index = (down_y >= axis[2]) & (down_y <= axis[3])
plt.plot(plot_x[up_index], up_y[up_index], color='black')
plt.plot(plot_x[down_index], down_y[down_index], color='black')
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(x_standard[y==0, 0], x_standard[y==0, 1], color='red')
plt.scatter(x_standard[y==1, 0], x_standard[y==1, 1], color='blue')
plt.show()
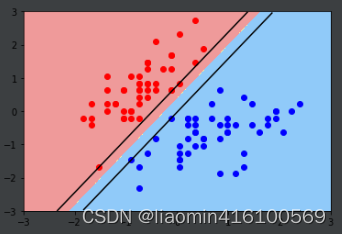
使用一个比较小的C,对比C取不同值的效果。
svc2 = LinearSVC(C=0.01)
svc2.fit(x_standard, y)
plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(x_standard[y==0, 0], x_standard[y==0, 1], color='red')
plt.scatter(x_standard[y==1, 0], x_standard[y==1, 1], color='blue')
plt.show()
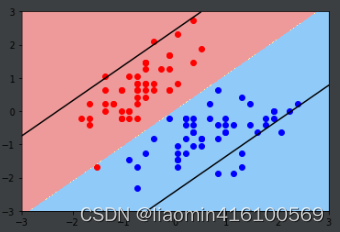
对比两幅图可以发现,当C较小时,误将一个红色的点分到蓝色当中,这也再次验证了当C越小,就意味着有更大的容错空间。
SVM中使用多项式特征
前面一直都在讲的是线性的svm,对于svm来说也可以解决非线性问题,类比线性回归到非线性回归的思想,首先使用多项式特征。
首先生成数据集:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x, y = datasets.make_moons()
x.shape
# (100, 2)
y.shape
# (100,)
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()
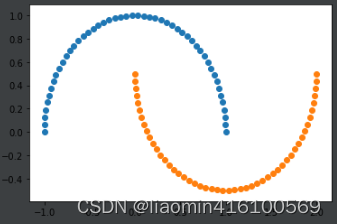
接下来给数据添加一些随机噪声:
x, y = datasets.make_moons(noise=0.15, random_state=666)
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()

使用多项式,归一,线性svm
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomiaSVC(degree, C=1.0):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('linear_svc', LinearSVC(C=C))
])
poly_svc = PolynomiaSVC(degree=3)
poly_svc.fit(x, y)
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1),)
x_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(x_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x1[y1==0, 0], x1[y1==0, 1])
plt.scatter(x1[y1==1, 0], x1[y1==1, 1])
plt.show()
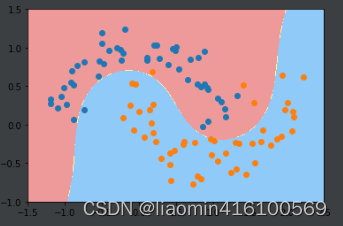
除了使用这种增加多项式特征之后再给入线性svc中之外,还有一种方法可以实现类似的功能。
from sklearn.svm import SVC
# 这种方法训练的过程并不完全是先将数据进行标准化,再使用linearSVC这么一个过程
# SVC中默认的C=0
def PolynomiaKernelSVC(degree, C=1.0):
return Pipeline([
('std_scale', StandardScaler()),
('kernel_svc', SVC(kernel='poly', degree=degree, C=C))
])
poly_kernel_svc = PolynomiaKernelSVC(degree=3)
poly_kernel_svc.fit(x1, y1)
# Pipeline(memory=None,
# steps=[('std_scale', StandardScaler(copy=True, with_mean=True, with_std=True)),
# ('kernel_svc', SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
# decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
# kernel='poly', max_iter=-1, probability=False, random_state=None,
# shrinking=True, tol=0.001, verbose=False))])
plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x1[y1==0, 0], x1[y1==0, 1])
plt.scatter(x1[y1==1, 0], x1[y1==1, 1])
plt.show()
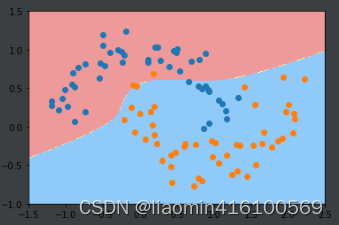
这种方法就是svm中kernel函数。接下来具体说明核函数。
什么是核函数
在现实任务中,原始的样本空间也许并不存在一个能正确划分两类的超平面,对于这样一个问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。因此核函数的作用就是使得原本线性不可分的数据变得线性可分。下面是一个使用多项式核映射的过程。

转换为以下函数后,数据变的线性可分。
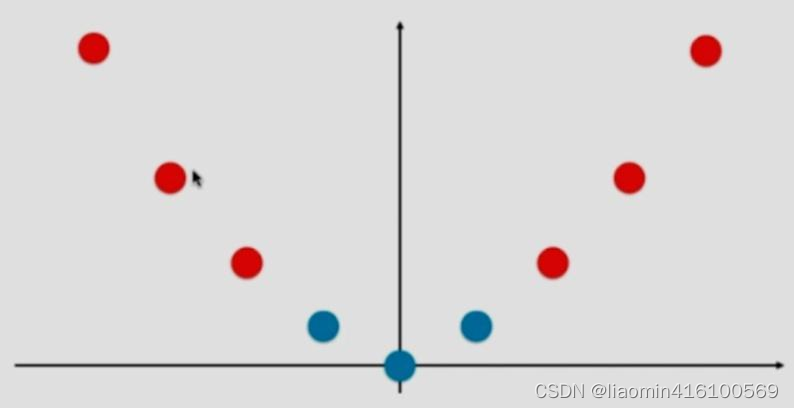
常用 核函数:
1、线性核:
k
(
x
i
,
x
j
)
=
x
i
T
x
j
+
c
k(x_{i}, x_{j}) = x_{i}^T x_{j} + c
k(xi,xj)=xiTxj+c
2、多项式核:
k
(
x
i
,
x
j
)
=
(
x
i
T
x
j
+
c
)
d
k(x_{i}, x_{j}) = (x_{i}^T x_{j} + c)^d
k(xi,xj)=(xiTxj+c)d,当d=1时退化为线性核。
3、高斯核RBF:
k
(
x
i
,
x
j
)
=
e
x
p
(
−
∥
x
i
−
x
j
∥
2
2
σ
2
)
,
σ
>
0
k(x_{i}, x_{j}) = exp(-\frac{\parallel x_{i} - x_{j} \parallel ^2}{2\sigma ^2}), \sigma >0
k(xi,xj)=exp(−2σ2∥xi−xj∥2),σ>0为高斯核的带宽RBF核:Radial Basis Function Kernel
4、拉普拉斯核:
k
(
x
i
,
x
j
)
=
e
x
p
(
−
∥
x
i
−
x
j
∥
σ
)
,
σ
>
0
k(x_{i}, x_{j}) = exp(-\frac{\parallel x_{i} - x_{j} \parallel}{\sigma}), \sigma > 0
k(xi,xj)=exp(−σ∥xi−xj∥),σ>0
5、Sigmoid核:
k
(
x
i
,
x
j
)
=
t
a
n
h
(
β
x
i
T
x
j
+
θ
)
k(x_{i}, x_{j}) = tanh(\beta x_{i}^T x_{j} + \theta)
k(xi,xj)=tanh(βxiTxj+θ)
高斯核函数
高斯核函数是一种常用的核函数,通常用于支持向量机(SVM)等机器学习算法中。它可以将数据从原始空间映射到更高维的空间,使得原本不可分的样本在新的空间中可以被分离开来。
通俗地说,高斯核函数就像是一种“相似度度量方式”,它可以计算出两个样本之间的相似度。在使用高斯核函数时,我们会首先选择一个中心点,然后计算每个样本点与中心点之间的距离,并将距离作为相似度的度量值。这个距离通常用高斯分布函数进行加权,这也是高斯核函数名称的由来。
更具体地说,高斯核函数可以将两个样本点
x
i
x_i
xi和
x
j
x_j
xj映射到更高维的空间中,计算它们在新空间中的内积,得到如下公式:
K
(
x
i
,
x
j
)
=
exp
(
−
γ
∣
∣
x
i
−
x
j
∣
∣
2
)
K(x_i, x_j) = \exp(-\gamma ||x_i - x_j||^2)
K(xi,xj)=exp(−γ∣∣xi−xj∣∣2)
其中, γ \gamma γ是一个控制高斯分布宽度的参数, ∣ ∣ x i − x j ∣ ∣ 2 ||x_i - x_j||^2 ∣∣xi−xj∣∣2是样本点 x i x_i xi和 x j x_j xj之间的欧几里得距离的平方。当 γ \gamma γ取值较大时,高斯分布的峰值会变得较窄,相似度的度量会更加关注两个样本点之间的距离;当 γ \gamma γ取值较小时,高斯分布的峰值会变得较宽,相似度的度量会更加平滑,关注两个样本点之间的整体相似度。
总的来说,高斯核函数是一种非常灵活、强大的相似度度量方式,可以用于许多机器学习算法中,特别是涉及到非线性分类问题时。


接下来通过高斯核函数映射来更加直观地理解整个映射的过程。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-4, 5, 1)
# array([-4, -3, -2, -1, 0, 1, 2, 3, 4])
y = np.array((x >= -2) & (x <= 2), dtype='int')
# array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.scatter(x[y==0], [0] * len(x[y==0]))
plt.scatter(x[y==1], [0] * len(x[y==1]))
plt.show()

高斯核后
def gaussian(x, l):
gamma = 1.0
return np.exp(-gamma *(x-l)**2)
l1, l2 = -1, 1
x_new = np.empty((len(x), 2))
for i,data in enumerate(x):
x_new[i, 0] = gaussian(data, l1)
x_new[i, 1] = gaussian(data, l2)
plt.scatter(x_new[y==0, 0], x_new[y==0, 1])
plt.scatter(x_new[y==1, 0], x_new[y==1, 1])
plt.show()

其实,真正的高斯核函数实现的过程中并不是固定的
γ
\gamma
γ,而是对于每一个数据点都是
γ
\gamma
γ,这里写死 gamma = 1.0。
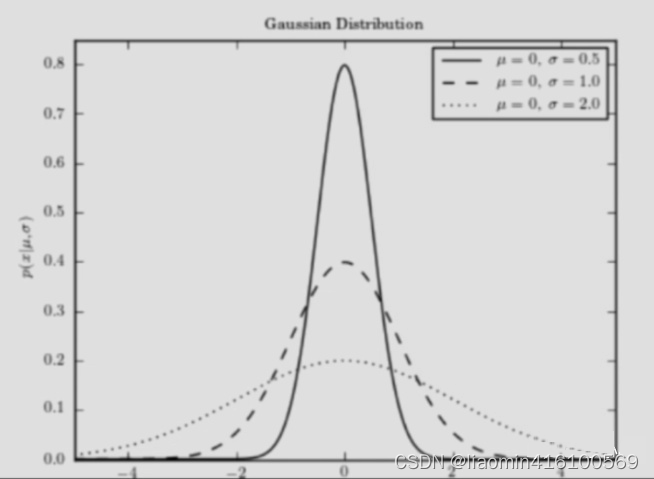
高斯函数:
g
(
x
)
=
1
σ
2
π
e
−
1
2
(
x
−
μ
σ
)
g(x)= \frac{1}{\sigma \sqrt{2 \pi} } e^{-\frac{1}{2}(\frac{x - \mu}{\sigma})}
g(x)=σ2π1e−21(σx−μ)
其中
μ
\mu
μ决定了函数的中心位置,
σ
\sigma
σ决定了整个图形 的靠拢程度,
σ
\sigma
σ越小,图像越高,图像相对比较集中。相反
σ
\sigma
σ越大,图形就越分散。
K
(
x
i
,
x
j
)
=
e
−
γ
∥
x
i
−
x
j
∥
2
K(x_{i},x_{j}) = e^{-\gamma \parallel x_{i} - x_{j} \parallel ^2}
K(xi,xj)=e−γ∥xi−xj∥2
γ
\gamma
γ越大,高斯分布越宽;
γ \gamma γ越小,高斯分布越窄。
接下来,使用sklearn中封装的高斯核函数:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x, y = datasets.make_moons(noise=0.15, random_state=666)
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scale', StandardScaler()),
('svc', SVC(kernel='rbf', gamma=gamma))
])
svc = RBFKernelSVC(gamma=1.0)
svc.fit(x, y)
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1),)
x_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(x_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()

svc_gamma100 = RBFKernelSVC(gamma=100)
svc_gamma100.fit(x, y)
plot_decision_boundary(svc_gamma100, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()

svc_gamma10 = RBFKernelSVC(gamma=10)
svc_gamma10.fit(x, y)
plot_decision_boundary(svc_gamma10, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()

svc_gamma01 = RBFKernelSVC(gamma=0.1)
svc_gamma01.fit(x, y)
plot_decision_boundary(svc_gamma01, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0, 0], x[y==0, 1])
plt.scatter(x[y==1, 0], x[y==1, 1])
plt.show()
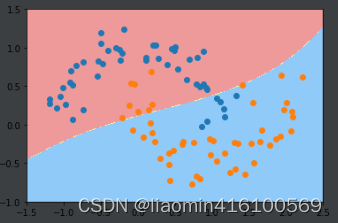
gamma相当于是在调节模型的复杂度,gammma越小模型复杂度越低,gamma越高模型复杂度越高。因此需要调节超参数gamma平衡过拟合和欠拟合。
本文文字和例题来源:
- https://cuijiahua.com/blog/2017/11/ml_8_svm_1.html
- https://zhuanlan.zhihu.com/p/79679104