名义模型干扰观测器

理论推导

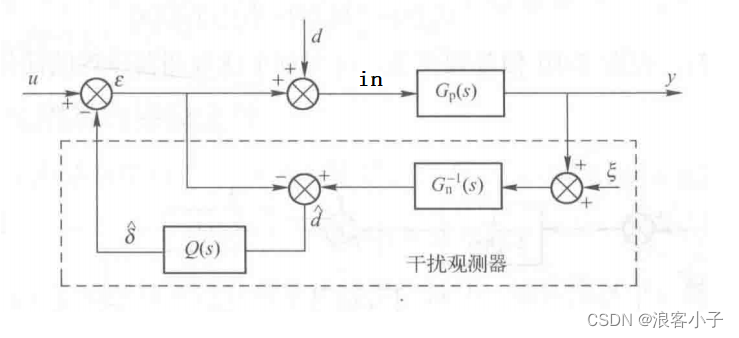
  所谓被控对象的名义模型，就是说，实际被控对象无论是通过系统建模还是系统辨识，都无法获得十分精确的参数，名义模型就是与实际系统模型相近的模型，可近似二者相同，即

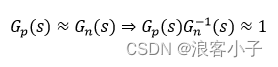
则

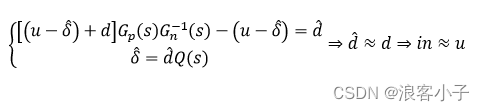
连续系统

令

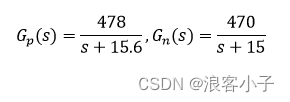
干扰信号为在$5-6s$内将输入信号幅值减小3个单位，如下所示：

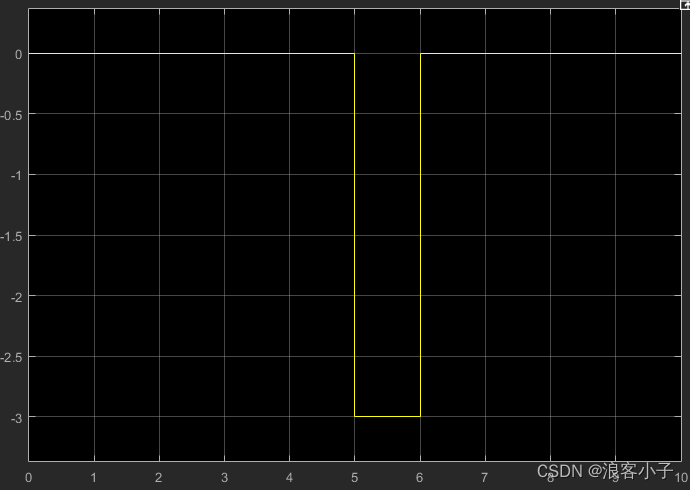
添加扰动补偿

系统框图如下：

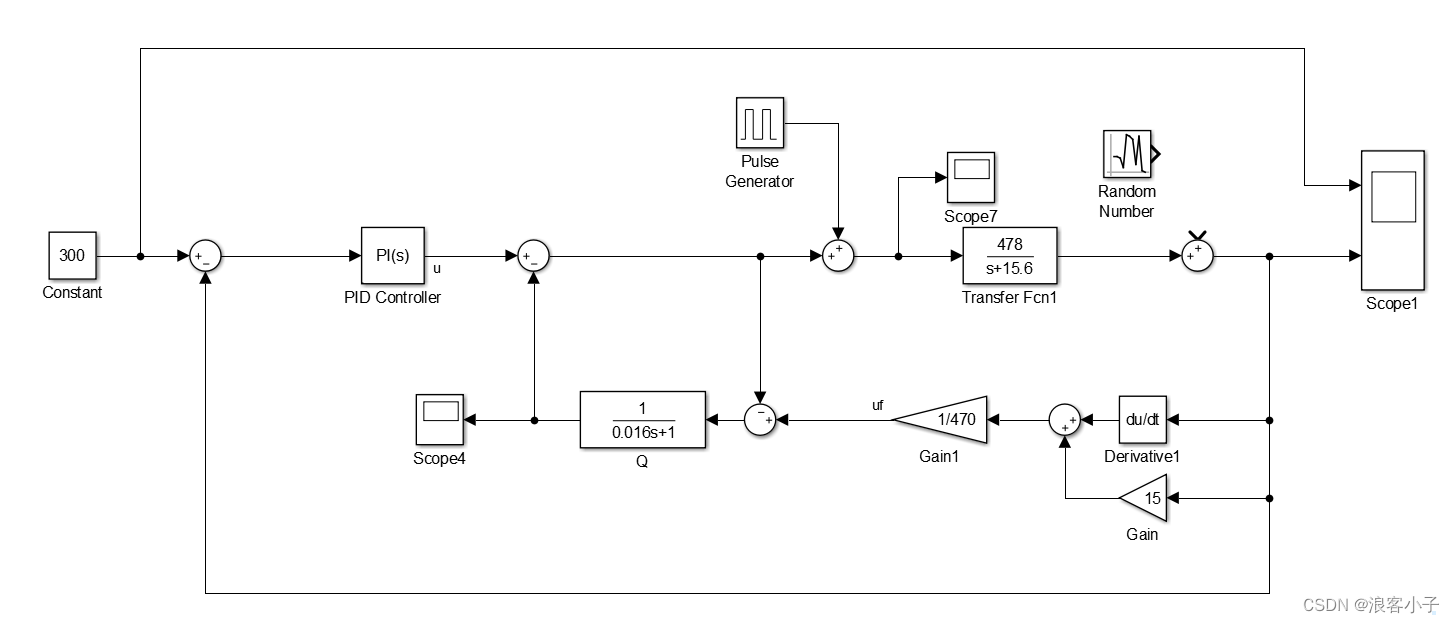
输出响应：

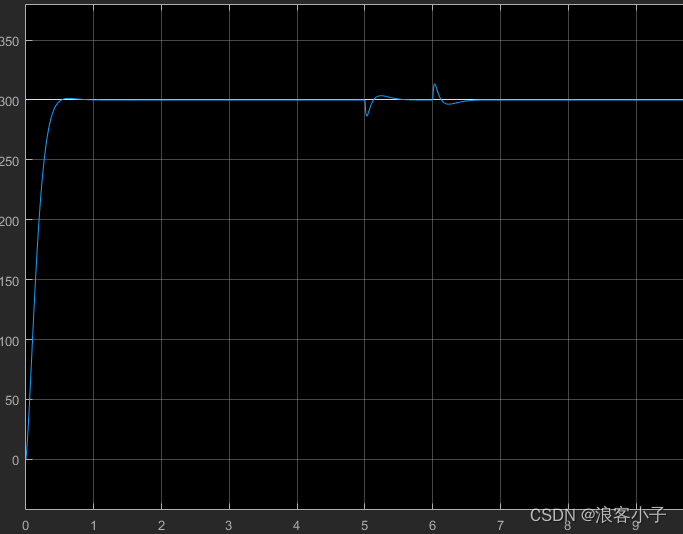
由上图可以看出，系统响应在$5-6s$内出现波动，但幅度不大。

系统实际输入信号$in$如下所示：

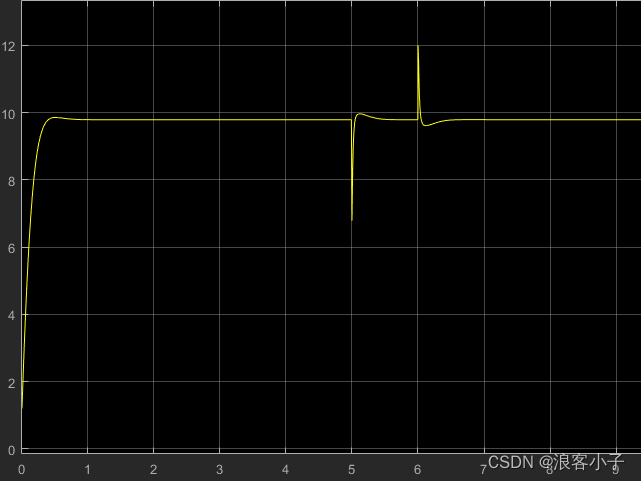
可见，信号$in$很快将干扰信号衰减掉。

不添加扰动补偿

系统框图如下：

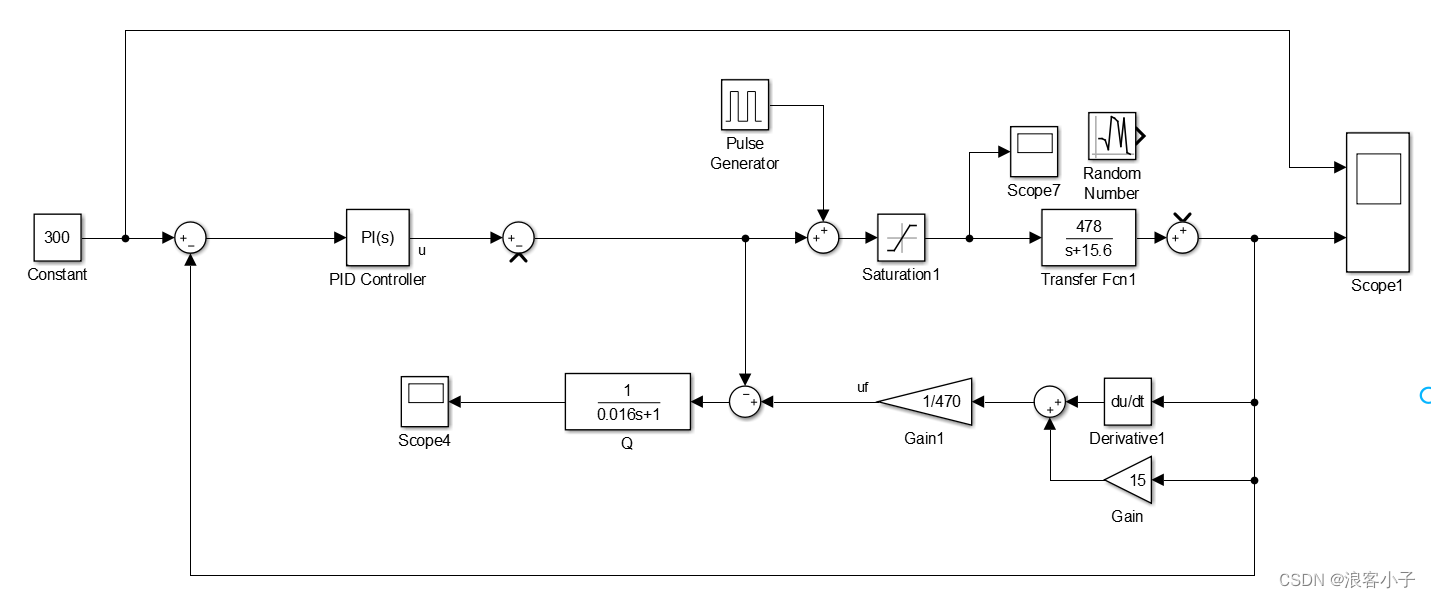
输出响应：

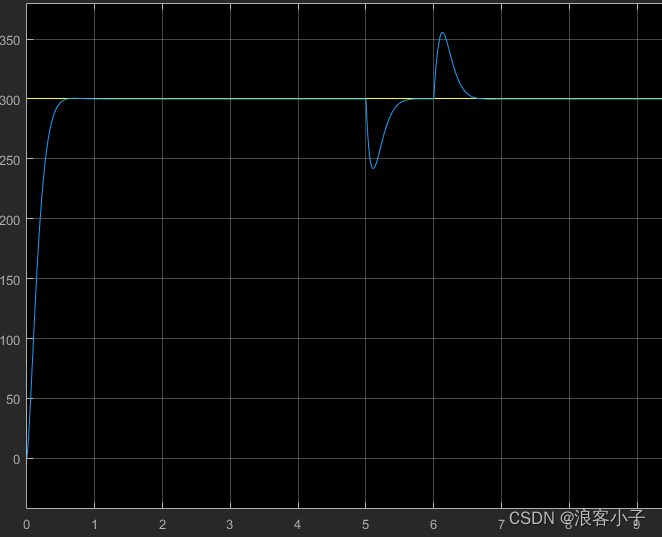
由上图可见，不添加扰动补偿时，系统输出响应在$5-6s$内波动幅度较大。

系统实际输入信号$in$如下所示：

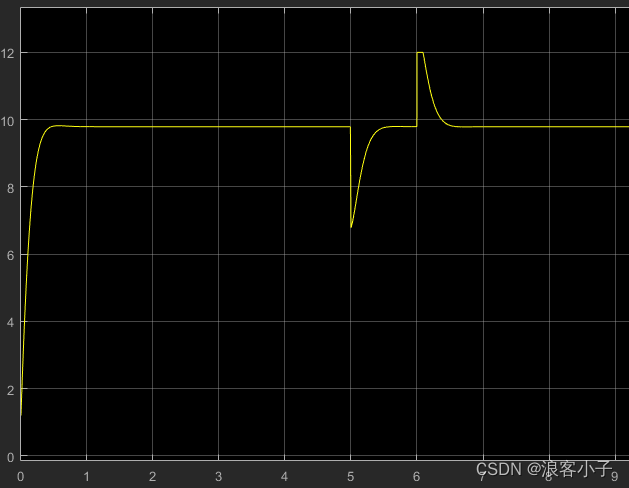
信号$in$对干扰信号衰的衰减速度就比较慢了。
  通过对比可见，加入扰动补偿后，系统的响应更加平稳，抗干扰能力明显增强，但也有明显的缺点，就是估计扰动信号时引入了微分，其将会放大噪声的影响，而低通滤波器$Q(s)$又不能将截止频率设置的很低，否则系统将会降低干扰信号的衰减速度，最终不能达到预期效果。添加测量噪声后，系统响应如下：

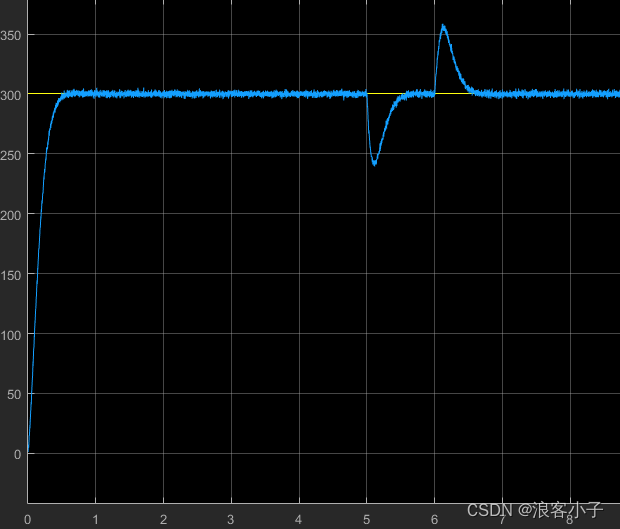
这就很糟糕了。

离散系统

系统框图如下：

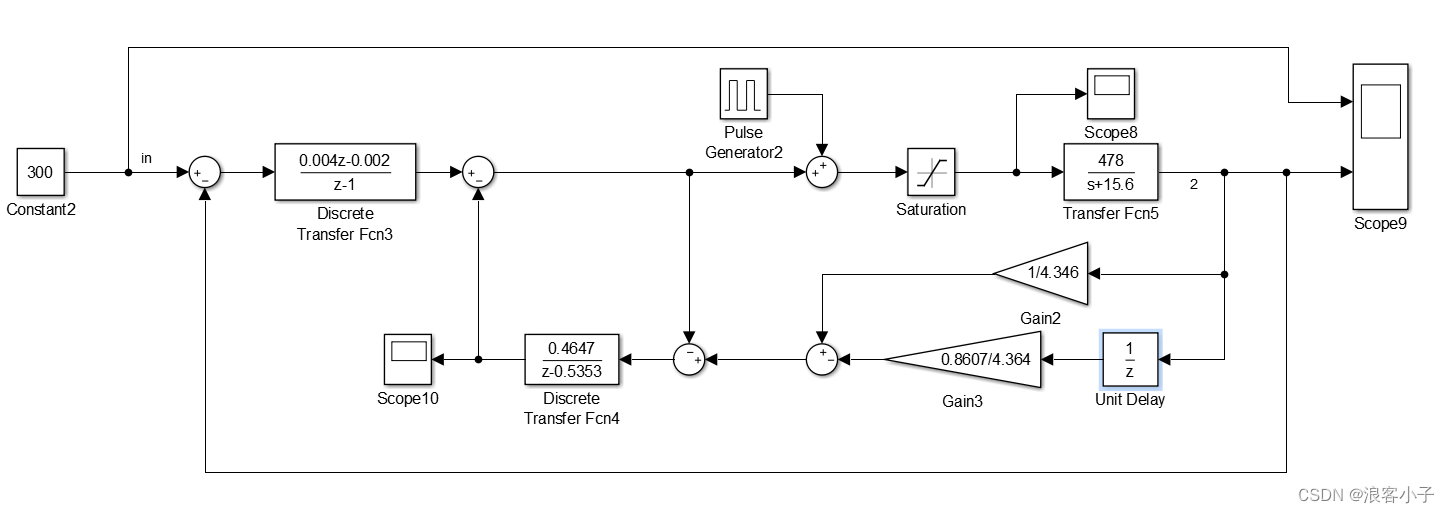
系统响应如下：

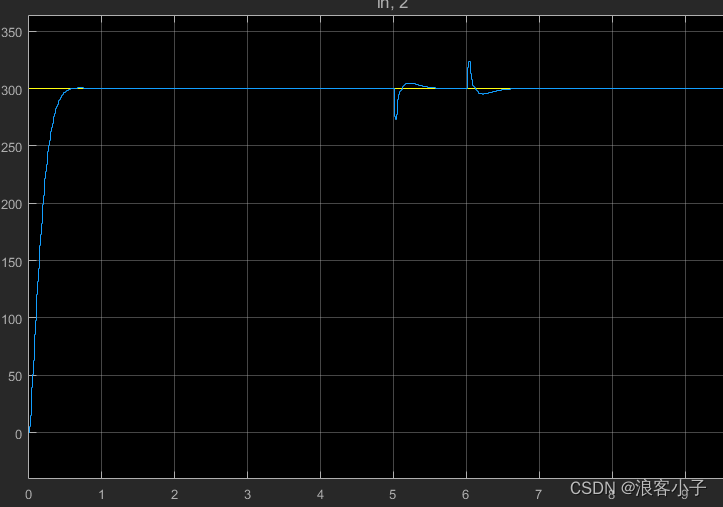
指数收敛干扰观测器

理论分析

假设某一阶系统如下：

可得

  设计观测器的思想就是，利用估计值与实际值的差值来修正估计值，可将观测器设计为

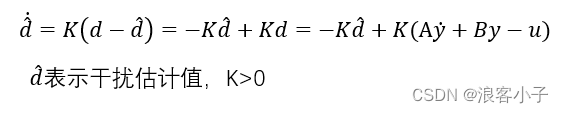
干扰$d$的变化是缓慢的，即

令观测误差为

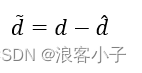
则

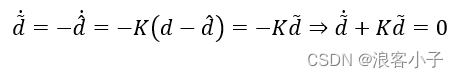
该微分方程的解为

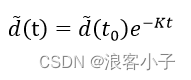
由上式可知，观测误差是呈指数收敛的，收敛速度由$K$决定。我们再看看设计的观测器

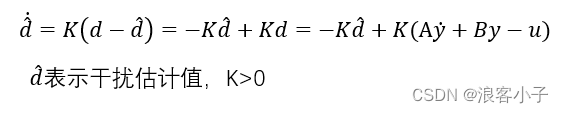
这个观测器并不是完美的，因为有系统输出的微分，这与名义模型干扰观测器有相同的不足，故而还需要对观测器进行改善。将上式变形

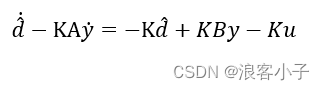
令

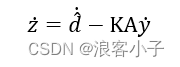
则

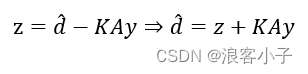
于是有

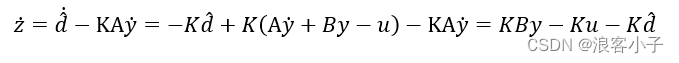
那么新的观测器设计为

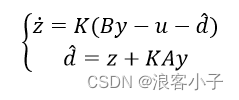
可以看出，新的观测器不在有系统输出的微分，利用辅助变量$z$相当于对模型降阶，再来对这个干扰观测器进行分析

该微分方程的解为

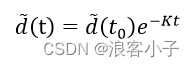
仿真

仍以上述系统为例：

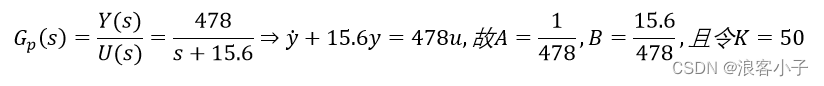
系统框图如下：

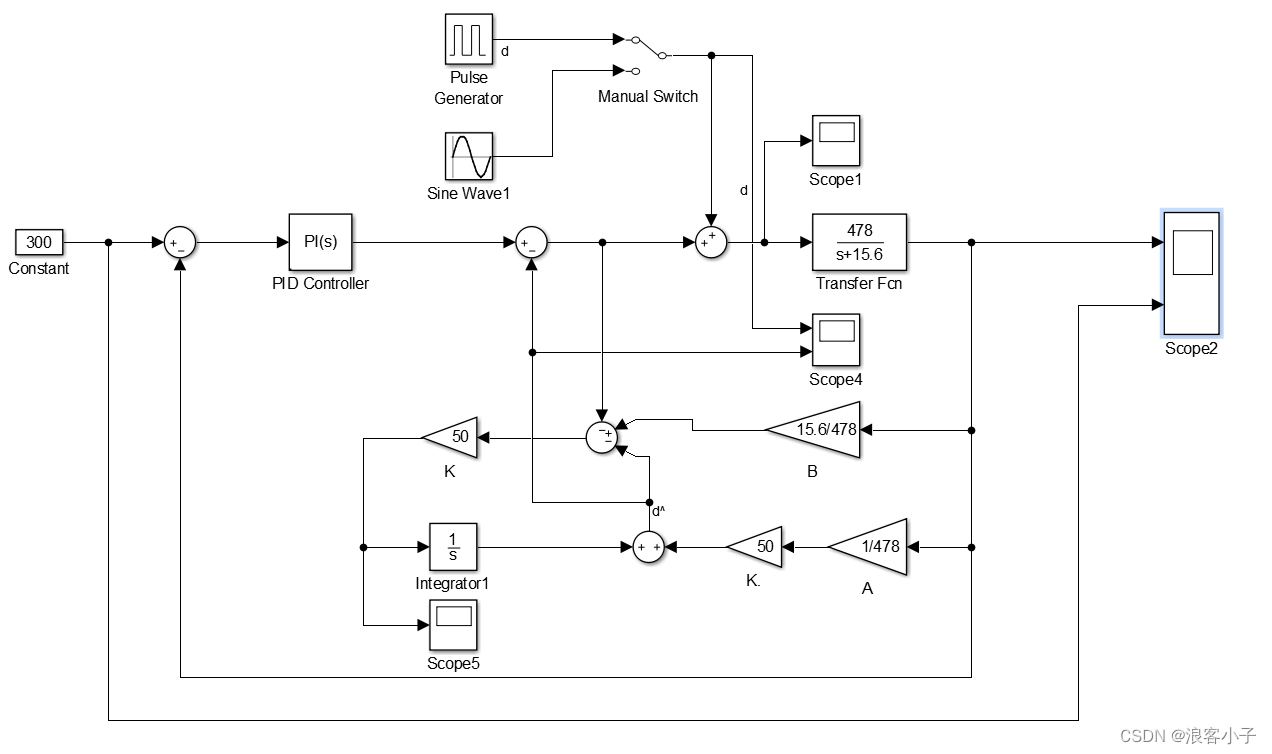
系统响应：

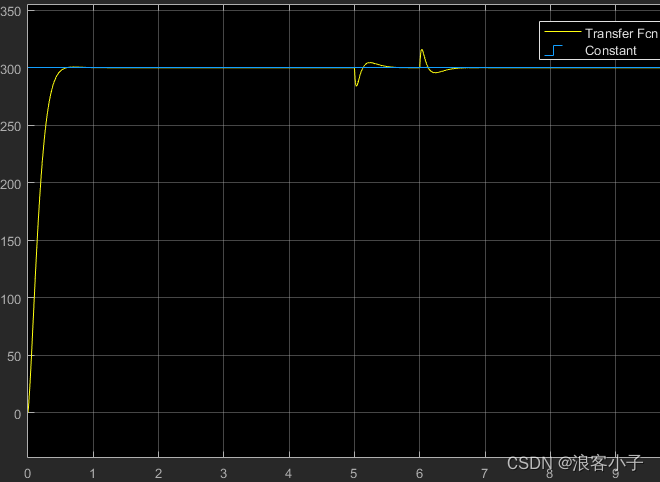
可见系统受干扰的影响较小，再看看估计的干扰值

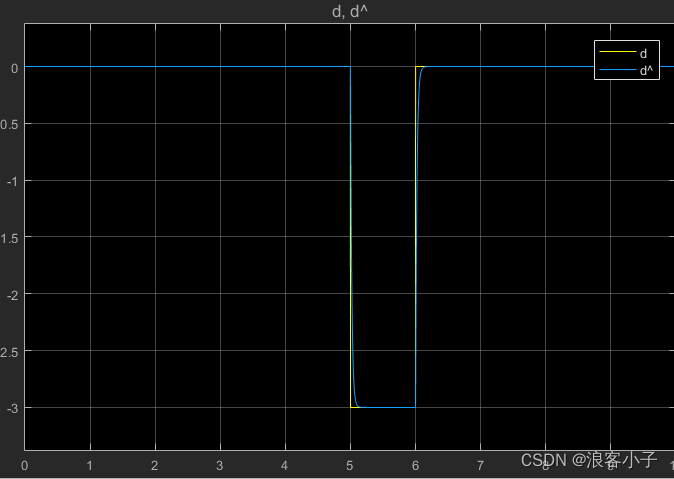
可见，对干扰的观测效果较好，我们在看看正弦干扰信号的观测

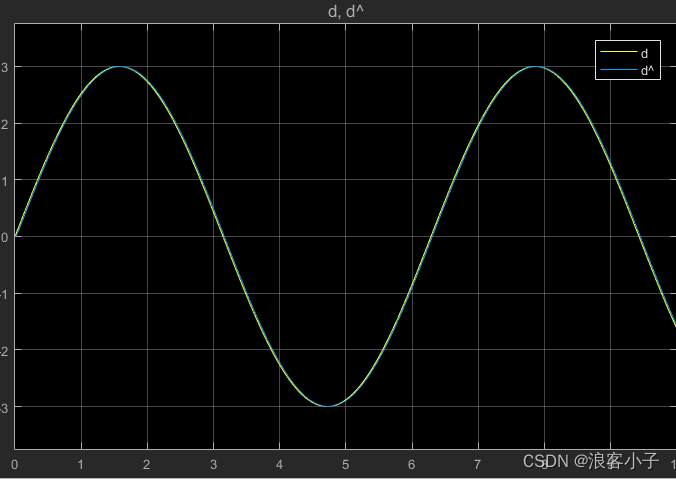
可见对正弦干扰信号的观测效果也较为理想。