目录
- 试题 A. 阶乘求和
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 B.幸运数字
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 C.数组分割
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 D.矩形总面积
- 1.问题描述
- 2.解题思路
- 3.模板代码
- 试题 E.蜗牛
- 1.问题描述
- 2.解题思路
- 3.模板代码
- 试题 F.合并区域
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 G.买二赠一
- 1.问题描述
- 2.解题思路
- 3.模板代码
- 试题 H.合并石子
- 1.问题描述
- 2.解题思路
- 3.模板代码
- 试题 I.最大开支
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 J. 魔法阵
- 1.题目描述
- 2.解题思路
- 3.模板代码
别问为什么不用 Java 写,Java简直依托答辩。
感觉 Java 组难度有点大
试题 A. 阶乘求和
1.题目描述
令
S
=
1
!
+
2
!
+
3
!
+
.
.
.
+
202320232023
!
S = 1! + 2! + 3! + ... + 202320232023!
S=1!+2!+3!+...+202320232023!,求
S
S
S 的末尾
9
9
9 位数字。
提示:答案首位不为
0
0
0。
2.解题思路
阶乘增加很快,
45
!
45!
45! 的末九位数就全都为
0
0
0 了(当然是Pythond打表看的),因为我们只需要末九位数字,所以后面的数都不会增加贡献,枚举前
45
45
45 位数即可。答案为420940313。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s)
#define sz(s) ((int)s.size())
#define x first
#define y second
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000000;
const int N = 200010;
void solve()
{
LL x = 1;
LL ans = 0;
for (int i = 1; i <= 45; ++i) {
x *= i;
x %= mod;
ans = (ans + x) % mod;
}
cout << ans << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
while (t--)
{
solve();
}
return 0;
}
试题 B.幸运数字
1.题目描述
哈沙德数是指在某个固定的进位制当中,可以被各位数字之和整除的正整数。例如
126
126
126 是十进制下的一个哈沙德数,因为
(
126
)
10
m
o
d
(
1
+
2
+
6
)
=
0
(126)_{10} \mod (1+2+6) = 0
(126)10mod(1+2+6)=0;
126
126
126 也是八进制下的哈沙德数,因为
(
126
)
10
=
(
176
)
8
,
(
126
)
10
m
o
d
(
1
+
7
+
6
)
=
0
;
(126)_{10} = (176)_8,(126)_{10} \mod (1 + 7 + 6) = 0;
(126)10=(176)8,(126)10mod(1+7+6)=0;同时
126
126
126 也是
16
16
16 进制下的哈沙德数,因为
(
126
)
10
=
(
7
e
)
16
,
(
126
)
10
m
o
d
(
7
+
e
)
=
0
。
(126)_{10} = (7e)_{16},(126)_{10} \mod (7+e) = 0。
(126)10=(7e)16,(126)10mod(7+e)=0。 小蓝认为,如果一个整数在二进制、八进制、十进制、十六进制下均为哈沙德数,那么这个数字就是幸运数字,第
1
1
1 至第
10
10
10 个幸运数字的十进制表示
为:
1
,
2
,
4
,
6
,
8
,
40
,
48
,
72
,
120
,
126...
。
1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。
1,2,4,6,8,40,48,72,120,126...。现在他想知道第
2023
2023
2023 个幸运数字是多少?你只需要告诉小蓝这个整数的十进制表示即可。
2.解题思路
模拟一下。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s)
#define sz(s) ((int)s.size())
#define x first
#define y second
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;
bool check(int x, int v) {
int g = x;
int m = 0;
while (x) {
m += x % v;
x /= v;
}
return g % m == 0;
}
void solve()
{
int ans = 0;
int l = 1;
while (1) {
if (check(l, 2) && check(l, 8) && check(l, 10) && check(l, 16)) {
ans++;
}
if (ans == 2023) {
cout << l << '\n';
break;
}
l++;
}
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
while (t--)
{
solve();
}
return 0;
}
试题 C.数组分割
1.题目描述
小蓝有一个长度为 N N N 的数组 A = [ A 0 , A 1 , . . . , A N − 1 ] A = [A_0, A_1, . . . , A_{N−1}] A=[A0,A1,...,AN−1]。现在小蓝想要从 A A A 对应的数组下标所构成的集合 I = { 0 , 1 , 2 , . . . , N − 1 } I = \{ 0, 1, 2, . . . , N − 1\} I={0,1,2,...,N−1} 中找出一个子集 R 1 R_1 R1,那么 R 1 R_1 R1在 I I I 中的补集为 R 2 R_2 R2。记 S 1 = ∑ r ∈ R 1 A r , S 2 = ∑ r ∈ R 2 A r S_1 =∑_{r∈R1}A_r,S_2 =∑_{r∈R_2}Ar S1=∑r∈R1Ar,S2=∑r∈R2Ar,我们要求 S 1 S_1 S1 和 S 2 S_2 S2 均为偶数,请问在这种情况下共有多少种不同的 R 1 R_1 R1。当 R 1 R_1 R1 或 R 2 R_2 R2 为空集时我们将 S 1 S_1 S1 或 S 2 S_2 S2 视为 0 0 0。
2.解题思路
咋感觉大家都用组合数分类讨论,这里用了个简单的动规做法(不会是个假做法吧)。题意无非就是让你将数分为两堆,每堆的和都是偶数,那么显然总和为奇数时即为无解。
当一堆为偶数时,另一堆一定也为偶数,问题转化为从
n
n
n 个数中选出若干个数的和为偶数有多少种方案。
定义
f
[
i
]
[
0
]
f[i][0]
f[i][0] 为只考虑前
i
i
i 个数且总和为偶数的方案数,
f
[
i
]
[
1
]
f[i][1]
f[i][1] 为只考虑前
i
i
i 个数且综合为奇数的方案数。题目允许不选元素,所以初始化
f
[
0
]
[
0
]
=
1
f[0][0]=1
f[0][0]=1,最终答案即为
f
[
n
]
[
0
]
f[n][0]
f[n][0]。
状态转移也很简单,当第
i
i
i 个数为奇数时,选上它奇数序列会变偶数,偶数序列变奇数。当第
i
i
i 个数为偶数时,偶数序列仍然为偶数序列,奇数序列仍然为奇数序列。
f
[
i
]
[
0
]
=
{
f
[
i
−
1
]
[
0
]
+
f
[
i
−
1
]
[
1
]
a[i]为奇数
f
[
i
−
1
]
[
0
]
×
2
a[i]为偶数
f[i][0] = \begin{cases} f[i-1][0]+f[i-1][1] &\text{a[i]为奇数}\\ f[i-1][0] \times 2 &\text{a[i]为偶数}\\ \end{cases}
f[i][0]={f[i−1][0]+f[i−1][1]f[i−1][0]×2a[i]为奇数a[i]为偶数
f
[
i
]
[
1
]
=
{
f
[
i
−
1
]
[
0
]
+
f
[
i
−
1
]
[
1
]
a[i]为奇数
f
[
i
−
1
]
[
1
]
×
2
a[i]为偶数
f[i][1] = \begin{cases} f[i-1][0]+f[i-1][1] &\text{a[i]为奇数}\\ f[i-1][1] \times 2 &\text{a[i]为偶数}\\ \end{cases}
f[i][1]={f[i−1][0]+f[i−1][1]f[i−1][1]×2a[i]为奇数a[i]为偶数
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;
int n;
int a[N], f[N][2];
void solve()
{
cin >> n;
LL ans = 0;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
ans += a[i];
}
if (ans % 2) {
cout << 0 << '\n';
return;
}
f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
if (a[i] % 2) {
f[i][0] = (f[i - 1][0] + f[i - 1][1]) % mod;
f[i][1] = (f[i - 1][1] + f[i - 1][0]) % mod;
} else {
f[i][0] = (f[i - 1][0] * 2) % mod;
f[i][1] = (f[i - 1][1] * 2) % mod;
}
}
cout << f[n][0] << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
试题 D.矩形总面积
1.问题描述
平面上有个两个矩形
R
1
R1
R1 和
R
2
R2
R2,它们各边都与坐标轴平行。设
(
x
1
,
y
1
)
(x1, y1)
(x1,y1) 和
(
x
2
,
y
2
)
(x2, y2)
(x2,y2) 依次是
R
1
R1
R1 的左下角和右上角坐标,
(
x
3
,
y
3
)
(x3, y3)
(x3,y3) 和
(
x
4
,
y
4
)
(x4, y4)
(x4,y4) 依次是
R
2
R2
R2 的左下角和右上角坐标,请你计算
R
1
R1
R1 和
R
2
R2
R2 的总面积是多少?
注意:如果
R
1
R1
R1 和
R
2
R2
R2 有重叠区域,重叠区域的面积只计算一次。
2.解题思路
正确做法就是容斥,两个矩阵的面积和减去重叠的面积。重叠面积的求法就是求出两个矩阵在
x
x
x 轴和
y
y
y 轴的交集。怎么tm是原中原题。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s)
#define sz(s) ((int)s.size())
#define x first
#define y second
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;
LL a[8];
void solve()
{ //01 23 45 67
for (int i = 0; i <= 7; ++i) cin >> a[i];
LL x = max(0LL, min(a[2], a[6]) - max(a[0], a[4]));
LL y = max(0LL, min(a[3], a[7]) - max(a[1], a[5]));
LL res = (a[2] - a[0]) * (a[3] - a[1]) + (a[6] - a[4]) * (a[7] - a[5]) - x * y;
cout << res << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
while (t--)
{
solve();
}
return 0;
}
试题 E.蜗牛
1.问题描述
这天,一只蜗牛来到了二维坐标系的原点。在 x x x 轴上长有 n n n 根竹竿。它们平行于 y y y 轴,底部纵坐标为 0 0 0,横坐标分别为 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn。竹竿的高度均为无限高,宽度可忽略。蜗牛想要从原点走到第 n n n 个竹竿的底部也就是坐标 ( x n , 0 ) (x_n, 0) (xn,0)。它只能在 x x x 轴上或者竹竿上爬行,在 x x x 轴上爬行速度为 1 1 1 单位每秒;由于受到引力影响,蜗牛在竹竿上向上和向下爬行的速度分别为 0.7 0.7 0.7 单位每秒和 1.3 1.3 1.3 单位每秒。为了快速到达目的地,它施展了魔法,在第 i i i 和 i + 1 i + 1 i+1 根竹竿之间建立了传送门 ( 0 < i < n ) (0 < i < n) (0<i<n),如果蜗牛位于第 i i i 根竹竿的高度为 a i ai ai 的位置 ( x i , a i ) (x_i, a_i) (xi,ai),就可以瞬间到达第 i + 1 i + 1 i+1 根竹竿的高度为 b i + 1 b_i+1 bi+1 的位置 ( x i + 1 , b i + 1 ) (x_i+1, b_i+1) (xi+1,bi+1),请计算蜗牛最少需要多少秒才能到达目的地。
2.解题思路
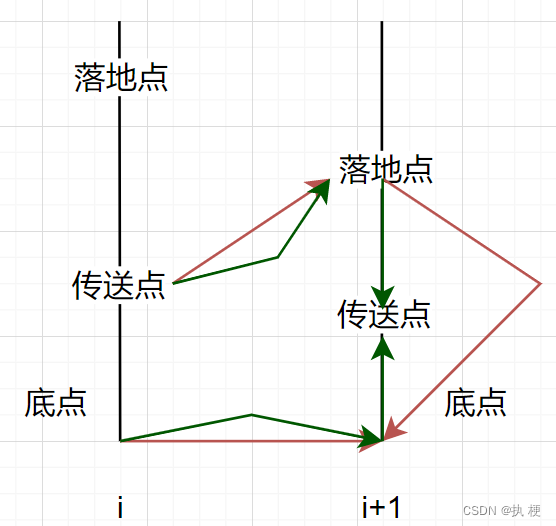
显然一根杆我们需要关注它到达转送点的最短时间和底点的最短时间,注意的传送点是从这根杆到下一根杆的传送点,而不是上根杆传送到当前杆的落地点。
定义
f
[
i
]
[
0
]
f[i][0]
f[i][0] 表示到达第
i
i
i 根杆底点的最小时间,
f
[
i
]
[
1
]
f[i][1]
f[i][1] 表示到达第
i
i
i 根杆传送点的最短时间。底点可以考虑从上一个底点或者上一个传送点转移,传送点也可以考虑从上一个底点或者传送点转移,这里需要注意的是落地点有可能在传送点上,也可能在传送点下,需要分类讨论。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s)
#define sz(s) ((int)s.size())
#define x first
#define y second
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 100010;
int n;
double x[N], a[N], b[N];
double f[N][2];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i) cin >> x[i];
for (int i = 1; i < n; ++i) cin >> a[i] >> b[i + 1];
//地上
f[1][0] = x[1];
//杆上的传送点
f[1][1] = x[1] + (a[1] / 0.7);
for (int i = 2; i <= n; ++i) {
//考虑传送点的转移
f[i][1] = f[i - 1][0] + x[i] - x[i - 1] + (a[i] / 0.7);
if (b[i] >= a[i]) f[i][1] = min(f[i][1], f[i - 1][1] + (b[i] - a[i]) / 1.3);
else f[i][1] = min(f[i][1], f[i - 1][1] + (a[i] - b[i]) / 0.7);
//考虑地上的转移
f[i][0] = min(f[i - 1][0] + x[i] - x[i - 1], f[i - 1][1] + (b[i] / 1.3));
}
cout << f[n][0] << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << setiosflags(ios::fixed) << setprecision(2);
int t = 1;
while (t--)
{
solve();
}
return 0;
}
试题 F.合并区域
1.题目描述
小蓝在玩一款种地游戏。现在他被分配给了两块大小均为
N
×
N
N × N
N×N 的正方形区域。这两块区域都按照
N
×
N
N × N
N×N 的规格进行了均等划分,划分成了若干块面积相同的小区域,其中每块小区域要么是岩石,要么就是土壤,在垂直或者水平方向上相邻的土壤可以组成一块土地。现在小蓝想要对这两块区域沿着边缘进行合并,他想知道合并以后可以得到的最大的一块土地的面积是多少(土地的面积就是土地中土壤小区域的块数)?
在进行合并时,小区域之间必须对齐。可以在两块方形区域的任何一条边上进行合并,可以对两块方形区域进行 90 度、180 度、270 度、360 度的旋转,但不可以进行上下或左右翻转,并且两块方形区域不可以发生重叠。
2.解题思路
看着像分类讨论的大模拟,暂更。
3.模板代码
试题 G.买二赠一
1.问题描述
某商场有 N N N 件商品,其中第 i i i 件的价格是 A i Ai Ai。现在该商场正在进行 “买二赠一” 的优惠活动,具体规则是:每购买 2 2 2 件商品,假设其中较便宜的价格是 P P P(如果两件商品价格一样,则 P P P 等于其中一件商品的价格),就可以从剩余商品中任选一件价格不超过 P 2 \frac P2 2P的商品,免费获得这一件商品。可以通过反复购买 2 2 2 件商品来获得多件免费商品,但是每件商品只能被购买或免费获得一次。小明想知道如果要拿下所有商品(包含购买和免费获得),至少要花费多少钱?
2.解题思路
直观的思路肯定是每次买最大和次大,这样得到的免费购买额度才会尽量大。但如何使用免费机会是关键,我看很多人做法都是去二分标记删除。但其实完全没必要,我们并不需要立刻使用这个免费的机会,我们可以将其存入队列中。
每次考虑当前最贵的物品,如果队头的免费机会可以买当前物品我们则使用这个机会,否则用钱购买,当用钱购买了两件商品,则向队尾加入第二件商品价格的一半视为一次免费机会,显然这样贪心的做法很正确。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 500010;
int n;
int a[N];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
sort(a + 1, a + n + 1);
queue<int> q;
int p = n;
LL ans = 0;
while (p >= 1) {
while (q.size() && p >= 1 && q.front() >= a[p]) {
q.pop();
p--;
}
//先买第一个
ans += a[p];
p--;
while (q.size() && p >= 1 && q.front() >= a[p]) {
q.pop();
p--;
}
//再买第二个
ans += a[p];
q.push(a[p] / 2);
p--;
}
cout << ans << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
while (t--)
{
solve();
}
return 0;
}
试题 H.合并石子
1.问题描述
在桌面从左至右横向摆放着
N
N
N 堆石子。每一堆石子都有着相同的颜色,颜色可能是颜色
0
0
0,颜色
1
1
1 或者颜色
2
2
2 中的其中一种。
现在要对石子进行合并,规定每次只能选择位置相邻并且颜色相同的堆石子进行合并。合并后新堆的相对位置保持不变,新堆的石子数目为所选择的两堆石子数目之和,并且新堆石子的颜色也会发生循环式的变化。具体来说:两堆颜色
0
0
0 的石子合并后的石子堆为颜色
1
1
1,两堆颜色
1
1
1 的石子合并后的石子堆为颜色
2
2
2,两堆颜色
2
2
2 的石子合并后的石子堆为颜色
0
0
0。本次合并花费为所选择的两堆石子的数目之和。给出
N
N
N 堆石子以及他们的初始颜色,请问最少可以将它们合并为多少堆石子?如果有多种答案,选择其中合并总花费最小的一种,合并总花费指的是在所有的合并操作中产生的合并花费的总和。
2.解题思路
代码写炸了,出题人怎么知道我不会区间dp,还好我是C++组的。有心情了再调,就是区间dp裸题的变种,话说隔壁 Python 组还出了个树形 dp 模板题的变种。
3.模板代码
暂更
试题 I.最大开支
1.题目描述
小蓝所在学校周边新开业了一家游乐园,小蓝作为班长,打算组织大家去游乐园玩。已知一共有
N
N
N 个人参加这次活动,游乐园有
M
M
M 个娱乐项目,每个项目都需要买门票后才可进去游玩。门票的价格并不是固定的,团购的人越多单价越便宜,当团购的人数大于某个阈值时,这些团购的人便可以免费进入项目进行游玩。这
M
M
M 个娱乐项目是独立的,所以只有选择了同一个项目的人才可以参与这个项目的团购。第 i 个项目的门票价格
H
i
Hi
Hi 与团购的人数
X
X
X 的关系可以看作是一个函数:
H
i
(
X
)
=
m
a
x
(
K
i
×
X
+
B
i
,
0
)
Hi(X) = max (Ki × X + Bi, 0)
Hi(X)=max(Ki×X+Bi,0)
max 表示取二者之中的最大值。当
H
i
=
0
Hi = 0
Hi=0 时说明团购人数达到了此项目的免单阈值。这
N
N
N 个人可以根据自己的喜好选择
M
M
M 个娱乐项目中的一种,或者有些人对这些娱乐项目都没有兴趣,也可以选择不去任何一个项目。每个人最多只会选择一个娱乐项目,如果多个人选择了同一个娱乐项目,那么他们都将享受对应的团购价格。小蓝想知道他至少需要准备多少钱,使得无论大家如何选择,他都有能力支付得起所有
N
N
N 个人购买娱乐项目的门票钱。
2.解题思路
题意变换过来,就是问你最贵的情况下门票要多少钱,感觉
O
(
n
2
)
O(n^2)
O(n2) 的
d
p
dp
dp 的话很好写,但这复杂度不行,那就只能硬贪了。每次在已经安排了
x
x
x 个人的基础上考虑第
x
+
1
x+1
x+1 个人,看这
m
m
m 个项目哪个项目再加一个人能产生的价值更高就把他安排去哪,这个寻找最大价值项目我们可以用优先队列维护起来,每个人都选择当前最优得到答案最优,复杂度
O
(
n
log
n
)
O(n \log n)
O(nlogn)。贪心不需要证明的。
需要注意一点的是如果当前最优的项目带来的价值都是负的,我们就不需要再考虑了,因为题意说了可以一个项目都不去。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
#define pb(s) push_back(s)
#define sz(s) ((int)s.size())
#define x first
#define y second
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;
int n, m;
struct node {
// c 表示当前项目已经放了几个人
LL k, v, c;
bool operator<(const node &a) const
{
LL x = (a.c + 1) * max(a.k * (a.c + 1) + a.v, 0LL) - a.c * max(a.k * a.c + a.v, 0LL);
LL y = (c + 1) * max(k * (c + 1) + v, 0LL) - c * max(k * c + v, 0LL);
return x > y;
}
};
void solve()
{
cin >> n >> m;
priority_queue<node> q;
for (int i = 1; i <= m; ++i) {
int k, v;
cin >> k >> v;
q.push({k, v, 0});
}
for (int i = 0; i < n; ++i) {
auto a = q.top(); q.pop();
if ((a.c + 1) * max(a.k * (a.c + 1) + a.v, 0LL) - a.c * max(a.k * a.c + a.v, 0LL) <= 0) {
q.push({a.k, a.v, a.c});
break;
}
q.push({a.k, a.v, a.c + 1});
}
LL ans = 0;
while (q.size()) {
auto g = q.top(); q.pop();
ans += g.c * max(g.k * g.c + g.v, 0LL);
}
cout << ans << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
while (t--)
{
solve();
}
return 0;
}
试题 J. 魔法阵
1.题目描述
魔法师小蓝为了营救自己的朋友小 Q Q Q,来到了敌人布置的魔法阵。魔法阵可以看作是一幅具有 N N N 个结点 M M M 条边的无向图,结点编号为 0 , 1 , 2 , . . . , N − 1 0, 1, 2, . . . , N − 1 0,1,2,...,N−1,图中没有重边和自环。敌人在每条边上都布置了陷阱,每条边都有一个伤害属性 w w w,每当小蓝经过一条边时就会受到这条边对应的 w w w 的伤害。小蓝从结点 0 0 0 出发,沿着边行走,想要到达结点 N − 1 N − 1 N−1 营救小 Q Q Q。小蓝有一种特殊的魔法可以使用,假设一条路径按照顺序依次经过了以下 L L L 条边: e 1 , e 2 , . . . , e L e_1, e_2, . . . , e_L e1,e2,...,eL(可以出现重复的边),那么期间小蓝受到的总伤害就是 P = ∑ i − 1 L = w ( e i ) P =\sum_{i-1}^{L}= w(e_i) P=∑i−1L=w(ei), w ( e i ) w(e_i) w(ei) 表示边 e i ei ei 的伤害属性。如果 L ≥ K L ≥ K L≥K,那么小蓝就可以从这 L 条边当中选出连续出现的 K 条边 e c , e c + 1 , . . . , e c + K − 1 e_c, e_{c+1}, . . . , e_{c+K−1} ec,ec+1,...,ec+K−1 并免去在这 K 条边行走期间所受到的伤害,即使用魔法之后路径总伤害变为 P ′ = P − ∑ i = c c + K − 1 = w ( e i ) P′ = P −\sum_{i=c}^{c+K−1}=w(e_i) P′=P−∑i=cc+K−1=w(ei)。注意必须恰好选出连续出现的 K K K 条边,所以当 L < K L < K L<K 时无法使用魔法。小蓝最多只可以使用一次上述的魔法,请问从结点 0 0 0 出发到结点 N − 1 N − 1 N−1 受到的最小伤害是多少?题目保证至少存在一条从结点 0 0 0 到 N − 1 N − 1 N−1 的路径。
2.解题思路
题目的意思大概意思就是从
0
0
0 到
n
−
1
n-1
n−1 的路径上你可以选择连续的
k
k
k 条边让它们的伤害不算入答案,问你到达终点受到的最小伤害是多少。
从我加深的题意来看,我们是可以选择兜圈,使得走的边数达到
k
k
k 条从而使用魔法让答案更优,所以贪心并不好写。考虑使用
d
p
dp
dp 解决问题,定义
f
[
i
]
[
j
]
f[i][j]
f[i][j] 为从点
0
0
0 走到点
i
i
i 且在这之前已经使用魔法砍掉了
j
j
j 条边受到的最小伤害。在这我定义在使用魔法的的边上的点为魔法点。
如下图当我们砍掉
1
−
2
1-2
1−2,
2
−
3
2-3
2−3,
3
−
4
3-4
3−4这三条边时,
1
,
2
,
3
,
4
1,2,3,4
1,2,3,4称为魔法点。
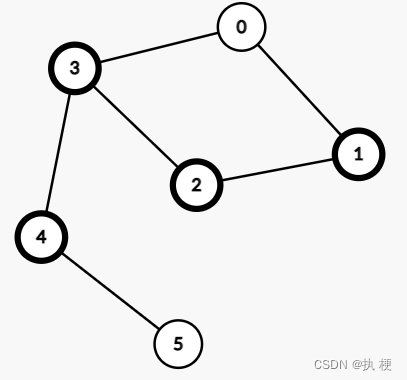
类似
d
i
j
k
s
t
r
a
dijkstra
dijkstra 一样,我们用起点不断去迭代到每个点的最短举例。我们假设有从点
u
−
>
v
u->v
u−>v 权值为
w
w
w 的一条边,分以下三种情况讨论:
- 当 j j j 等于 0 0 0 时,此时就是没有使用魔法的情况,那我们就正常迭代即可,判断一下 f [ v ] [ 0 ] > f [ u ] + w f[v][0]>f[u]+w f[v][0]>f[u]+w。
- 当 1 ≤ j ≤ k 1 \leq j \leq k 1≤j≤k时,此时应该判断 f [ v ] [ j ] > f [ u ] [ j − 1 ] f[v][j]>f[u][j-1] f[v][j]>f[u][j−1],因为题目说了砍边时必须是连续的 k k k 条边,不能前面砍一些后面砍一些,所以此时点 u u u 和点 v v v 一定是一个魔法点,从魔法点走到魔法点的边是不需要记录答案的。
- 当 j = k j=k j=k 时其实是比较特殊的,此时点 v v v 不一定是魔法点,因为在到达它之前可能我们早就已经砍掉了 k k k 条边。所以这里也需要判断 f [ v ] [ k ] > f [ u ] [ k ] + w f[v][k]>f[u][k]+w f[v][k]>f[u][k]+w。
根据上面这三种情况,我们不断更新每个点的最短距离,当然这里考虑的情况比较多,当某个点的任意一个
j
j
j 的值被更新,我们都应该将其重新加入队列,让它去迭代其他点,可以用数组标记以下某个点是否已经在队列中,减少无效入队次数。每个点反复入队次数不会超过
k
k
k 次。时间复杂度:
O
(
n
k
2
)
O(nk^2)
O(nk2)。
最后答案在
f
[
n
−
1
]
[
0
]
f[n-1][0]
f[n−1][0] 和
f
[
n
−
1
]
[
k
]
f[n-1][k]
f[n−1][k] 取个较小值,因为可能有路径不用魔法更优。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s)
#define sz(s) ((int)s.size())
#define x first
#define y second
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 1010;
const int M = 15;
int n, m, k;
//到点i且已经去掉了k条边受到的最小伤害
LL f[N][M];
std::vector<PII> e[N];
void solve()
{
cin >> n >> k >> m;
for (int i = 0; i < m; ++i) {
int u, v, w;
cin >> u >> v >> w;
e[u].push_back({v, w});
e[v].push_back({u, w});
}
ms(f, inf);
f[0][0] = 0;
queue<int> q;
q.push(0);
std::vector<int> st(n);
while (q.size()) {
int u = q.front(); q.pop();
st[u] = 0;
for (auto [v, w] : e[u]) {
bool flag = false;
if (f[v][0] > f[u][0] + w) {
flag = true;
f[v][0] = f[u][0] + w;
}
for (int i = 1; i <= k; ++i) {
if (f[v][i] > f[u][i - 1]) {
f[v][i] = f[u][i - 1];
flag = true;
}
}
if (f[v][k] > f[u][k] + w) {
f[v][k] = f[u][k] + w;
flag = true;
}
if (flag && !st[v]) {
st[v] = 1;
q.push(v);
}
}
}
cout << min(f[n - 1][0], f[n - 1][k]) << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t = 1;
while (t--)
{
solve();
}
return 0;
}