题目：

给定一个非负整数 n，请计算 0 到 n 之间的每个数字的二进制表示中 1 的个数，并输出一个数组

示例：

1、

输入: n = 2
输出: [0,1,1]
解释: 
0 --> 0
1 --> 1
2 --> 10

2、

输入: n = 5
输出: [0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

解题思路：

1. 先把从 0 到 n 的非负整数，放到数组里
2. 把这些非负整数都转换为二进制
3. 判断他们当中 1 的个数
4. 把二进制中的 0 和 1 相加，然后输出成数组
5. 数组中数的和就是这些数当中 1 的个数

 

 

 

 

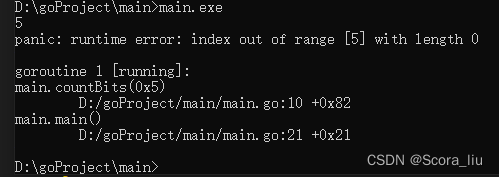
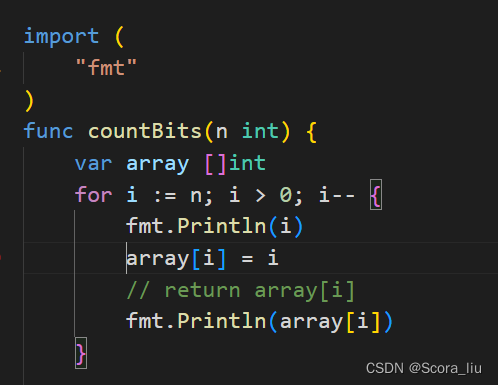
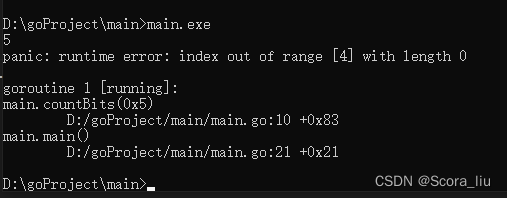
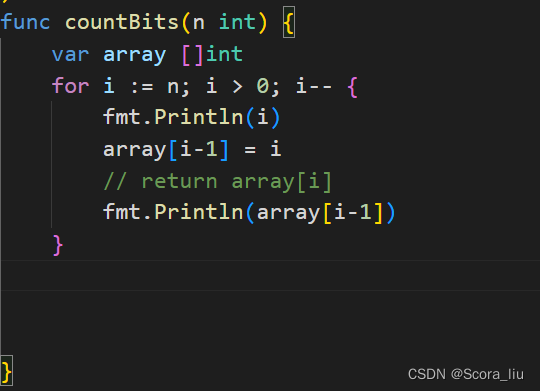
部分编程语言有相应的内置函数用于计算给定的整数的二进制表示中的 111 的数目，例如 Java\texttt{Java}Java 的 Integer.bitCount\texttt{Integer.bitCount}Integer.bitCount，C++\texttt{C++}C++ 的 __builtin_popcount\texttt{\_\_builtin\_popcount}__builtin_popcount，Go\texttt{Go}Go 的 bits.OnesCount\texttt{bits.OnesCount}bits.OnesCount 等，

方法一：Brian Kcrnighan 算法

最直观的做法是对从 0 到 n 的每个整数直接计算【一比特数】。每个 int 型的数都可以用 32 位二进制数表示，只有遍历其二进制表示的每一位即可得到 1 的数目。

利用 Brian Kcrnighan 算法，可以在一定程度上进一步提升计算速度。

Brian Kcrnighan算法的原理：

对于任意整数 x，令 x = x&(x - 1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则操作次数即为 x 的【一比特数】

 

func onesCount(x int) (ones int) {
	for ; x > 0; x &= x - 1 {
		ones++
	}
	return
}

func countBits(n int) []int {
	bits := make([]int, n+1)
	for i := range bits {
		bits[i] = onesCount(i)
	}
	return bits
}

 

方法二：动态规划 —— 最高有效位

func countBits(n int) []int {
	bits := make([]int, n+1)
	highBit := 0
	for i := 1, i <= n; i++ {
		if i&(i-1) == 0 {
			highBit = i
		}
		bits[i] = bits[i-highBit] + 1
	}
	return bits
}

 

 

 

方法三：动态规划 —— 最低有效位

 

 

func countBits(n int) []int {
	bits := make([]int, n+1)
	for i := 1; i <= n; i++ {
		bit[i] = bits[i>>1] + i&1
	}
	return bits
}

 

方法四：动态规划 —— 最低设置位

func countBits(n int) []int {
	bits := make([]int, n+1)
	for i := 1; i <= n; i++ {
		bits[i] = bits[i&(i-1)] + 1
	}
	return bits
}