设一元目标函数
f
(
x
)
f(x)
f(x)在区间
[
a
0
,
b
0
]
⊆
R
[a_0,b_0]\subseteq\text{R}
[a0,b0]⊆R(其长度记为
λ
\lambda
λ)上为单峰函数,且在
(
a
0
,
b
0
)
(a_0,b_0)
(a0,b0)内连续可导,即其导函数
f
′
(
x
)
f'(x)
f′(x)在
(
a
0
,
b
0
)
(a_0,b_0)
(a0,b0)内连续。在此增强的条件下,可以加速迭代计算压缩区间的过程。仍然设置计算精度为
ε
>
0
\varepsilon>0
ε>0。首次迭代,即
k
=
1
k=1
k=1时,插入点取
a
1
′
=
a
0
+
b
0
2
a'_1=\frac{a_0+b_0}{2}
a1′=2a0+b0。若
f
′
(
a
1
′
)
=
0
f'(a'_1)=0
f′(a1′)=0,即
a
1
′
a'_1
a1′为
f
(
x
)
f(x)
f(x)在
[
a
0
,
b
0
]
[a_0,b_0]
[a0,b0]的驻点,由单峰函数性质值,
a
1
′
a'_1
a1′为
f
(
x
)
f(x)
f(x)在
(
a
0
,
b
0
)
(a_0,b_0)
(a0,b0)内维一的极小值点
x
0
x_0
x0,停止迭代。否则,若
f
′
(
a
1
′
)
>
0
f'(a'_1)>0
f′(a1′)>0,意味着
f
(
x
)
f(x)
f(x)沿
a
1
′
a'_1
a1′的左边方向下降(见下图(a)),故
x
0
∈
(
a
0
,
a
1
′
)
x_0\in(a_0,a'_1)
x0∈(a0,a1′)。取压缩区间
[
a
1
,
b
1
]
=
[
a
0
,
a
1
′
]
[a_1,b_1]=[a_0,a'_1]
[a1,b1]=[a0,a1′]。若
f
′
(
a
1
′
)
<
0
f'(a'_1)<0
f′(a1′)<0,则
f
(
x
)
f(x)
f(x)沿
a
1
′
a'_1
a1′的右边方向下降(见下图(b)),必有
x
0
∈
(
a
1
′
,
b
0
)
x_0\in(a'_1,b_0)
x0∈(a1′,b0),取压缩区间为
[
a
1
,
b
1
]
=
[
a
1
′
,
b
0
]
[a_1,b_1]=[a'_1,b_0]
[a1,b1]=[a1′,b0]。无论哪种情形,
[
a
1
,
b
1
]
[a_1,b_1]
[a1,b1]的长度为
λ
/
2
\lambda/2
λ/2,即压缩比为
0.5
0.5
0.5。用此策略,继续迭代,直至得到
a
k
′
a'_k
ak′,使得
f
′
(
a
k
′
)
=
0
f'(a'_k)=0
f′(ak′)=0或
λ
/
2
k
<
ε
\lambda/2^k<\varepsilon
λ/2k<ε,停止迭代,
a
k
+
b
k
2
\frac{a_k+b_k}{2}
2ak+bk即为最小值点
x
0
x_0
x0的近似值。这一方法由于每次都将当前区间作对分,故称为“二分法”。回顾黄金分割法,迭代计算压缩区间的压缩比为
1
−
ρ
=
1
−
0.382
=
0.618
>
0.5
1-\rho=1-0.382=0.618>0.5
1−ρ=1−0.382=0.618>0.5,所以二分法比黄金分割法效率稍有提高。
将上述算法实现为如下的Python函数:
from scipy.optimize import OptimizeResult
bisection(fun,bracket,gtol,**options):
a0,b0=bracket #单峰区间端点
a1=(a0+b0)/2 #中点
f1,_=der_scalar(fun,a1) #中点处导数
k=1 #迭代次数
while abs(f1)>gtol: #重复迭代
k+=1
if f1<0: #导数为负
a0=a1 #修改左端点
else: #导数为正
b0=a1 #修改右端点
a1=(a0+b0)/2 #更新中点
f1,_=der_scalar(fun,a1) #更新中点处导数
bestx=a1
besty=fun(bestx)
return OptimizeResult(fun=besty, x=bestx, nit=k)
程序中第2-17行定义用二分策略计算目标函数局部最优解的bisection函数。参数fun表示目标函数
f
(
x
)
f(x)
f(x),bracket表示初始单峰区间
(
a
0
,
b
0
)
(a_0,b_0)
(a0,b0),gtol表示容错误差
ε
\varepsilon
ε,options用来使minimize_scalar将gtol等实际参数传递给bisection。第3行读取单峰区间(详见博文《连续函数的单峰区间计算》)左右端点a0和b0。第4行计算单峰区间的中点为a1。第5行调用der_scalar函数(详见博文《一元函数导数的数值计算》)计算
f
(
x
)
f(x)
f(x)在区间中点处的导数为f1。第6行将迭代次数k初始化为1。第7-14行的while循环执行重复迭代,直至当前区间中点处的导数绝对值接近0。循环体中,第8行迭代次数k自增1,第9~12行的if-else分支根据当前中点处导数的符号,决定下一次迭代的单峰区间。第13行更新当前区间中点,第14行更新中点处导数。第15、16行用a1分别设置最优解bestx和最优解处函数值besty。第17行用besty、bestx、k构造OptimizeResult对象并返回。
例1 用bisection函数计算函数
f
(
x
)
=
x
2
+
4
cos
x
f(x)=x^2+4\cos{x}
f(x)=x2+4cosx在
x
=
1
x=1
x=1附近的局部最优解。
解:下列代码计算本例。
import numpy as np
from scipy.optimize import minimize_scalar
f=lambda x:x**2+4*np.cos(x)
bracket=myBracket(f,1)
res=minimize_scalar(f,bracket,method=bisection, options={'eps':1.48e-8})
print(res)
程序很简单,第3行定义目标函数 f ( x ) f(x) f(x)为f。第4行调用myBracket函数计算 f ( x ) f(x) f(x)在 x = 1 x=1 x=1近旁的单峰区间。第5行调用scipy.optimize的minimize_scalar函数,传递f、bracket和bisection函数,计算 f ( x ) f(x) f(x)在 x = 1 x=1 x=1近旁的局部最优解。运行程序,输出
fun: 2.3168084197882135
nit: 26
x: 1.895494265556336
bisection以容错误差
ε
=
1.48
×
1
0
−
8
\varepsilon=1.48\times10^{-8}
ε=1.48×10−8,迭代26次,算得最优解近似值为1.895494265556336,最优解处函数近似值为2.3168084197882135。
例2 物资需从位于陆地的城市
A
A
A运送到位于水中的海岛
B
B
B,假定各点间距离如题图中所示,且物资在陆地及水中的运输速度分别为1和
1
2
\frac{1}{2}
21。试确定海岸线上码头建造位置
x
x
x,使得物资运输时间最短。
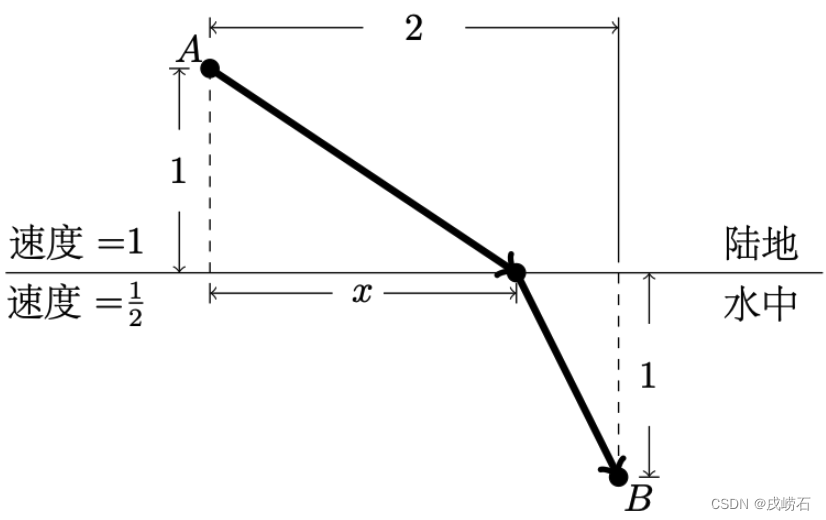
解:根据题意,算得目标函数(即物资运送时间)
f
(
x
)
=
1
+
x
2
+
2
1
+
(
2
−
x
)
2
f(x)=\sqrt{1+x^2}+2\sqrt{1+(2-x)^2}
f(x)=1+x2+21+(2−x)2,
0
≤
x
≤
2
0\leq x\leq2
0≤x≤2。解析方法解决此问题,需算得其导数
f
′
(
x
)
=
x
1
+
x
2
−
2
(
2
−
x
)
1
+
(
2
−
x
)
2
.
f'(x)=\frac{x}{\sqrt{1+x^2}}-\frac{2(2-x)}{\sqrt{1+(2-x)^2}}.
f′(x)=1+x2x−1+(2−x)22(2−x).
令其为0,算得驻点
x
0
x_0
x0。然后根据二阶导数
f
′
′
(
x
0
)
f''(x_0)
f′′(x0)的符号,判断
x
0
x_0
x0是否为极小值点。为求驻点
x
0
x_0
x0,需解方程
x
1
+
x
2
=
2
(
2
−
x
)
1
+
(
2
−
x
)
2
\frac{x}{\sqrt{1+x^2}}=\frac{2(2-x)}{\sqrt{1+(2-x)^2}}
1+x2x=1+(2−x)22(2−x)。这将导致解高次方程
3
x
4
−
12
x
3
+
15
x
2
−
16
x
+
16
=
0.
3x^4-12x^3+15x^2-16x+16=0.
3x4−12x3+15x2−16x+16=0.
手算的工作量极大。下面我们用黄金分割法数值地计算这个问题,代码如下。
import numpy as np #导入numpy
from scipy.optimize import minimize_scalar #导入minimize_scalar
f=lambda x:np.sqrt(1+x**2)+2*np.sqrt(1+(2-x)**2) #设置目标函数
bracket=myBracket(f, 0) #计算包围最优解的区间
res=minimize_scalar(f, bracket,method=bisection, #用二分法计算f(x)的最有接近似值
options={'eps':1.48e-8})
print(res)
程序第3行设置目标函数 f ( x ) f(x) f(x)。第4行调用myBracket函数计算0附近包围 f ( x ) f(x) f(x)最优解 x 0 x_0 x0的区间bracket。 第5~6行调用minimize_scalar函数,传递f、bracket、bisection以及提供给bisection的eps等参数,用二分法计算 f ( x ) f(x) f(x)的最优解近似值。运行程序,输出
fun: 4.037643276202614
nit: 23
x: 1.5382642555236816
意味着最优解 x 0 x_0 x0的近似值为1.5383, f ( x 0 ) f(x_0) f(x0)的近似值为4.0377。