线索二叉树

1 线索二叉树的基本概念

对一棵二叉树中所有结点的空指针域按照某种遍历方式加线索的过程叫作线索化，被线索化了的二叉树称为线索二叉树(Threaded binary tree)。

引入线索二叉树的目的是：加快查找结点前驱和后继的速度。

注：概念题也是会考的！( ^ ^)/~

2 线索二叉树的构造

2.1 线索二叉树的存储结构

图1 线索二叉树的结点结构

图1 ltag和rtag的设定

简单来说，ltag和rtag的作用：标明指针是否用作线索标志。

二叉树的存储结构代码描述如下：

typedef struct TBTNode{
	ElemType data;	//数据元素
	struct TBTNode *lchild, *rchild;	//左右孩子指针
	int ltag, rtag;		//左右线索标志
}TBTNode;

2.2 给线索二叉树画线索

2.2.1 中序

以下图的一棵二叉树为例，我们首先来讲解一下中序线索二叉树的建立过程：

图1 一棵二叉树

图2 在二叉树上添加中序线索

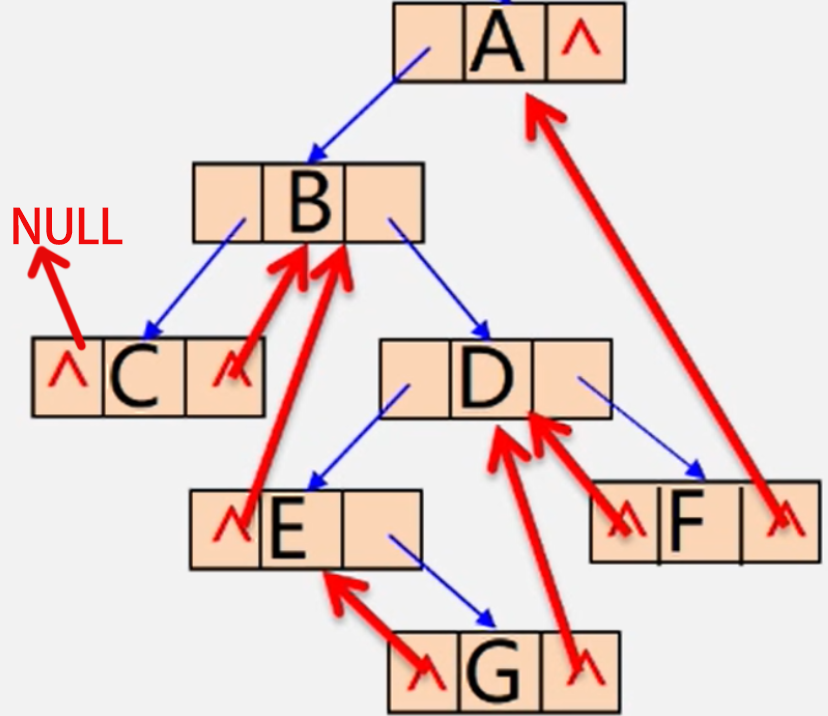
第一步，写出它的中序遍历序列，于是我们可以得到序列为：CBEGDFA。

第二步，根据中序序列，画出线索即可：

从中序遍历序列的第一个结点看起。也就是C结点，因为左右孩子均为空，所以得画上两条线索。因为中序序列CBEGDFA中，C前面没字母，换言之就是在中序序列中没有前驱，所以左边的线索指向NULL，而C的后面一个字母是B，故结点右边的线索指向B结点。

再来看E结点，因为左孩子为空，所以只需画上一条左边的线索。因为中序序列CBEGDFA中，E前面字母是B，换言之就是在中序序列中E的前驱结点是B，所以左边的线索指向B结点。

就这么简单~

2.2.2 先序

以下图的一棵二叉树为例，我们首先来讲解一下先序线索二叉树的建立过程：

图3 一棵二叉树

图4 添加先序线索

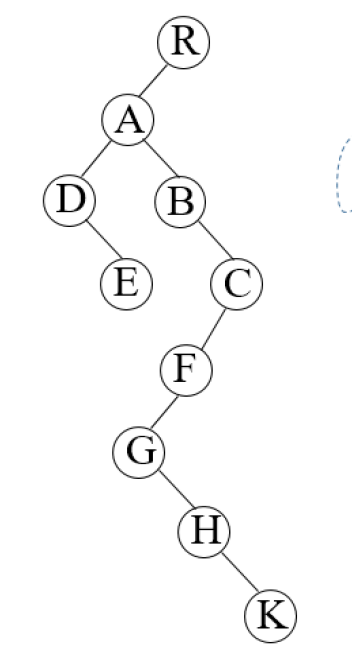
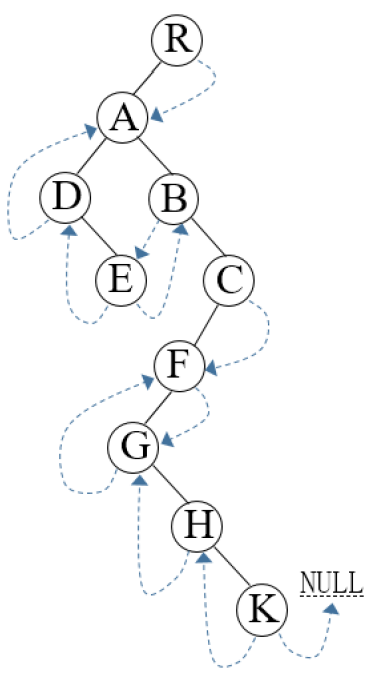
第一步，写出它的先序遍历序列，于是我们可以得到序列为：RADEBCFGHK。

然后根据遍历序列前后字母位置关系画线索即可。

2.2.3 后序

图5 一棵二叉树

图6 添加后序线索

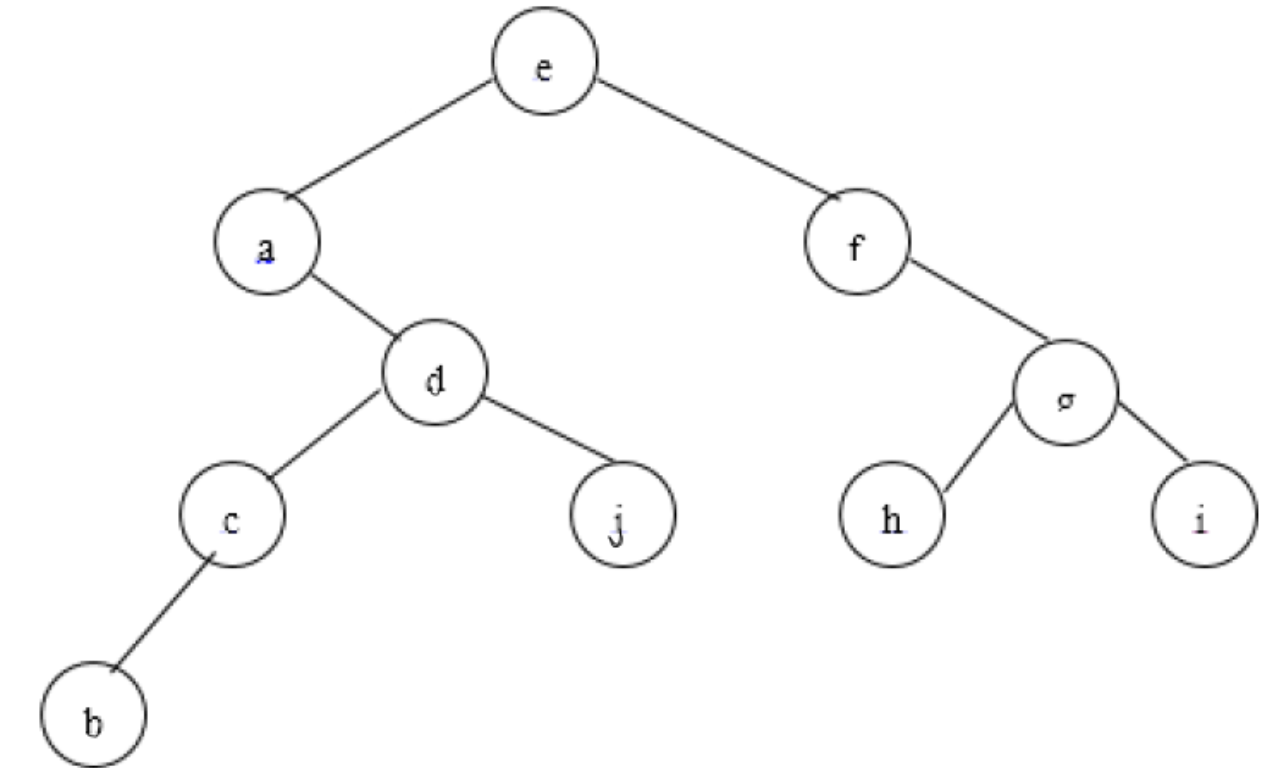
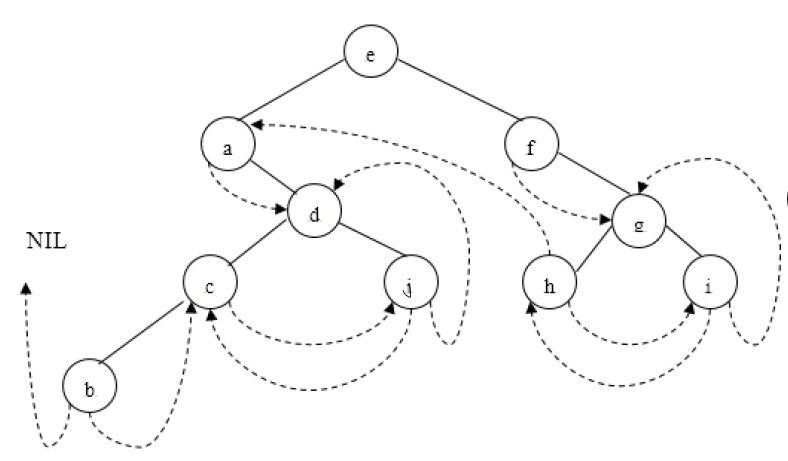
第一步，写出它的后序遍历序列，于是我们可以得到序列为：bcjdahigfe。

然后根据后序遍历序列顺序给空孩子添加前驱后继线索即可。

比如j结点，左右孩子为空，那么需添加两条线索。因为后序遍历序列中j前面是c，后面是d，于是j左线索指向c，右线索指向d。

2.3 二叉树线索化代码实现

2.3.1 通过中序遍历线索化

通过中序遍历对二叉树线索化的递归算法如下:

二叉树的存储结构代码：

typedef struct TBTNode{
	char data;	//数据元素
	struct TBTNode *lchild, *rchild;	//左右孩子指针
	int ltag, rtag;		//左右线索标志
}TBTNode;

主程序代码：

void createInThread(TBTNode *root){
    TBTNode *pre = NULL;   //前驱结点指针
    if(root != NULL){	
        InThread(root, pre);
        pre->rchild = NULL;	//处理中序最后的一个结点
        pre->rtag = 1；
    }
}

InThread部分：

void InThread(TBTNode *p, TBTNode *&pre){
    if(p != NULL){
        InThread(p->lchild, pre);  //递归，左子树线索化
        if(p->lchild == NULL){ //建立当前结点的前驱线索
            p->lchild = pre;
            p->ltag = 1;
        } 
        if(pre != NULL && pre->rchild == NULL){ //建立前驱结点的后继线索
            pre->rchild = p;
            pre->rtag = 1;
        }
	pre = p;	//标记当前结点，使其成刚刚访问过的结点
	InThread(p->rchild, pre);  //递归，右子树线索化
    }
}

注：TBTNode * &pre中，“ *& ”表示pre是一个指针类型的引用变量，即它可以引用一个TBTNode*类型的指针，并在函数内部修改所引用的指针的值，而这些修改也会反映到函数外部。由于使用了指针类型的引用变量pre来保存当前遍历节点的前驱节点，因此我们能够利用其记录已经遍历过的节点，在线索化二叉树时连接每个节点的前驱和后继指针。

【注意引用是C++语法，C是不支持的】

2.3.2 通过先序遍历线索化

void preThread(TBTNode *p, TBTNode *&pre){
    if(p != NULL){
        if(p->lchild == NULL){ //建立当前结点的前驱线索
            p->lchild = pre;
            p->ltag = 1;
        } 
        if(pre != NULL && pre->rchild == NULL){ //建立前驱结点的后继线索
            pre->rchild = p;
            pre->rtag = 1;
        }
	pre = p;	//标记当前结点，使其成刚刚访问过的结点
    if(p->ltag == 0)
        preThread(p->lchild, pre);
    if(p->rtag == 0)
        preThread(p->rchild, pre);
    }
}

注：为何这边要加上判断语句if(p->ltag == 0)和 if(p->rtag == 0)？

是为了避免重复遍历同一个结点。如果不判断左右孩子是否为线索，那么程序就有可能把线索也当成左右孩子来访问，从而导致重复遍历同一个结点(绕圈圈~)，最终导致栈溢出。

2.3.3 通过后序遍历线索化

void postThread(TBTNode *p, TBTNode *&pre){
    if(p != NULL){
        postThread(p->lchild, pre);  //递归左子树线索化
        postThread(p->lchild, pre);  //递归右子树线索化
        if(p->lchild == NULL){ //建立当前结点的前驱线索
            p->lchild = pre;
            p->ltag = 1;
        } 
        if(pre != NULL && pre->rchild == NULL){ //建立前驱结点的后继线索
            pre->rchild = p;
            pre->rtag = 1;
        }
	pre = p;	//标记当前结点，使其成刚刚访问过的结点
    }
}

3 线索二叉树的遍历

3.1 中序线索二叉树的遍历

第一步，编写一个方法，用来找出中序线索二叉树在中序序列中的第一个结点

TBTNode *First(TBTNode *p){
    while(p->ltag == 0) p = p->lchild;	//相当于找到树的最左下的结点
    return p;
}

第二步，编写一个方法，用来找出一个结点在中序序列中的后续结点

TBTNode *Next(TNTNode *p){
	if(p->rtag == 0){
		return First(p->rchild);
	}
	return p->rchild;		//rtag=1，直接返回后继线索rchild,因为线索化后，rchild就是线索了，指向后继结点
}

整合以上两个方法，即可得到中序线索二叉树的中序遍历算法

void Inorder(TBTNode *root){
    for(TBTNode *p = First(root); p != NULL; p = Next(p))
        Visit(p);	
}

3.2 先序线索二叉树的遍历

void preorder(TBTNode *root){
    if(root != NULL){
        TBTNode *p = root;
        while(p != NULL){
            while(p->ltag == 0){	//左指针不是线索
                Visit(p);
                p = p->lchild;	//那么边访问边向左移
            }
            Visit(p); //此时p左指针一定是线索，于是直接访问
            p = p->rchild	//此时p左孩子不存在，右指针无论是否是线索，都指向前序序列中的后继结点
        }
    }
}

3.3 后序线索二叉树的遍历

在考研数据结构中，只需记住以下三点，对代码要求不高(过于复杂)：

1. 若结点x是二叉树的根,则其后继为空。
2. 若结点x是其双亲的右孩子，或是其双亲的左孩子且其双亲没有右子树，则其后继即为双亲结点。
3. 若结点x是其双亲的左孩子，且其双亲有右子树，则其后继为双亲右子树上按后序遍历列出的第一个结点。

代码实现：因为在后序线索二叉树上找后继时，需要知道结点的双亲，所以需要带标志域的三叉链表作为存储结构。这里就不贴出代码了(因为考研不考 只需掌握思想即可)

4 补充知识点

线索二叉树的遍历无需使用栈，因为它利用了隐含在线索二叉树中的前驱和后继信息。线索二叉树相当于一个双向链表。