目录

频率响应法：

频率特性的概念：

一、频率特性的定义：

二、频率特性的求法:

三、频率特性的物理意义:

四、频率特性的图形表示方法:

---

频率响应法：

基本思想：通过开环频率特性的图形对系统进行分析。

主要优点：

（1）不求解闭环特征方程,可分析系统的稳定性；

（2）二阶系统频率特性与暂态性能指标有确切对应关系；

（3）频率响应有鲜明的物理意义（有效利用实验法）；

（4）不仅适用于线性系统，还可推广到非线性系统；

（5）可方便设计出能有效抑制噪声的系统。

---

频率特性的概念：

一、频率特性的定义：

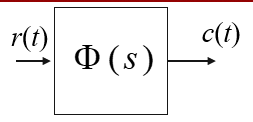
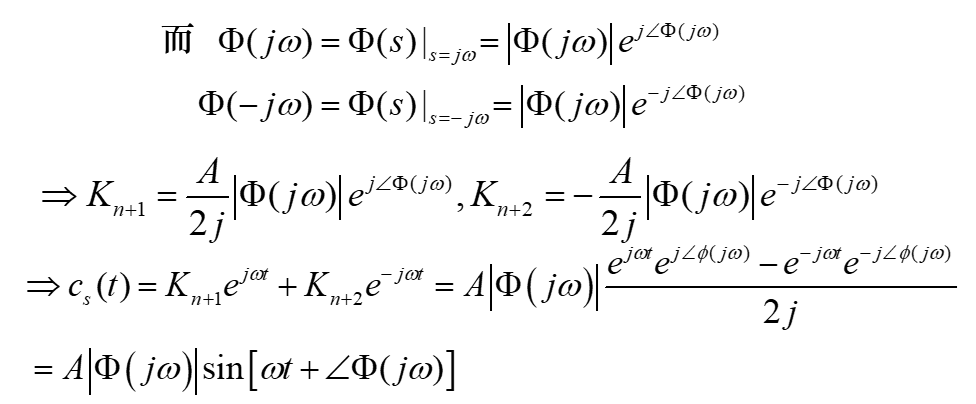
上述分析表明，对于稳定的线性定常系统，输入一个正弦信号，它的稳态响应是一个与输入同频率的正弦信号其幅值放大了倍，相位移动了 。

定义稳态响应的幅值与输入信号的幅值之比 ：

为系统的幅频特性，它描述系统对不同频率输入信号在稳态时的放大特性； 

定义稳态响应与正弦输入信号的相位差：

为系统的相频特性，它描述系统的稳态响应对不同频率输入信号的相位移特性；

频率特性函数的定义：零初始条件的线性系统或环节，在正弦信号作用下，稳态输出与输入的复数比，简称频率特性。表示为φ(jw)或G(jw)

频率特性与传递函数的关系:

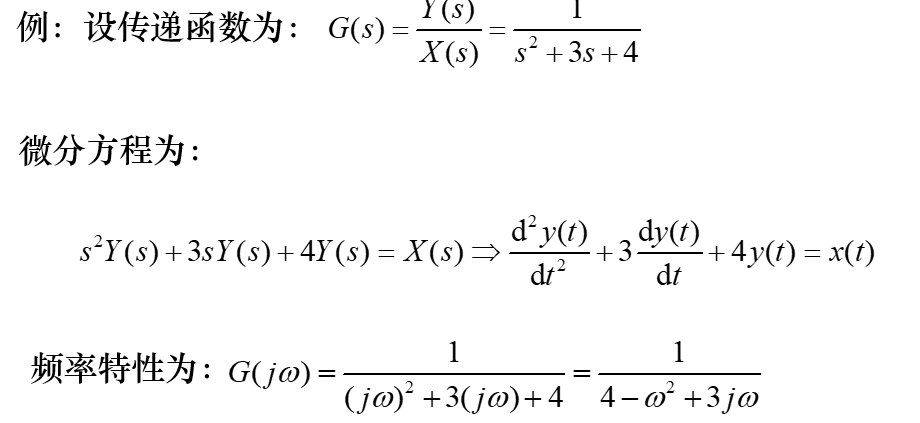
数学模型：微分方程、传递函数、脉冲（冲激）响应函数和频率特性。它们之间的关系如下：

---

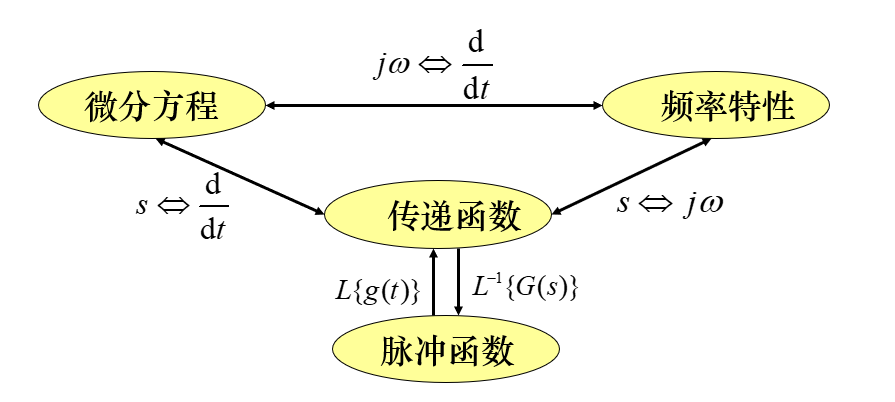
二、频率特性的求法:

已知系统的运动方程，输入正弦函数求其稳态解，取输出稳态分量和输入正弦的复数比。

 

---

三、频率特性的物理意义:

 

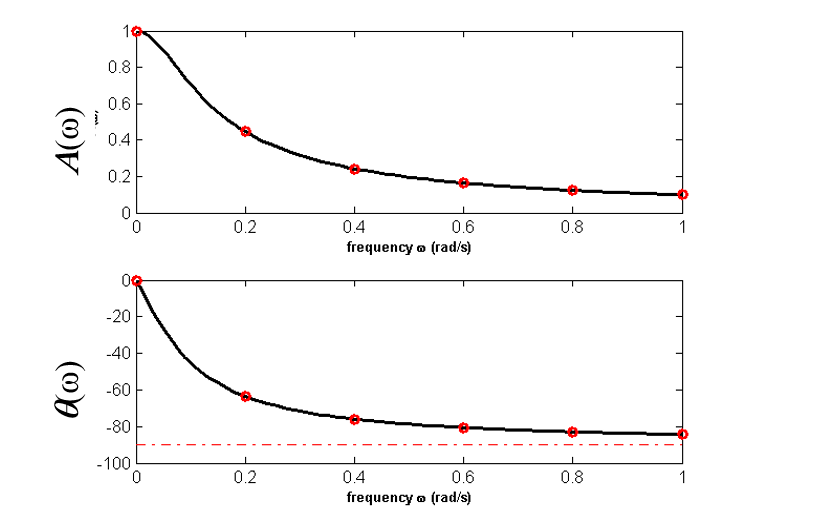
频率特性表征了系统或元件对不同频率正弦输入的响应特性

 

---

四、频率特性的图形表示方法:

1）对数频率特性图（Bode图）

2) 幅相频率特性图

（极坐标图或Nyquist图）

当w从0→+∞变化时，G(jw)的复向量轨迹图.

3）对数幅相频率特性图※（Nichols图 ）