基于NumPy构建LSTM模块并进行实例应用（附代码）

文章目录

- - 0. 前言
  - - 0.1 读本文前的必备知识
  - 1. LSTM架构
  - 2. LSTM正向传播代码实现
  - - 2.1 隐藏层正向传播
    - 2.2 输出层正向传播
  - 3. LSTM反向传播代码实现
  - - 3.1 输出层反向传播
    - 3.2 隐藏层反向传播
  - 4. 实例应用说明
  - 5. 运行结果
  - 6. 后记
  - 6 完整代码

0. 前言

按照国际惯例，首先声明：本文只是我自己学习的理解，虽然参考了他人的宝贵见解，但是内容可能存在不准确的地方。如果发现文中错误，希望批评指正，共同进步。

本篇文章的宗旨是：通过从零构建LSTM模块，并且应用于实例问题中来加深对LSTM（长短期记忆）神经元网络模型的学习及理解。

RNN与其他常见的神经元网络模型（FNN、CNN、GAN）相比，其数学算法底层是最为复杂的，而LSTM作为RNN的改进变体之一，把这个算法的复杂程度又提升了一个层次。因此有必要仔细学习下LSTM的算法及代码实现过程，以便能加强对LSTM的掌握程度以及做出更底层的算法创新。

0.1 读本文前的必备知识

本篇文章是基于Numpy构建RNN模块并进行实例应用（附代码）的姊妹篇。如果对RNN的底层算法实现不太了解，非常建议先学习下RNN的内容，否则很难看懂本篇文章；
LSTM（长短期记忆）网络的算法介绍及数学推导介绍了LSTM的底层数学算法（如果对于其数学推导过程难以理解，那只要知道其推导结果也可以），本文侧重是基于NumPy来从零构建LSTM，对于LSTM正向反向传播的数学公式会稍微带过。

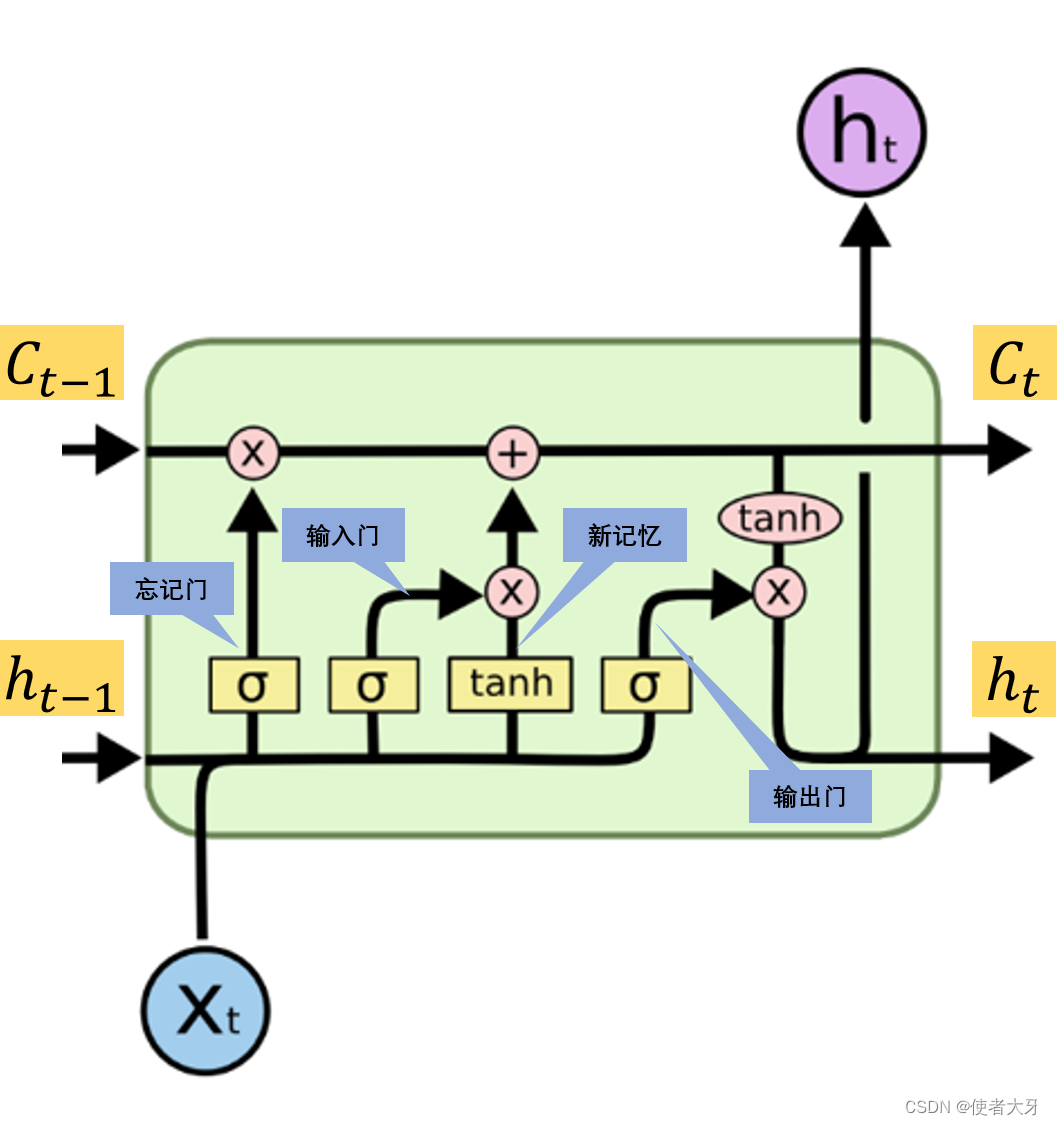
1. LSTM架构

其实这一块CSDN上有很多的介绍文章，以及colah的著名博客 Understanding LSTM Networks 都已经把LSTM的架构说的很明白了。但是我在编码的时候遇到了一些实际问题，所以还是把这块认真梳理一遍：

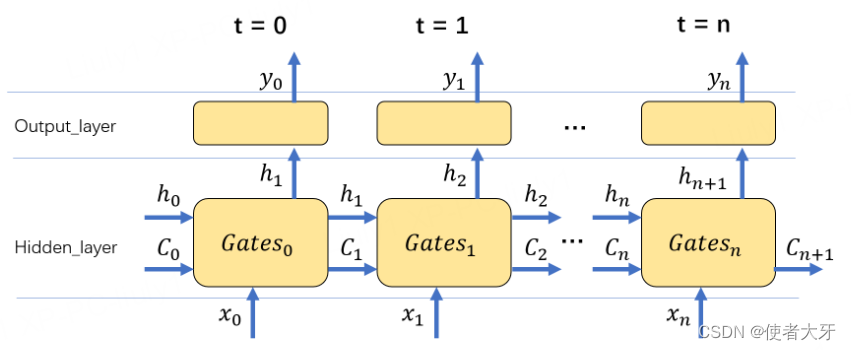
在这里插入图片描述
上面这个原理图说明了从0时刻到n时刻LSTM网络正向传播的过程，需要注意各个变量在每个时刻的序列，后面编码要严格按照这个序列进行。

细心的你或许已经发现这里把最后一个时刻输出的细胞状态 $C_{n+1}$ 也标了出来，后面也会说明这是因为在反向传播计算损失E对 $C_{n}$ 的偏导数时，需要使用到损失E对 $C_{n+1}$ 的偏导数进行反向迭代传播。

在LSTM内部的参数传递，仍然参照下面的原理图。

2. LSTM正向传播代码实现

正向传播都没有什么难度，只要严格按照上面的原理图进行即可

2.1 隐藏层正向传播

$t$ 时刻各个门为：

忘记门： $f_t = \sigma(w_f·x_t+v_f·h_{t-1}+b_f)$
输入门： $i_t = \sigma(w_i·x_t+v_i·h_{t-1}+b_i)$
新记忆门： $g_t = tanh(w_g·x_t+v_g·h_{t-1}+b_g)$
输出门： $o_t = \sigma(w_o·x_t+v_o·h_{t-1}+b_o)$

$t$ 时刻的细胞状态 $C_t$ 为：

$C_t = f_t \bigodot C_{t-1} + i_t \bigodot g_t$

$t$ 时刻的隐层输出 $h_t$ 为：

$h_t = o_t \bigodot tanh(C_t)$

代码实现：

  def forward(self, x, h_pre, c_pre):  #h_pre为h_t-1, c_pre为c_t-1

        self.Fgate = sigmoid(np.dot(self.w_f, x) + np.dot(self.v_f, h_pre) + self.b_f)
        self.Igate = sigmoid(np.dot(self.w_i, x) + np.dot(self.v_i, h_pre) + self.b_i)
        self.Ggate = np.tanh(np.dot(self.w_g, x) + np.dot(self.v_g, h_pre) + self.b_g)
        self.Ogate = sigmoid(np.dot(self.w_o, x) + np.dot(self.v_o, h_pre) + self.b_o)

        c_cur = self.Fgate * c_pre + self.Igate * self.Ggate  #c_cur为c_t
        h_cur = self.Ogate * np.tanh(c_cur)

        return h_cur, c_cur

这里可以通过多维列表节省一些代码行数，这里为了更清晰表明各个门，全部拆开来写。

2.2 输出层正向传播

$t$ 时刻的最终输出为：

$y_t = w_h·h_t + b_h$

输出层的正向传播公式一般写为 $y_t = softmax(w_h·h_t + b_h)$ ，这里能把softmax去掉就相当于把要学习的数据进行了一次逆softmax操作。

代码实现：

 def forward(self, h_cur):   #h_cur为 h_t
        return np.dot(self.w_h, h_cur) + self.b_h

3. LSTM反向传播代码实现

整个代码的难度都在反向传播这里。

3.1 输出层反向传播

这里损失的计算方式选用MSE(均方误差)来用代码实现，即 $E = 0.5*(y - y_{train})^2$ 。

这里前面增加一个0.5的系数是为了求导数时和平方项“2”抵消。

代码实现：

    def backward(self,y,h_cur, train_data):
        delta = y - train_data
        self.grad_wh = np.dot(delta, h_cur.T)
        self.grad_hcur = np.dot(self.w_h.T, delta)
        self.grad_bh = delta

在这段代码中，除了计算了损失 $E$ 对权重 $w_h$ 和 $b_h$ 的偏导，也对 $h$ 的偏导做了计算，这个会用于后面隐藏层权重偏导的计算。

3.2 隐藏层反向传播

这是整个LSTM算法中最核心、最难的部分。

在隐藏层的反向传播中，最关键的中间变量即是损失 $E$ 对细胞状态 $C_t$ 的偏导：

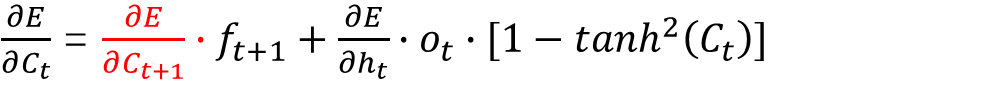
推导过程请见： LSTM（长短期记忆）网络的算法介绍及数学推导

式中 $\frac{\partial E}{\partial C_t}$ 通过下一时刻的 $\frac{\partial E}{\partial C_{t+1}}$ 迭代计算得出，这就要求在实际编码的时候增加一个变量存储每个时刻的 $\frac{\partial E}{\partial C_t}$ 。

而 $\frac{\partial E}{\partial h_t}$ 也是要通过迭代得出的，在 $t$ 时刻可以计算出 $\frac{\partial E}{\partial h_{t-1}}$ ，这个值也要存储起来，用于 $t - 1$ 时刻的反向传播计算用。

代码实现：

 def backward(self, Fgate, Igate, Ggate, Ogate, x, grad_cnext, Fgate_next, grad_hcur, c_cur,c_pre, h_pre):


        self.grad_ccur = grad_cnext * Fgate_next + grad_hcur * Ogate * (1 - np.tanh(c_cur) * np.tanh(c_cur))
        self.grad_hpre = self.grad_ccur*(np.dot(self.v_f.T, c_pre*Fgate*(1-Fgate)) + np.dot(self.v_g.T,Igate*(1-Ggate*Ggate)) + np.dot(self.v_i.T,Ggate*Igate*(1-Igate)))

        self.grad_wf = np.dot(self.grad_ccur * c_pre * Fgate * (1 - Fgate), x.T)  #这里要注意矩阵的转置!!!
        self.grad_wi = np.dot(self.grad_ccur * Ggate * Igate * (1 - Igate), x.T)
        self.grad_wg = np.dot(self.grad_ccur * Igate * (1 - Ggate * Ggate), x.T)
        self.grad_wo = np.dot(grad_hcur*np.tanh(c_cur)*Ogate*(1-Ogate),x.T)


        self.grad_vf = np.dot(self.grad_ccur * c_pre * Fgate * (1 - Fgate), h_pre.T)
        self.grad_vi = np.dot(self.grad_ccur * Ggate * Igate * (1 - Igate), h_pre.T)
        self.grad_vg = np.dot(self.grad_ccur * Igate * (1 - Ggate * Ggate), h_pre.T)
        self.grad_vo = np.dot(grad_hcur * np.tanh(c_cur) * Ogate * (1 - Ogate), h_pre.T)

        self.grad_bf = self.grad_ccur * c_pre * Fgate * (1 - Fgate)
        self.grad_bi = self.grad_ccur * Ggate * Igate * (1 - Igate)
        self.grad_bg = self.grad_ccur * Igate * (1 - Ggate * Ggate)
        self.grad_bo = grad_hcur * np.tanh(c_cur) * Ogate * (1 - Ogate)

4. 实例应用说明

本实例应用是拟合 $y = x^2$ 曲线，训练组输入数据train_x为0~1等间距取600个数据，每6个数据为1组，即100组数据。输出数据train_y为train_x的平方再加上一个随机噪声数据。
代码实现：

train_x = np.linspace(0.01,1,600).reshape(100,6,1)
train_y = train_x * train_x + np.random.randn(100,6,1)/200

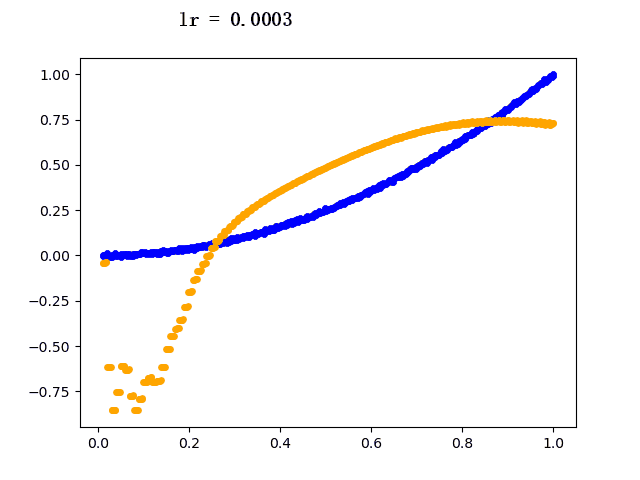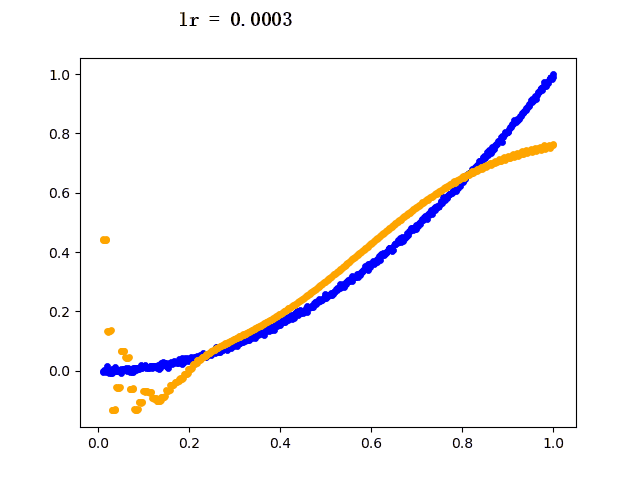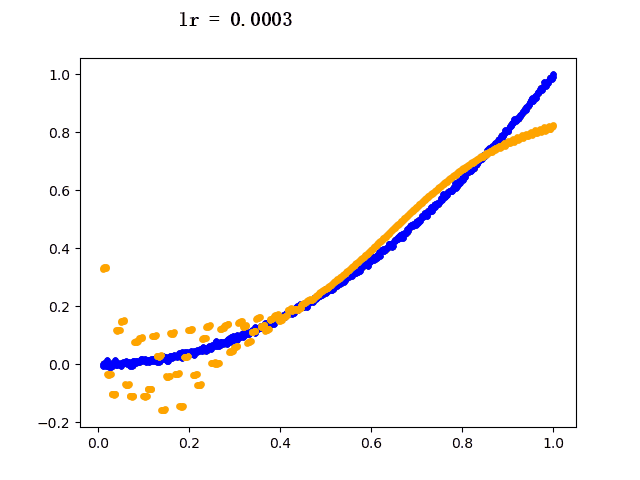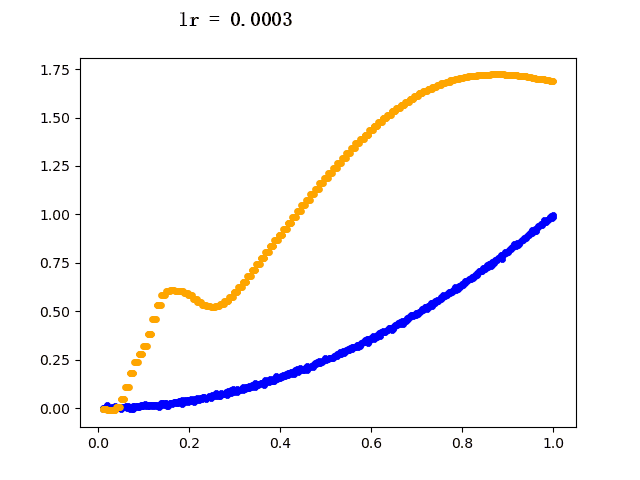
5. 运行结果

设定迭代次数epoch都为5000，选取不同的学习速率learning rate的模型学习过程如下（其中蓝色点为训练组数据，黄色点为网络模型输出数据）：

在这里插入图片描述

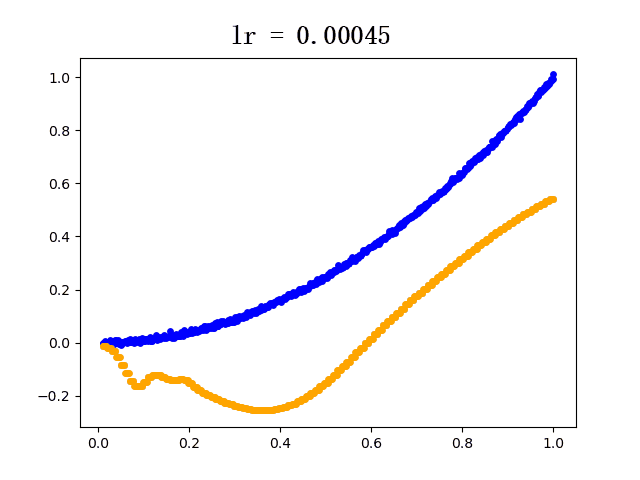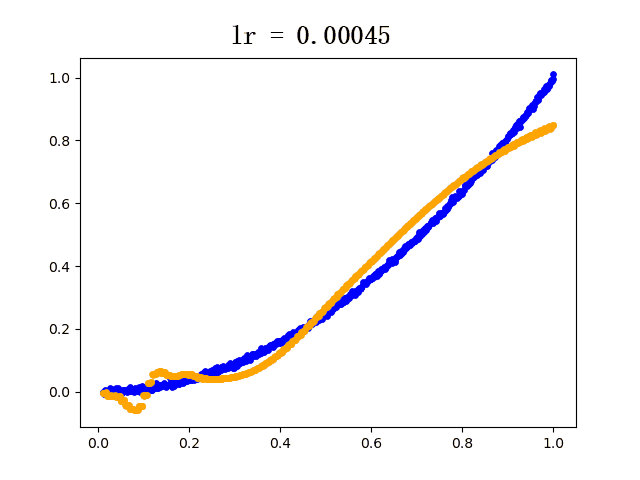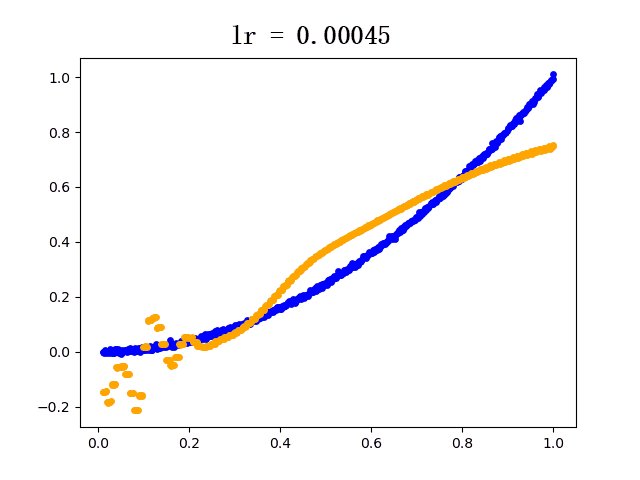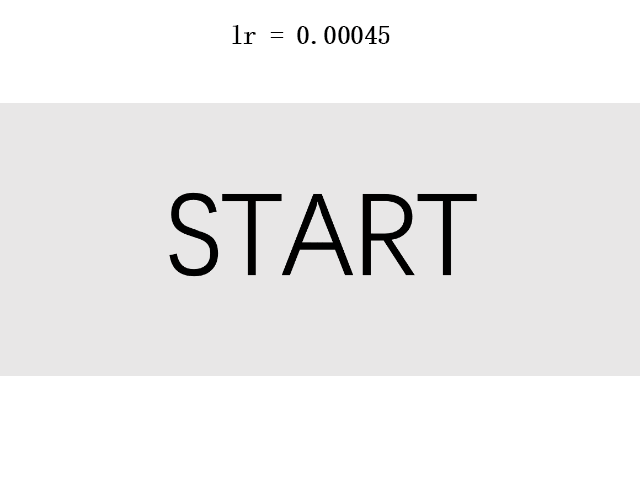
6. 后记

首先感谢能看到这里，整篇文章我陆陆续续编码+debug写了一个月，主要是隐藏层的反向传播部分确实不太好计算。在之前做LSTM数学推导时，我立了一个flag要用Python实现LSTM，也算是填了之前挖的坑，但是万万没想到LSTM的代码实现比RNN还要复杂的多。

而且在代码运行的时候非常容易发生计算溢出的问题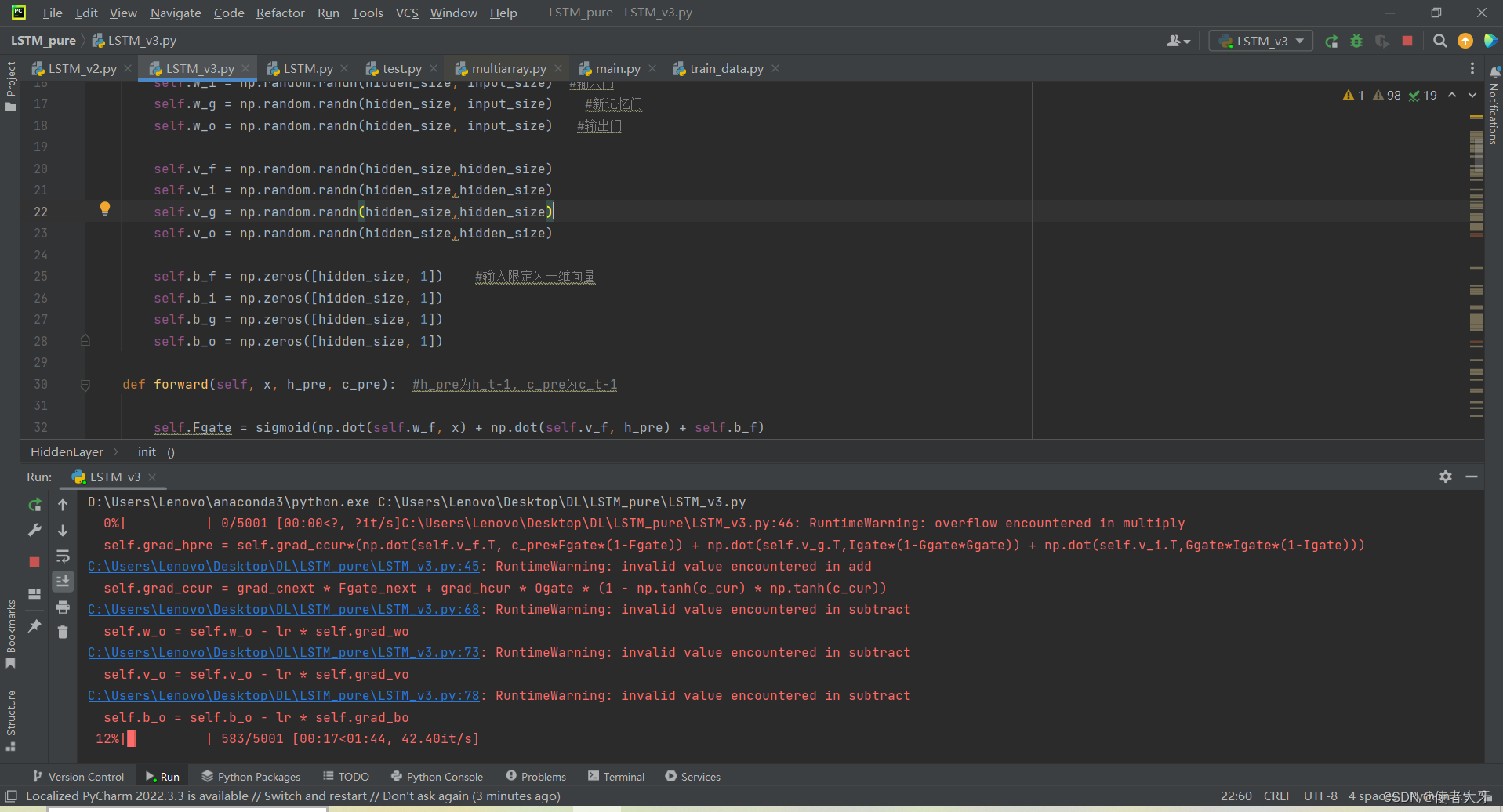：在这里插入图片描述
这种情况的输出肯定都是NaN，为此我尝试了很多解决方法都不灵，只能重新运行，期待下次计算不会溢出。

计算溢出的原因是梯度爆炸，梯度爆炸的原因我猜测是LSTM对权重的初始值有所“挑剔”，这个猜测的理由是代码运行只要顺利通过第一个epoch，后面便没问题了。

6 完整代码

import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt

train_x = np.linspace(0.01,1,600).reshape(100,6,1)
train_y = train_x * train_x + np.random.randn(100,6,1)/200


def sigmoid(x):
    return 1/(1+np.exp(-x))


class HiddenLayer():
    def __init__(self,input_size, hidden_size):
        self.w_f = np.random.randn(hidden_size, input_size) #定义各个门的权重, 忘记门
        self.w_i = np.random.randn(hidden_size, input_size)  #输入门
        self.w_g = np.random.randn(hidden_size, input_size)    #新记忆门
        self.w_o = np.random.randn(hidden_size, input_size)   #输出门

        self.v_f = np.random.randn(hidden_size,hidden_size)
        self.v_i = np.random.randn(hidden_size,hidden_size)
        self.v_g = np.random.randn(hidden_size,hidden_size)
        self.v_o = np.random.randn(hidden_size,hidden_size)

        self.b_f = np.zeros([hidden_size, 1])    #输入限定为一维向量
        self.b_i = np.zeros([hidden_size, 1])
        self.b_g = np.zeros([hidden_size, 1])
        self.b_o = np.zeros([hidden_size, 1])

    def forward(self, x, h_pre, c_pre):  #h_pre为h_t-1, c_pre为c_t-1

        self.Fgate = sigmoid(np.dot(self.w_f, x) + np.dot(self.v_f, h_pre) + self.b_f)
        self.Igate = sigmoid(np.dot(self.w_i, x) + np.dot(self.v_i, h_pre) + self.b_i)
        self.Ggate = np.tanh(np.dot(self.w_g, x) + np.dot(self.v_g, h_pre) + self.b_g)
        self.Ogate = sigmoid(np.dot(self.w_o, x) + np.dot(self.v_o, h_pre) + self.b_o)

        c_cur = self.Fgate * c_pre + self.Igate * self.Ggate  #c_cur为c_t
        h_cur = self.Ogate * np.tanh(c_cur)

        return h_cur, c_cur

    def backward(self, Fgate, Igate, Ggate, Ogate, x, grad_cnext, Fgate_next, grad_hcur, c_cur,c_pre, h_pre):


        self.grad_ccur = grad_cnext * Fgate_next + grad_hcur * Ogate * (1 - np.tanh(c_cur) * np.tanh(c_cur))
        self.grad_hpre = self.grad_ccur*(np.dot(self.v_f.T, c_pre*Fgate*(1-Fgate)) + np.dot(self.v_g.T,Igate*(1-Ggate*Ggate)) + np.dot(self.v_i.T,Ggate*Igate*(1-Igate)))

        self.grad_wf = np.dot(self.grad_ccur * c_pre * Fgate * (1 - Fgate), x.T)  #这里要注意矩阵的转置!!!
        self.grad_wi = np.dot(self.grad_ccur * Ggate * Igate * (1 - Igate), x.T)
        self.grad_wg = np.dot(self.grad_ccur * Igate * (1 - Ggate * Ggate), x.T)
        self.grad_wo = np.dot(grad_hcur*np.tanh(c_cur)*Ogate*(1-Ogate),x.T)


        self.grad_vf = np.dot(self.grad_ccur * c_pre * Fgate * (1 - Fgate), h_pre.T)
        self.grad_vi = np.dot(self.grad_ccur * Ggate * Igate * (1 - Igate), h_pre.T)
        self.grad_vg = np.dot(self.grad_ccur * Igate * (1 - Ggate * Ggate), h_pre.T)
        self.grad_vo = np.dot(grad_hcur * np.tanh(c_cur) * Ogate * (1 - Ogate), h_pre.T)

        self.grad_bf = self.grad_ccur * c_pre * Fgate * (1 - Fgate)
        self.grad_bi = self.grad_ccur * Ggate * Igate * (1 - Igate)
        self.grad_bg = self.grad_ccur * Igate * (1 - Ggate * Ggate)
        self.grad_bo = grad_hcur * np.tanh(c_cur) * Ogate * (1 - Ogate)

    def step(self, lr=0.01):
        self.w_f = self.w_f - lr * self.grad_wf
        self.w_i = self.w_i - lr * self.grad_wi
        self.w_g = self.w_g - lr * self.grad_wg
        self.w_o = self.w_o - lr * self.grad_wo

        self.v_f = self.v_f - lr*self.grad_vf
        self.v_i = self.v_i - lr * self.grad_vi
        self.v_g = self.v_g - lr * self.grad_vg
        self.v_o = self.v_o - lr * self.grad_vo

        self.b_f = self.b_f - lr*self.grad_bf
        self.b_i = self.b_i - lr * self.grad_bi
        self.b_g = self.b_g - lr * self.grad_bg
        self.b_o = self.b_o - lr * self.grad_bo


class OutputLayer():
    def __init__(self, hidden_size, output_size):

        self.w_h = np.ones([output_size, hidden_size])
        self.b_h = np.zeros([output_size, 1])

    def forward(self, h_cur):
        return np.dot(self.w_h, h_cur) + self.b_h

    def backward(self,y,h_cur, train_data):
        delta = y - train_data
        self.grad_wh = np.dot(delta, h_cur.T)
        self.grad_hcur = np.dot(self.w_h.T, delta)
        self.grad_bh = delta

    def step(self, lr=0.001):
        self.w_h = self.w_h - lr * self.grad_wh
        self.b_h = self.b_h - lr * self.grad_bh

#---------------------------------------------------
LstmHidden = HiddenLayer(6, 10)
LstmOut = OutputLayer(10, 6)

Fgate_data = np.zeros([101,10,1])  #这些都是要存储的数据
Igate_data = np.zeros([100,10,1])
Ggate_data = np.zeros([100,10,1])
Ogate_data = np.zeros([100,10,1])
gradc_data = np.zeros([101,10,1])  #这里是101是因为c和h都多一个第0时刻的数据
gradh_data = np.zeros([101,10,1])
c_data = np.zeros([101,10,1])
h_data = np.zeros([101,10,1])
y = np.zeros([100,6,1])

epoch = 5001
total_time = len(train_x)

for e in tqdm(range(epoch)):
    for t in range(total_time):

        h_data[t + 1],c_data[t + 1] = LstmHidden.forward(train_x[t], h_data[t], c_data[t])
        Fgate_data[t] = LstmHidden.Fgate
        Igate_data[t] = LstmHidden.Igate
        Ggate_data[t] = LstmHidden.Ggate
        Ogate_data[t] = LstmHidden.Ogate


        y[t] = LstmOut.forward(h_data[t + 1])




    LstmOut.backward(y[total_time-1], h_data[total_time], train_y[total_time-1])
    gradh_data[total_time]=LstmOut.grad_hcur
    gradc_data[total_time] =gradh_data[total_time]  * Ogate_data[total_time-1]* (1 - c_data[total_time] * c_data[total_time])

    LstmOut.backward(y[total_time-2], h_data[total_time-1], train_y[total_time-2])
    gradh_data[total_time-1]=LstmOut.grad_hcur

    for t in reversed(range(total_time-1)):
        LstmOut.backward(y[t], h_data[t + 1], train_y[t])

        LstmHidden.backward(Fgate_data[t],Igate_data[t],Ggate_data[t],Ogate_data[t],train_x[t],
                            gradc_data[t+2],Fgate_data[t+1], gradh_data[t+1], c_data[t+1], c_data[t], h_data[t])
        gradc_data[t+1] = LstmHidden.grad_ccur
        gradh_data[t] = LstmHidden.grad_hpre


        LstmHidden.step(lr=0.00037)
        LstmOut.step(lr=0.00037)

    if e%200 == 0 :
        plt.clf()
        plt.scatter(train_x, train_y, c="blue", s=15)  # 蓝色线为真实值
        plt.scatter(train_x, y, c="orange", s=15)  # 黄色线为预测值
        plt.savefig('x^2_epoch5000_lr00037_%s'%e)


loss = (y-train_y)**2

print(loss)