R中的方差分析
介绍用于比较独立组的不同类型的方差分析,包括:
- 单因素方差分析:独立样本 t 检验的扩展,用于在存在两个以上组的情况下比较均值。这是方差分析检验的最简单情况,其中数据仅根据一个分组变量(也称为因子变量)组织成多个组。其他同义词是:1 方式方差分析、单因素方差分析和主体间方差分析。
- 双向方差分析用于同时评估两个不同分组变量对连续结果变量的影响。其他同义词是:双因子设计、因子方差分析或双向主体间方差分析。
- 三因素方差分析用于同时评估三个不同分组变量对连续结果变量的影响。其他同义词是:阶乘方差分析或三向主体间方差分析。
请注意,独立分组变量也称为主体间因子。双向和三向方差分析的主要目标分别是评估在解释连续结果变量时,两个和三个主体间因子之间是否存在统计学上显着的交互作用效应。
学习内容:
- 计算和解释 R 中不同类型的方差分析,以比较独立组。
- 检查方差分析检验假设
- 执行事后测试,组之间的多个成对比较,以确定哪些组不同
- 使用箱形图可视化数据,将方差分析和成对比较 p 值添加到图中
基本
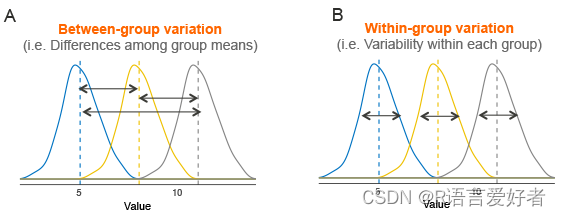
假设我们有 3 组要比较,如下图所示。虚线表示组均值。该图显示了组均值(面板 A)和每个组内的变化(面板 B)之间的变异,也称为残差方差。
方差分析检验背后的想法非常简单:如果组间的平均变异与组内的平均变异相比足够大,那么您可以得出结论,至少一个组均值不等于其他组均值。
因此,可以通过比较两个方差估计来评估组均值之间的差异是否显著。这就是为什么该方法被称为方差分析,即使主要目标是比较组均值。
简而言之,方差分析检验背后的数学过程如下:
- 计算组内方差,也称为残差方差。这告诉我们,每个参与者与他们自己的小组平均值有多大不同(见图,面板B)。
- 计算组均值之间的方差(见图,面板 A)。
- 将 F 统计量生成为 的比率。variance.between.groups/variance.within.groups
请注意,较低的 F 值 (F < 1) 表示所比较样本的均值之间没有显著差异。然而,较高的比率意味着与每个组中单个观测值的变异相比,组均值之间的变异彼此之间存在很大差异。
假设
方差分析检验对数据做出以下假设:
- 观察的独立性。每个主题只能属于一个组。每个组中的观测值之间没有关系。不允许对相同的参与者重复采取措施。
- 设计的任何单元中都没有明显的异常值
- 常态。每个设计单元的数据应近似呈正态分布。
- 方差的同质性。结果变量的方差在设计的每个单元格中应相等。
在计算方差分析检验之前,您需要执行一些初步检验以检查是否满足假设。
请注意,如果不满足上述假设,则存在单因子方差分析的非参数替代方案(Kruskal-Wallis 检验)。不幸的是,没有双向和三向方差分析的非参数替代方案。因此,在不满足假设的情况下,您可以考虑对变换数据和非变换数据运行双向/三向方差分析,以查看是否存在任何有意义的差异。如果两个检验都得出相同的结论,则可能不会选择变换结果变量并继续对原始数据进行双向/三向方差分析。也可以使用 WRS2 R 包执行稳健的方差分析测试。无论您的选择如何,您都应该报告您在结果中做了什么。
先决条件
请确保具有以下 R 包:
- tidyverse用于数据操作和可视化
- ggpubr用于创建易于发布的绘图
- rstatix提供管道友好型 R 函数,便于统计分析
- datarium:包含本章所需的数据集
加载所需的 R 包: