题目描述

 

 

 

原文链接

题目链接 

上面中文总结一下：

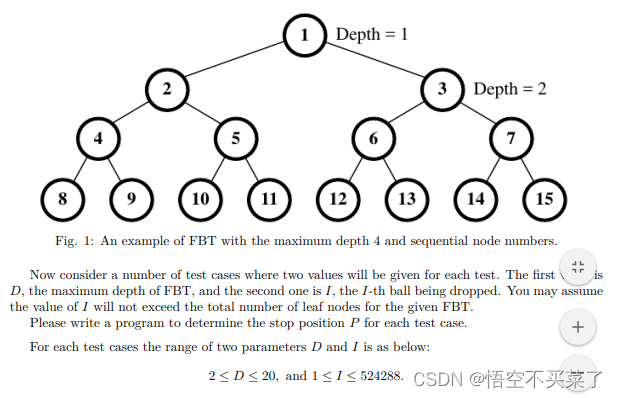
D代表这棵树深度，那么一共就有2^d -1 个结点

每个结点从左到右，从上往下，从1开始递增编号，那么也就是说对于结点k来说，左子结点与右子结点的编号分别为2k和2k+1。

现在是放一些小球从结点1开始往下面掉，我们要输出第I个小球的位置，也就是最后一个小球落到叶子结点的位置。

条件：

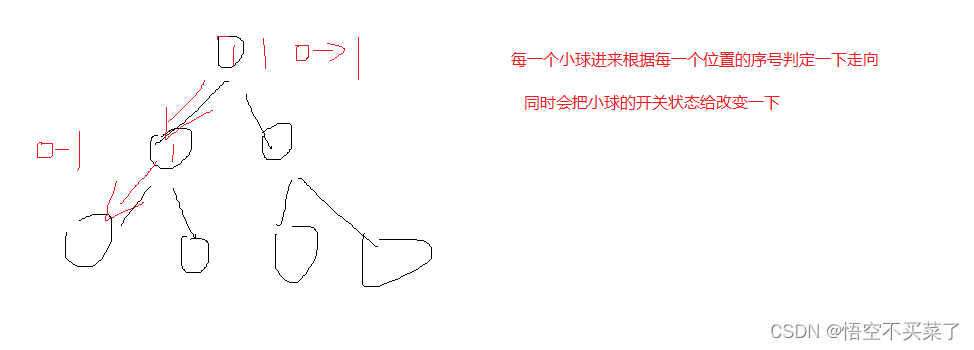
在初始状态下，每一个结点是处于关闭状态，这里可以用0来表示，当一个球落到这个结点上的时候，结点状态可能改变，但是这个改变不一定是从0到1，也有可能之前打开过是1，然后又变成0，至于为什么要说这个，是因为，他会判定出小球的走向，比如当结点=0的时候，往左走，否则就往右边走。

题目分析

这里给出两种题解分析

第一种：直接根据走向进行判定往那边走，也就是说这里根据序号来进行判定

根据每一个小球序号判定，但是当数据量特别大的时候，就很容易出现问题

第二种：根据奇偶性来判定一下 一下小球的走向

这个思路也算是比较简单，如果这个结点是偶数次的路过这个结点，那么小球肯定是往右边走，因为奇数的时候已经把结点的状态从0变为了1。如果是奇数，那么这个结点肯定被偶数的时候从1变成了0，又回到最初状态。

这里也就是说，如果结点是i%2=1,说明i是一个奇数球，这个球，会走左边，毕竟是0，那么它的下一个结点位置就是k=2k,左边，那么让它的下一个位置结点判定是奇数次还是偶数次，就是i = （i+1）/2，如果是奇数走左边，偶数右边

偶数直接i = i/2

代码实现

先是第一种方法的实现

demo1.cpp

#include <cstdio>
#include <cstring>

//这里对D有个限制条件就是D<=20
//我们建立一个在节点上的一个判定数组
//这个数组保存这个结点的开和关
const int maxd = 20;
int s[1<<maxd];//最大结点个数为2^maxd - 1,k是从1开始的
int total_num;//定义一次输入几组测试数据

int main()
{
	int D,I;//一个层数，一个小球的下落个数，一个小球落之后在落下一个小球
	int flag;
	scanf("%d",&total_num);
	//开始循环输入的几组数据
	while(total_num--) {
		scanf("%d %d",&D,&I);
		//把一片内存空间进行初始化操作
		memset(s,0,sizeof(s));
		int k,n = (1<<D) - 1;//n是这棵树最大的一个结点编号
		//开始连续让小球下落
		for(int i = 0;i < I;i++) {
			k = 1;//从第一个结点开始下落
			//每一个球开始往下面落的过程
			for(;;) {
				//这个球走到这个结点，会把这个结点的状态改变掉
				//我们要去判定的不是改变之后的状态，而是之前的转态判断走向
				//改变k的值，当k处于0关闭的时候，往左走
				s[k] = !s[k];
				//k会改变，所以之前先把k的状态改变一下
				k = s[k] ? k*2 : k*2+1;
				if(k > n) break;//大于最大的结点编号
				}
			}
			printf("%d\n",k/2);
		}
	return 0;
}

 然后是第二种方法实现

#include <cstdio>
#include <cstdlib>


using namespace std;



int D,I,k;//需要这棵树的层数，小球总个数，k表示结点的位置

int main()
{
	int total_number;
	scanf("%d",&total_number);
	while(total_number--) {
		scanf("%d %d",&D,&I);
		//直接用I的奇偶性进行判断
		k = 1;//从第一个结点位置开始往下面移动
		//这里还是要经历一个循环
		//但是只用循环到d-1层，就可以判定数据最后落定的数
		for(int i = 1;i <= D-1;i++) {
			if(I % 2 == 1) {
				//奇数位置
				//往左边走，老规矩，0
				k *= 2;
				//判定走完之后的下一个位置
				I = (I + 1) / 2;
			} else {
				//说明是偶数
				//往右边走为1
				k = 2*k + 1;
				I = I / 2;
			}
 
		}
		//上面循环完之后，k也就到了一个正确的位置
		printf("%d\n",k);
	}
	return 0;
}