文章目录
- 1.2 有限元分析的数学原理
- 1.2.1 基于最小势能原理的变分法提法
- 1.2.1.a 弹性力学方程简化记法
- 1.2.1.b 应变能密度和应变余能密度
- 1.2.1.c 最小势能原理变分基础
1.2 有限元分析的数学原理
书接上回,我们已经回顾了线性有限元分析的理论基础——线弹性力学的内容,虽然有限元方法本质上等效于弹性力学方程的数值解法,但是有限元方法毕竟不是差分法,它并不直接离散控制方程,而是通过等效于控制方程的另一种形式来实现的。这种形式可以是加权残值法或者虚功原理,亦或者是最小势能原理。这几种方法本质上可以互相转换。在本文中,我们选择最小势能原理来说明线性有限元分析方法的一般流程。
1.2.1 基于最小势能原理的变分法提法
1.2.1.a 弹性力学方程简化记法
最小势能原理是一个物理学普遍性的原理,物质系统经过一系列的作用,最终达到的平衡状态一定是总体势能处于最小的状态。力学系统的最小势能原理可以表述为:力学系统所有的可能位移中,真实发生的位移,一定是使力学系统势能取到最小。
回顾上篇,弹性静力学的所有求解方程和边界如下所示
{
平衡方程:
{
∂
σ
x
x
(
x
,
y
,
z
)
∂
x
+
∂
τ
x
y
(
x
,
y
,
z
)
∂
y
+
∂
τ
x
z
(
x
,
y
,
z
)
∂
z
+
b
x
=
0
∂
τ
y
x
(
x
,
y
,
z
)
∂
x
+
∂
σ
y
y
(
x
,
y
,
z
)
∂
y
+
∂
τ
y
z
(
x
,
y
,
z
)
∂
z
+
b
y
=
0
∂
τ
z
x
(
x
,
y
,
z
)
∂
x
+
∂
τ
z
y
(
x
,
y
,
z
)
∂
y
+
∂
σ
z
z
(
x
,
y
,
z
)
∂
z
+
b
z
=
0
几何方程:
{
ε
x
x
=
∂
u
∂
x
ε
y
y
=
∂
v
∂
y
ε
z
z
=
∂
w
∂
z
γ
x
y
=
∂
v
∂
x
+
∂
u
∂
y
γ
y
z
=
∂
w
∂
y
+
∂
v
∂
z
γ
z
x
=
∂
w
∂
x
+
∂
u
∂
z
本构方程:
{
ε
x
=
σ
x
E
−
μ
(
σ
y
E
+
σ
z
E
)
ε
y
=
σ
y
E
−
μ
(
σ
x
E
+
σ
z
E
)
ε
z
=
σ
z
E
−
μ
(
σ
x
E
+
σ
y
E
)
γ
x
y
=
τ
x
y
G
γ
y
z
=
τ
y
z
G
γ
z
x
=
τ
z
x
G
边界条件:
{
S
u
上有
{
u
=
u
^
v
=
v
^
w
=
w
^
S
p
上有:
{
σ
x
x
⋅
n
x
−
τ
z
x
⋅
n
z
−
τ
y
x
⋅
n
y
=
P
x
σ
y
y
⋅
n
y
−
τ
z
y
⋅
n
x
−
τ
x
y
⋅
n
z
=
P
y
σ
z
z
⋅
n
z
−
τ
y
x
⋅
n
z
−
τ
x
z
⋅
n
y
=
P
z
(1-29)
\begin{cases}平衡方程:\begin{cases} \frac{\partial\sigma_{xx}(x,y,z)}{\partial x} + \frac{\partial \tau_{xy}(x,y,z)}{\partial y} + \frac{\partial\tau_{xz}(x,y,z)}{\partial z} +b_x= 0\\ \frac{\partial\tau_{yx}(x,y,z)}{\partial x} + \frac{\partial \sigma_{yy}(x,y,z)}{\partial y} + \frac{\partial\tau_{yz}(x,y,z)}{\partial z} +b_y=0\\ \frac{\partial\tau_{zx}(x,y,z)}{\partial x} + \frac{\partial \tau_{zy}(x,y,z)}{\partial y} + \frac{\partial\sigma_{zz}(x,y,z)}{\partial z} +b_z= 0 \end{cases}\\ 几何方程: \begin{cases} \varepsilon_{xx}=\frac{\partial u}{\partial x} \\ \varepsilon_{yy}=\frac{\partial v}{\partial y} \\ \varepsilon_{zz}=\frac{\partial w}{\partial z} \\ \gamma_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\\ \gamma_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\\ \gamma_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\end{cases}\\ 本构方程:\begin{cases} \varepsilon_x=\frac{\sigma_{x}}{E}-\mu(\frac{\sigma_{y}}{E}+\frac{\sigma_{z}}{E}) \\ \varepsilon_y=\frac{\sigma_{y}}{E}-\mu(\frac{\sigma_{x}}{E}+\frac{\sigma_{z}}{E}) \\ \varepsilon_z=\frac{\sigma_{z}}{E}-\mu(\frac{\sigma_{x}}{E}+\frac{\sigma_{y}}{E}) \\ \gamma_{xy}=\frac{\tau_{xy}}{G}\\ \gamma_{yz}=\frac{\tau_{yz}}{G}\\ \gamma_{zx}=\frac{\tau_{zx}}{G}\end{cases}\\ 边界条件:\begin{cases}S_u上有 \begin{cases} u=\hat u\\ v=\hat v\\ w=\hat w \end{cases}\\ S_p上有:\begin{cases} \sigma_{xx}\cdot n_x-\tau_{zx}\cdot n_z-\tau_{yx}\cdot n_y=P_{x}\\ \sigma_{yy}\cdot n_y-\tau_{zy}\cdot n_x-\tau_{xy}\cdot n_z=P_{y}\\ \sigma_{zz}\cdot n_z-\tau_{yx}\cdot n_z-\tau_{xz}\cdot n_y=P_{z} \end{cases}\end{cases}\end{cases} \tag{1-29}
⎩
⎨
⎧平衡方程:⎩
⎨
⎧∂x∂σxx(x,y,z)+∂y∂τxy(x,y,z)+∂z∂τxz(x,y,z)+bx=0∂x∂τyx(x,y,z)+∂y∂σyy(x,y,z)+∂z∂τyz(x,y,z)+by=0∂x∂τzx(x,y,z)+∂y∂τzy(x,y,z)+∂z∂σzz(x,y,z)+bz=0几何方程:⎩
⎨
⎧εxx=∂x∂uεyy=∂y∂vεzz=∂z∂wγxy=∂x∂v+∂y∂uγyz=∂y∂w+∂z∂vγzx=∂x∂w+∂z∂u本构方程:⎩
⎨
⎧εx=Eσx−μ(Eσy+Eσz)εy=Eσy−μ(Eσx+Eσz)εz=Eσz−μ(Eσx+Eσy)γxy=Gτxyγyz=Gτyzγzx=Gτzx边界条件:⎩
⎨
⎧Su上有⎩
⎨
⎧u=u^v=v^w=w^Sp上有:⎩
⎨
⎧σxx⋅nx−τzx⋅nz−τyx⋅ny=Pxσyy⋅ny−τzy⋅nx−τxy⋅nz=Pyσzz⋅nz−τyx⋅nz−τxz⋅ny=Pz(1-29)
为了简化公式和方便形式运算,我们引入Einstein标记法来简化公式,Einstein标记法具体使用方法如下:
a
1
b
1
+
a
2
b
2
+
a
3
b
3
=
∑
i
=
1
3
a
i
b
i
=
E
i
n
s
t
e
i
n
a
i
b
i
(1-30)
a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=\sum_{i=1}^3 a_{i}b_{i}\xlongequal{Einstein}{}a_{i}b_{i}\tag{1-30}
a1b1+a2b2+a3b3=i=1∑3aibiEinsteinaibi(1-30)
a
11
b
1
+
a
12
b
2
+
a
13
b
3
=
∑
i
=
1
3
a
1
i
b
i
a
21
b
1
+
a
22
b
2
+
a
23
b
3
=
∑
i
=
1
3
a
2
i
b
i
a
31
b
1
+
a
32
b
2
+
a
33
b
3
=
∑
i
=
1
3
a
3
i
b
i
}
=
a
j
i
b
i
=
a
i
j
b
j
(1-31)
\left . \begin{aligned} a_{11}b_{1}+a_{12}b_{2}+a_{13}b_{3}=\sum_{i=1}^3 a_{1i}b_{i}\\ a_{21}b_{1}+a_{22}b_{2}+a_{23}b_{3}=\sum_{i=1}^3 a_{2i}b_{i}\\ a_{31}b_{1}+a_{32}b_{2}+a_{33}b_{3}=\sum_{i=1}^3 a_{3i}b_{i} \end{aligned} \right \} \large\xlongequal{} a_{ji}b_{i}=a_{ij}b_{j}\tag{1-31}
a11b1+a12b2+a13b3=i=1∑3a1ibia21b1+a22b2+a23b3=i=1∑3a2ibia31b1+a32b2+a33b3=i=1∑3a3ibi⎭
⎬
⎫ajibi=aijbj(1-31)
我们把公式(1-30)中
a
i
b
i
a_{i}b_{i}
aibi的
i
i
i、公式(1-31)中
a
j
i
b
i
a_{ji}b_{i}
ajibi的
i
i
i和
a
i
j
b
j
a_{ij}b_{j}
aijbj的
j
j
j称为哑指标,可以看到哑指标是可以替换标记号的。
应用Einstein标记法来简化公式得到平衡方程
∂
σ
x
x
(
x
,
y
,
z
)
∂
x
+
∂
τ
x
y
(
x
,
y
,
z
)
∂
y
+
∂
τ
x
z
(
x
,
y
,
z
)
∂
z
+
b
x
=
0
∂
τ
y
x
(
x
,
y
,
z
)
∂
x
+
∂
σ
y
y
(
x
,
y
,
z
)
∂
y
+
∂
τ
y
z
(
x
,
y
,
z
)
∂
z
+
b
y
=
0
∂
τ
z
x
(
x
,
y
,
z
)
∂
x
+
∂
τ
z
y
(
x
,
y
,
z
)
∂
y
+
∂
σ
z
z
(
x
,
y
,
z
)
∂
z
+
b
z
=
0
⟹
∂
σ
x
1
x
1
∂
x
1
+
∂
σ
x
1
x
2
∂
x
2
+
∂
σ
x
1
x
2
∂
x
3
+
b
x
1
=
0
∂
σ
x
2
x
1
∂
x
1
+
∂
σ
x
2
x
2
∂
x
2
+
∂
σ
x
2
x
3
∂
x
3
+
b
x
2
=
0
∂
σ
x
3
x
1
∂
x
1
+
∂
σ
x
3
x
2
∂
x
2
+
∂
σ
x
3
x
3
∂
x
3
+
b
x
3
=
0
}
⟹
∂
σ
i
j
∂
x
j
+
b
i
=
0
(
1
−
32
)
\begin{aligned} \begin{aligned}\frac{\partial\sigma_{xx}(x,y,z)}{\partial x} + \frac{\partial \tau_{xy}(x,y,z)}{\partial y} + \frac{\partial\tau_{xz}(x,y,z)}{\partial z} +b_x= 0\\\frac{\partial\tau_{yx}(x,y,z)}{\partial x} + \frac{\partial \sigma_{yy}(x,y,z)}{\partial y} + \frac{\partial\tau_{yz}(x,y,z)}{\partial z} +b_y= 0\\ \frac{\partial\tau_{zx}(x,y,z)}{\partial x} + \frac{\partial \tau_{zy}(x,y,z)}{\partial y} + \frac{\partial\sigma_{zz}(x,y,z)}{\partial z} +b_z= 0 \end{aligned} \Longrightarrow \left .\begin{aligned}\frac{\partial\sigma_{x_{1}x_{1}}}{\partial x_{1}} + \frac{\partial \sigma_{x_{1}x_{2}}}{\partial x_{2}} + \frac{\partial\sigma_{x_{1}x_{2}}}{\partial x_{3}} +b_{x_{1}}=0\\ \frac{\partial\sigma_{x_{2}x_{1}}}{\partial x_{1}} + \frac{\partial \sigma_{x_{2}x_{2}}}{\partial x_{2}} + \frac{\partial\sigma_{x_{2}x_{3}}}{\partial x_{3}} +b_{x_{2}}= 0\\ \frac{\partial\sigma_{x_{3}x_{1}}}{\partial x_{1}} + \frac{\partial \sigma_{x_{3}x_{2}}}{\partial x_{2}} + \frac{\partial\sigma_{x_{3}x_{3}}}{\partial x_{3}} +b_{x_{3}}= 0 \end{aligned}\right\} \Longrightarrow \frac{\partial\sigma_{ij}}{\partial{x_{j}}}+b_i=0\\ (1-32)\end{aligned}
∂x∂σxx(x,y,z)+∂y∂τxy(x,y,z)+∂z∂τxz(x,y,z)+bx=0∂x∂τyx(x,y,z)+∂y∂σyy(x,y,z)+∂z∂τyz(x,y,z)+by=0∂x∂τzx(x,y,z)+∂y∂τzy(x,y,z)+∂z∂σzz(x,y,z)+bz=0⟹∂x1∂σx1x1+∂x2∂σx1x2+∂x3∂σx1x2+bx1=0∂x1∂σx2x1+∂x2∂σx2x2+∂x3∂σx2x3+bx2=0∂x1∂σx3x1+∂x2∂σx3x2+∂x3∂σx3x3+bx3=0⎭
⎬
⎫⟹∂xj∂σij+bi=0(1−32)
其中
(
x
,
y
,
z
)
=
记为
(
x
1
,
x
2
,
x
3
)
(x,y,z)\xlongequal{记为}(x_{1},x_{2},x_{3})
(x,y,z)记为(x1,x2,x3),
σ
x
i
x
j
=
记为
σ
i
j
\sigma_{x_{i}x_{j}}\xlongequal{记为}\sigma_{ij}
σxixj记为σij,
b
x
3
=
记为
b
3
b_{x_{3}}\xlongequal{记为}b_{3}
bx3记为b3。
应用Einstein标记法来简化几何方程,如下式所示。
ε
x
x
=
∂
u
∂
x
ε
y
y
=
∂
v
∂
y
ε
z
z
=
∂
w
∂
z
γ
x
y
=
(
∂
v
∂
x
+
∂
u
∂
y
)
γ
y
z
=
(
∂
w
∂
y
+
∂
v
∂
z
)
γ
z
x
=
(
∂
w
∂
x
+
∂
u
∂
z
)
⟹
ε
x
x
=
1
2
(
∂
u
1
∂
x
1
+
∂
u
1
∂
x
1
)
ε
y
y
=
1
2
(
∂
u
2
∂
x
2
+
∂
u
2
∂
x
2
)
ε
z
z
=
1
2
(
∂
u
3
∂
x
3
+
∂
u
3
∂
x
3
)
ε
x
y
=
1
2
(
∂
u
2
∂
x
1
+
∂
u
1
∂
x
2
)
ε
y
z
=
1
2
(
∂
u
3
∂
x
2
+
∂
u
2
∂
x
3
)
ε
z
x
=
1
2
(
∂
u
3
∂
x
1
+
∂
u
1
∂
x
3
)
}
⟹
ε
i
j
=
1
2
(
∂
u
i
∂
x
j
+
∂
u
j
∂
x
i
)
(1-33)
\begin{aligned} \varepsilon_{xx}=\frac{\partial u}{\partial x} \\ \varepsilon_{yy}=\frac{\partial v}{\partial y} \\ \varepsilon_{zz}=\frac{\partial w}{\partial z} \\ \gamma_{xy}=(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y})\\ \gamma_{yz}=(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})\\ \gamma_{zx}=(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}) \end{aligned} \Longrightarrow \left . \begin{aligned} \varepsilon_{xx}=\frac{1}{2}(\frac{\partial u_{1}}{\partial x_{1}}+\frac{\partial u_{1}}{\partial x_{1}}) \\ \varepsilon_{yy}=\frac{1}{2}(\frac{\partial u_{2}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{2}}) \\ \varepsilon_{zz}=\frac{1}{2}(\frac{\partial u_{3}}{\partial x_{3}}+\frac{\partial u_{3}}{\partial x_{3}}) \\ \varepsilon_{xy}=\frac{1}{2}(\frac{\partial u_{2}}{\partial x_{1}}+\frac{\partial u_{1}}{\partial x_{2}})\\ \varepsilon_{yz}=\frac{1}{2}(\frac{\partial u_{3}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{3}})\\ \varepsilon_{zx}=\frac{1}{2}(\frac{\partial u_{3}}{\partial x_{1}}+\frac{\partial u_{1}}{\partial x_{3}}) \end{aligned} \right\}\Longrightarrow \varepsilon_{ij}=\frac{1}{2}(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}})\tag{1-33}
εxx=∂x∂uεyy=∂y∂vεzz=∂z∂wγxy=(∂x∂v+∂y∂u)γyz=(∂y∂w+∂z∂v)γzx=(∂x∂w+∂z∂u)⟹εxx=21(∂x1∂u1+∂x1∂u1)εyy=21(∂x2∂u2+∂x2∂u2)εzz=21(∂x3∂u3+∂x3∂u3)εxy=21(∂x1∂u2+∂x2∂u1)εyz=21(∂x2∂u3+∂x3∂u2)εzx=21(∂x1∂u3+∂x3∂u1)⎭
⎬
⎫⟹εij=21(∂xj∂ui+∂xi∂uj)(1-33)
其中
ε
i
j
=
1
2
γ
i
j
(
i
≠
j
)
\varepsilon_{ij}=\frac{1}{2}\gamma_{ij}(i\neq j)
εij=21γij(i=j),这样记主要为了统一表达式,此外这样记录有利于后续应变能密度表达方便。
对本构方程进行变换,如下式所示。
ε
x
=
σ
x
E
−
μ
(
σ
y
E
+
σ
z
E
)
ε
y
=
σ
y
E
−
μ
(
σ
x
E
+
σ
z
E
)
ε
z
=
σ
z
E
−
μ
(
σ
x
E
+
σ
y
E
)
γ
x
y
=
τ
x
y
G
γ
y
z
=
τ
y
z
G
γ
z
x
=
τ
z
x
G
⟹
σ
x
x
=
E
(
1
−
2
μ
)
(
1
+
μ
)
[
(
1
+
μ
)
ε
x
x
+
μ
(
ε
y
y
+
ε
z
z
)
]
σ
y
y
=
E
(
1
−
2
μ
)
(
1
+
μ
)
[
(
1
+
μ
)
ε
y
y
+
μ
(
ε
x
x
+
ε
z
z
)
]
σ
z
z
=
E
(
1
−
2
μ
)
(
1
+
μ
)
[
(
1
+
μ
)
ε
z
z
+
μ
(
ε
x
x
+
ε
y
y
)
]
σ
x
y
=
2
G
ε
x
y
σ
y
z
=
2
G
ε
y
z
σ
z
x
=
2
G
ε
z
x
(1-34)
\begin{aligned} \varepsilon_x=\frac{\sigma_{x}}{E}-\mu(\frac{\sigma_{y}}{E}+\frac{\sigma_{z}}{E}) \\ \varepsilon_y=\frac{\sigma_{y}}{E}-\mu(\frac{\sigma_{x}}{E}+\frac{\sigma_{z}}{E}) \\ \varepsilon_z=\frac{\sigma_{z}}{E}-\mu(\frac{\sigma_{x}}{E}+\frac{\sigma_{y}}{E}) \\ \gamma_{xy}=\frac{\tau_{xy}}{G}\\ \gamma_{yz}=\frac{\tau_{yz}}{G}\\ \gamma_{zx}=\frac{\tau_{zx}}{G} \end{aligned} \Longrightarrow \begin{aligned} \sigma_{xx}=\frac{E}{(1-2\mu)(1+\mu)}[(1+\mu)\varepsilon_{xx}+\mu(\varepsilon_{yy}+\varepsilon_{zz})] \\ \sigma_{yy}=\frac{E}{(1-2\mu)(1+\mu)}[(1+\mu)\varepsilon_{yy}+\mu(\varepsilon_{xx}+\varepsilon_{zz})] \\ \sigma_{zz}=\frac{E}{(1-2\mu)(1+\mu)}[(1+\mu)\varepsilon_{zz}+\mu(\varepsilon_{xx}+\varepsilon_{yy})] \\ \sigma_{xy}=2G\varepsilon_{xy}\\ \sigma_{yz}=2G\varepsilon_{yz}\\ \sigma_{zx}=2G\varepsilon_{zx} \end{aligned}\tag{1-34}
εx=Eσx−μ(Eσy+Eσz)εy=Eσy−μ(Eσx+Eσz)εz=Eσz−μ(Eσx+Eσy)γxy=Gτxyγyz=Gτyzγzx=Gτzx⟹σxx=(1−2μ)(1+μ)E[(1+μ)εxx+μ(εyy+εzz)]σyy=(1−2μ)(1+μ)E[(1+μ)εyy+μ(εxx+εzz)]σzz=(1−2μ)(1+μ)E[(1+μ)εzz+μ(εxx+εyy)]σxy=2Gεxyσyz=2Gεyzσzx=2Gεzx(1-34)
将应力分量和应变分量组成列阵,那么上式右边写成矩阵形式
[
σ
x
x
σ
y
y
σ
z
z
σ
x
y
σ
y
z
σ
z
z
]
=
[
E
1
−
2
μ
E
μ
(
1
−
2
μ
)
(
1
+
μ
)
E
μ
(
1
−
2
μ
)
(
1
+
μ
)
E
μ
(
1
−
2
μ
)
(
1
+
μ
)
E
1
−
2
μ
E
μ
(
1
−
2
μ
)
(
1
+
μ
)
E
μ
(
1
−
2
μ
)
(
1
+
μ
)
E
μ
(
1
−
2
μ
)
(
1
+
μ
)
E
1
−
2
μ
2
G
0
0
0
2
G
0
0
0
2
G
]
⋅
[
ε
x
x
ε
y
y
ε
z
z
ε
x
y
ε
y
z
ε
z
z
]
(1-35)
\begin{bmatrix} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ \sigma_{xy}\\ \sigma_{yz}\\ \sigma_{zz}\\ \end{bmatrix}= \begin{bmatrix} \frac{E}{1-2\mu} & \frac{E\mu}{(1-2\mu)(1+\mu)} & \frac{E\mu}{(1-2\mu)(1+\mu)}\\ \frac{E\mu}{(1-2\mu)(1+\mu)} & \frac{E}{1-2\mu} & \frac{E\mu}{(1-2\mu)(1+\mu)} \\ \frac{E\mu}{(1-2\mu)(1+\mu)} & \frac{E\mu}{(1-2\mu)(1+\mu)} & \frac{E}{1-2\mu} \\ 2G & 0 & 0\\ 0 & 2G & 0\\ 0 & 0 & 2G\\ \end{bmatrix}\cdot \begin{bmatrix} \varepsilon_{xx} \\ \varepsilon_{yy} \\ \varepsilon_{zz} \\ \varepsilon_{xy}\\ \varepsilon_{yz}\\ \varepsilon_{zz}\\ \end{bmatrix}\tag{1-35}
σxxσyyσzzσxyσyzσzz
=
1−2μE(1−2μ)(1+μ)Eμ(1−2μ)(1+μ)Eμ2G00(1−2μ)(1+μ)Eμ1−2μE(1−2μ)(1+μ)Eμ02G0(1−2μ)(1+μ)Eμ(1−2μ)(1+μ)Eμ1−2μE002G
⋅
εxxεyyεzzεxyεyzεzz
(1-35)
当然事实上,一点的应力状态是由各应力分量组成的应力张量描述,应力张量(二阶张量)可以用矩阵来表示
[
σ
x
x
σ
x
y
σ
x
z
σ
y
x
σ
y
y
σ
y
z
σ
z
x
σ
z
y
σ
z
z
]
(1-36)
\begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz}\\ \end{bmatrix}\tag{1-36}
σxxσyxσzxσxyσyyσzyσxzσyzσzz
(1-36)
同理,一点的应变状态是由各应变分量组成的应变张量描述,应变张量(二阶张量)可以用矩阵来表示
[
ε
x
x
ε
x
y
ε
x
z
ε
y
x
ε
y
y
ε
y
z
ε
z
x
ε
z
y
ε
z
z
]
(1-37)
\begin{bmatrix} \varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz}\\ \varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz}\\ \varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz}\\ \end{bmatrix}\tag{1-37}
εxxεyxεzxεxyεyyεzyεxzεyzεzz
(1-37)
应力应变之间的关系此时已经不能用矩阵表示了,因为两者之间的相差一个四阶张量,只能用分量的形式表示,同时应用Einstein标记法,并将应力应变关系系数记为
D
i
j
k
l
D_{ijkl}
Dijkl,那么应力应变关系也就是本构关系如下式所示。
σ
i
j
=
D
i
j
k
l
ε
k
l
(
=
∑
k
∑
l
D
i
j
k
l
ε
k
l
)
(1-38)
\sigma_{ij}=D_{ijkl}\varepsilon_{kl}(=\sum^k\sum^lD_{ijkl}\varepsilon_{kl})\tag{1-38}
σij=Dijklεkl(=∑k∑lDijklεkl)(1-38)
同理,边界条件可以简化为如下所示。
在
S
u
上
:
u
i
=
u
^
i
在
S
p
上
:
σ
i
j
n
j
=
p
i
(1-39)
\begin{aligned} 在S_{u}上&:u_{i}=\hat u_{i}\\ 在S_{p}上&:\sigma_{ij}n_{j}=p_{i}\end{aligned} \tag{1-39}
在Su上在Sp上:ui=u^i:σijnj=pi(1-39)
综上,弹性静力学基本方程可以简化为下式。
{
平衡方程:
∂
σ
i
j
∂
x
j
+
b
i
=
0
几何方程:
ε
i
j
=
1
2
(
∂
u
i
∂
x
j
+
∂
u
j
∂
x
i
)
本构方程:
σ
i
j
=
D
i
j
k
l
ε
k
l
边界条件:
{
S
u
上有
:
u
i
=
u
^
i
S
p
上有:
σ
i
j
n
j
=
p
i
(1-40)
\begin{cases}平衡方程:\frac{\partial\sigma_{ij}}{\partial{x_{j}}}+b_i=0\\ 几何方程:\varepsilon_{ij}=\frac{1}{2}(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}) \\ 本构方程:\sigma_{ij}=D_{ijkl}\varepsilon_{kl}\\ 边界条件:\begin{cases}S_u上有: u_{i}=\hat u_{i}\\ S_p上有:\sigma_{ij}n_{j}=p_{i}\end{cases}\end{cases} \tag{1-40}
⎩
⎨
⎧平衡方程:∂xj∂σij+bi=0几何方程:εij=21(∂xj∂ui+∂xi∂uj)本构方程:σij=Dijklεkl边界条件:{Su上有:ui=u^iSp上有:σijnj=pi(1-40)
1.2.1.b 应变能密度和应变余能密度
在用最小势能原理前,我们需要先了解物体的应变能(应变势能或形变能等),首先我们引入一维杆为例,如下图1.2.1,图中一维杆原长 l l l 截面面积A受到F的拉力,最终伸长了 u 0 u_{0} u0。那么结构的外力功可以建立如下式(1-41)。
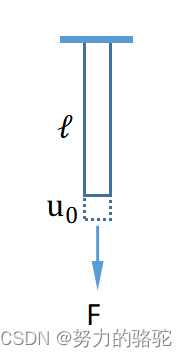
图1.2.1 一维杆拉伸变形示意图
W
=
∫
0
u
0
F
⋅
d
u
=
∫
0
ε
0
σ
A
⋅
d
ε
l
=
A
l
‾
↑
V
∫
0
ε
0
σ
d
ε
‾
↑
U
ε
(1-41)
W=\int_{0}^{u_{0}} F\cdot du= \int^{\varepsilon_{0}}_{0}\sigma A\cdot d\varepsilon l=\mathop{\underline {Al}}\limits_{\mathop{ \uparrow}\limits_{\mathop{ }\limits_{V}}}\mathop {\underline{\int^{\varepsilon_{0}}_{0}\sigma d\varepsilon}}\limits_{\mathop{ \uparrow}\limits_{U_{\varepsilon}}}\tag{1-41}
W=∫0u0F⋅du=∫0ε0σA⋅dεl=V↑AlUε↑∫0ε0σdε(1-41)
其中上式最后一项左侧两项乘积即为一维杆体积,右侧积分项即为单位体积储存的变形势能,即应变能密度。我们以典型的应力应变曲线为例,如下图。在应力应变曲线下方黄色区块面积为
σ
⋅
d
ε
\sigma\cdot \mathbf{d}\varepsilon
σ⋅dε,那么曲线下方的总面积为
∫
0
ε
0
σ
d
ε
\int^{\varepsilon_{0}}_{0}\sigma \mathbf{d}\varepsilon
∫0ε0σdε,因此应变能密度其实对应着应力应变曲线下方围成的面积。

图1.2.2 典型应力应变曲线
将一维的结果推广到三维,那么物体的应变能密度为
∫
0
ε
0
(
σ
11
d
ε
11
+
σ
22
d
ε
22
+
σ
33
d
ε
33
+
τ
12
d
γ
12
+
τ
13
d
γ
13
+
τ
23
d
γ
23
)
=
∫
0
ε
0
(
σ
11
d
ε
11
+
σ
22
d
ε
22
+
σ
33
d
ε
33
+
σ
12
d
ε
12
+
σ
21
d
ε
21
+
σ
13
d
ε
13
+
σ
31
d
ε
31
+
σ
23
d
ε
23
+
σ
32
d
ε
32
)
=
∫
0
ε
σ
i
j
d
ε
i
j
(1-42)
\begin{aligned} &\int^{\varepsilon_{0}}_{0}(\sigma_{11} \mathbf{d}\varepsilon_{11}+\sigma_{22} \mathbf{d}\varepsilon_{22}+\sigma_{33} \mathbf{d}\varepsilon_{33}+\tau_{12} \mathbf{d}\gamma_{12}+\tau_{13} \mathbf{d}\gamma_{13}+\tau_{23} \mathbf{d}\gamma_{23})\\ =&\int^{\varepsilon_{0}}_{0}(\sigma_{11} \mathbf{d}\varepsilon_{11}+\sigma_{22} \mathbf{d}\varepsilon_{22}+\sigma_{33} \mathbf{d}\varepsilon_{33}+\sigma_{12} \mathbf{d}\varepsilon_{12}+\sigma_{21} \mathbf{d}\varepsilon_{21}+\sigma_{13} \mathbf{d}\varepsilon_{13}+\sigma_{31} \mathbf{d}\varepsilon_{31}+\sigma_{23} \mathbf{d}\varepsilon_{23}+\sigma_{32} \mathbf{d}\varepsilon_{32})\\ =&\int^{\varepsilon}_{0}\sigma_{ij} \mathbf{d}\varepsilon_{ij}\end{aligned} \tag{1-42}
==∫0ε0(σ11dε11+σ22dε22+σ33dε33+τ12dγ12+τ13dγ13+τ23dγ23)∫0ε0(σ11dε11+σ22dε22+σ33dε33+σ12dε12+σ21dε21+σ13dε13+σ31dε31+σ23dε23+σ32dε32)∫0εσijdεij(1-42)
上式中应用了
σ
12
=
σ
21
=
τ
12
\sigma_{12}=\sigma_{21}=\tau_{12}
σ12=σ21=τ12,
ε
12
=
ε
21
=
1
2
γ
12
\varepsilon_{12}=\varepsilon_{21}=\frac{1}{2}\gamma_{12}
ε12=ε21=21γ12,
σ
13
=
σ
31
=
τ
13
\sigma_{13}=\sigma_{31}=\tau_{13}
σ13=σ31=τ13,
ε
13
=
ε
31
=
1
2
γ
13
\varepsilon_{13}=\varepsilon_{31}=\frac{1}{2}\gamma_{13}
ε13=ε31=21γ13,
σ
23
=
σ
32
=
τ
23
\sigma_{23}=\sigma_{32}=\tau_{23}
σ23=σ32=τ23,
ε
23
=
ε
32
=
1
2
γ
23
\varepsilon_{23}=\varepsilon_{32}=\frac{1}{2}\gamma_{23}
ε23=ε32=21γ23,同理,应变余能密度可以推导是
∫
0
ε
ε
i
j
d
σ
i
j
(1-43)
\int^{\varepsilon}_{0}\varepsilon_{ij} \mathbf{d}\sigma_{ij}\tag{1-43}
∫0εεijdσij(1-43)
1.2.1.c 最小势能原理变分基础
最小势能原理是一个物理学普遍性的原理,物质系统经过一系列的作用,最终达到的平衡状态一定是总体势能处于最小的状态。力学系统的最小势能原理可以表述为:力学系统所有的可能位移中,真实发生的位移,一定是使力学系统势能取到最小。
在线弹性力学中,物体从零应力状态变成平衡状态,其应力与应变按照下图变化(物体处于弹性变形,应力应变方程为线性关系)。

图1.2.3 应力应变关系示意图
那么物体的应变势能如下式所示。
U
=
∫
Ω
∫
ε
σ
i
j
d
ε
i
j
d
Ω
=
1
2
∫
Ω
σ
i
j
ε
i
j
d
Ω
(1-44)
U=\int_{\Omega}\int_{\varepsilon}\sigma_{ij} \mathbf{d}\varepsilon_{ij}\mathbf{d}\Omega=\frac{1}{2}\int_{\Omega}\sigma_{ij}\varepsilon_{ij}\mathbf{d}\Omega\tag{1-44}
U=∫Ω∫εσijdεijdΩ=21∫ΩσijεijdΩ(1-44)
物体的外力功分体力做的功和面力做的功,如下所示
d
W
f
=
f
i
⋅
u
i
=
b
i
d
Ω
⋅
u
i
(1-45)
dW_{f} =f_{i}\cdot u_{i}=b_{i}d\Omega \cdot u_{i}\tag{1-45}
dWf=fi⋅ui=bidΩ⋅ui(1-45)
其中
f
i
f_{i}
fi体积力,
b
i
d
Ω
b_{i}d\Omega
bidΩ为单位体积受到的体积力。
d
W
p
=
f
‾
i
⋅
u
i
=
p
i
d
A
⋅
u
i
(1-46)
dW_{p} =\overline f_{i}\cdot u_{i}=p_{i}dA \cdot u_{i}\tag{1-46}
dWp=fi⋅ui=pidA⋅ui(1-46)
其中
f
‾
i
\overline f_{i}
fi面力,
p
i
d
A
p_{i}dA
pidA为单位面积受到的面力。
总的外力功如下
W
=
∫
Ω
d
W
f
+
d
W
p
=
∫
Ω
b
i
u
i
d
Ω
+
∫
A
p
i
u
i
d
A
(1-47)
\begin{aligned} W &= \int_{\Omega}dW_{f} +dW_{p} \\ &=\int_{\Omega} b_{i}u_{i}d\Omega +\int_{A}p_{i}u_{i}dA\end{aligned} \tag{1-47}
W=∫ΩdWf+dWp=∫ΩbiuidΩ+∫ApiuidA(1-47)
那么物体的外力势能为
V
=
−
W
=
−
(
∫
Ω
d
W
f
+
d
W
p
)
=
−
∫
Ω
b
i
u
i
d
Ω
−
∫
A
p
i
u
i
d
A
(1-48)
\begin{aligned} V&=-W \\ &=-( \int_{\Omega}dW_{f} +dW_{p}) \\ &=-\int_{\Omega} b_{i}u_{i}d\Omega -\int_{A}p_{i}u_{i}dA \end{aligned} \tag{1-48}
V=−W=−(∫ΩdWf+dWp)=−∫ΩbiuidΩ−∫ApiuidA(1-48)
那么物体的总势能为
I
I
=
U
+
V
=
U
−
W
=
1
2
∫
Ω
σ
i
j
ε
i
j
d
Ω
−
∫
Ω
b
i
u
i
d
Ω
−
∫
A
p
i
u
i
d
A
=
1
2
∫
Ω
D
i
j
k
l
ε
i
j
ε
k
l
d
Ω
−
∫
Ω
b
i
u
i
d
Ω
−
∫
A
p
i
u
i
d
A
(1-49)
\begin{aligned} II &=U+V\\ &=U-W\\ &=\frac{1}{2}\int_{\Omega}\sigma_{ij}\varepsilon_{ij}d\Omega-\int_{\Omega} b_{i}u_{i}d\Omega -\int_{A}p_{i}u_{i}dA\\ &=\frac{1}{2}\int_{\Omega}D_{ijkl}\varepsilon_{ij}\varepsilon_{kl}d\Omega-\int_{\Omega} b_{i}u_{i}d\Omega -\int_{A}p_{i}u_{i}dA \end{aligned}\tag{1-49}
II=U+V=U−W=21∫ΩσijεijdΩ−∫ΩbiuidΩ−∫ApiuidA=21∫ΩDijklεijεkldΩ−∫ΩbiuidΩ−∫ApiuidA(1-49)
(下面内容不增加泛函的情况下提出变分)
最小势能原理的变分提法:在所有满足位移边界条件的可能位移中,真实会发生的位移,使得物体总势能取得最小值。本文我们不展开变分的概念(涉及泛函的概念),仅仅引入两个结论:(1)变分是微分的扩展(2)变分求导方法与微分求导一致。那么最小势能原理等同于函数最小值求解(精确的说是泛函的最小值求解),最小值求解的条件就是一阶导数为零,二阶导数大于零。同样原理,最小势能原理的求解条件为物体总势能的一阶变分为零,二阶变分大于零。即:
δ
I
I
=
∂
I
I
∂
ε
i
j
δ
ε
i
j
+
∂
I
I
∂
u
i
δ
u
i
=
∫
Ω
D
i
j
k
l
ε
i
j
δ
ε
k
l
d
Ω
−
∫
Ω
b
i
δ
u
i
d
Ω
−
∫
A
p
i
δ
u
i
d
A
=
∫
Ω
σ
k
l
δ
ε
k
l
d
Ω
−
∫
Ω
b
i
δ
u
i
d
Ω
−
∫
A
p
i
δ
u
i
d
A
=
∫
Ω
σ
i
j
δ
ε
i
j
d
Ω
−
∫
Ω
b
i
δ
u
i
d
Ω
−
∫
A
p
i
δ
u
i
d
A
(1-50)
\begin{aligned} \delta II &=\frac{\partial II}{\partial \varepsilon_{ij}}\delta\varepsilon_{ij}+\frac{\partial II}{\partial u_{i}}\delta u_{i}\\ &=\int_{\Omega}D_{ijkl}\varepsilon_{ij}\delta\varepsilon_{kl}d\Omega-\int_{\Omega} b_{i}\delta u_{i}d\Omega -\int_{A}p_{i}\delta u_{i}dA\\ &=\int_{\Omega}\sigma_{kl}\delta\varepsilon_{kl}d\Omega-\int_{\Omega} b_{i}\delta u_{i}d\Omega -\int_{A}p_{i}\delta u_{i}dA\\ &=\int_{\Omega}\sigma_{ij}\delta\varepsilon_{ij}d\Omega-\int_{\Omega} b_{i}\delta u_{i}d\Omega -\int_{A}p_{i}\delta u_{i}dA \end{aligned}\tag{1-50}
δII=∂εij∂IIδεij+∂ui∂IIδui=∫ΩDijklεijδεkldΩ−∫ΩbiδuidΩ−∫ApiδuidA=∫ΩσklδεkldΩ−∫ΩbiδuidΩ−∫ApiδuidA=∫ΩσijδεijdΩ−∫ΩbiδuidΩ−∫ApiδuidA(1-50)
在上式中将几何方程代入
∫
Ω
σ
i
j
δ
ε
i
j
d
Ω
=
∫
Ω
σ
i
j
⋅
1
2
δ
(
∂
u
i
∂
x
j
+
∂
u
j
∂
x
i
)
d
Ω
=
∫
Ω
1
2
σ
i
j
δ
(
∂
u
i
∂
x
j
)
+
1
2
σ
i
j
δ
(
∂
u
j
∂
x
i
)
d
Ω
=
∫
Ω
1
2
σ
i
j
δ
(
∂
u
i
∂
x
j
)
+
1
2
σ
j
i
δ
(
∂
u
i
∂
x
j
)
d
Ω
=
∫
Ω
σ
i
j
δ
(
∂
u
i
∂
x
j
)
d
Ω
=
∫
Ω
∂
∂
x
j
(
σ
i
j
δ
u
i
)
d
Ω
−
∫
Ω
∂
σ
i
j
∂
x
j
δ
u
i
d
Ω
(1-51)
\begin{aligned} \int_{\Omega}\sigma_{ij}\delta\varepsilon_{ij}d\Omega &=\int_{\Omega}\sigma_{ij}\cdot \frac{1}{2}\delta(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})d\Omega\\ &=\int_{\Omega}\frac{1}{2}\sigma_{ij}\delta(\frac{\partial u_i}{\partial x_j})+\frac{1}{2}\sigma_{ij}\delta(\frac{\partial u_j}{\partial x_i})d\Omega\\ &=\int_{\Omega}\frac{1}{2}\sigma_{ij}\delta(\frac{\partial u_i}{\partial x_j})+\frac{1}{2}\sigma_{ji}\delta(\frac{\partial u_i}{\partial x_j})d\Omega\\ &=\int_{\Omega}\sigma_{ij}\delta(\frac{\partial u_i}{\partial x_j})d\Omega\\ &=\int_{\Omega}\frac{\partial}{\partial x_{j}}(\sigma_{ij}\delta u_i)d\Omega-\int_{\Omega}\frac{\partial \sigma_{ij}}{\partial x_{j}}\delta u_id\Omega \end{aligned}\tag{1-51}
∫ΩσijδεijdΩ=∫Ωσij⋅21δ(∂xj∂ui+∂xi∂uj)dΩ=∫Ω21σijδ(∂xj∂ui)+21σijδ(∂xi∂uj)dΩ=∫Ω21σijδ(∂xj∂ui)+21σjiδ(∂xj∂ui)dΩ=∫Ωσijδ(∂xj∂ui)dΩ=∫Ω∂xj∂(σijδui)dΩ−∫Ω∂xj∂σijδuidΩ(1-51)
上式中应用
σ
i
j
=
σ
j
i
\sigma_{ij}=\sigma_{ji}
σij=σji,以及分部积分。上式中第一项
∫
Ω
∂
∂
x
j
(
σ
i
j
δ
u
i
)
d
Ω
\int_{\Omega}\frac{\partial}{\partial x_{j}}(\sigma_{ij}\delta u_i)d\Omega
∫Ω∂xj∂(σijδui)dΩ应用高斯积分变换,有
∫
Ω
∂
∂
x
j
(
σ
i
j
δ
u
i
)
d
Ω
=
∫
Ω
[
∂
∂
x
1
(
σ
i
1
δ
u
i
)
+
∂
∂
x
2
(
σ
i
2
δ
u
i
)
+
∂
∂
x
3
(
σ
i
3
δ
u
i
)
]
d
Ω
=
∫
A
[
(
σ
i
1
δ
u
i
)
⋅
n
1
+
(
σ
i
2
δ
u
i
)
⋅
n
2
+
(
σ
i
3
δ
u
i
)
⋅
n
3
]
d
A
=
∫
A
σ
i
j
δ
u
i
⋅
n
j
d
A
(1-52)
\begin{aligned} \int_{\Omega}\frac{\partial}{\partial x_{j}}(\sigma_{ij}\delta u_i)d\Omega &=\int_{\Omega}[\frac{\partial}{\partial x_1}(\sigma_{i1}\delta u_i)+\frac{\partial}{\partial x_2}(\sigma_{i2}\delta u_i)+\frac{\partial}{\partial x_3}(\sigma_{i3}\delta u_i)]d\Omega\\ & =\int_{A}[(\sigma_{i1}\delta u_i)\cdot n_1+(\sigma_{i2}\delta u_i)\cdot n_2+(\sigma_{i3}\delta u_i)\cdot n_3]dA\\ & =\int_{A}\sigma_{ij}\delta u_i\cdot n_jdA \end{aligned}\tag{1-52}
∫Ω∂xj∂(σijδui)dΩ=∫Ω[∂x1∂(σi1δui)+∂x2∂(σi2δui)+∂x3∂(σi3δui)]dΩ=∫A[(σi1δui)⋅n1+(σi2δui)⋅n2+(σi3δui)⋅n3]dA=∫Aσijδui⋅njdA(1-52)
其中
d
Ω
d\Omega
dΩ为空间三维微元体,
d
A
dA
dA是该空间三维微元体的整个外表面,
n
j
n_j
nj即为这些外表面的方向余弦。
将上式代入(1-51),有
δ
I
I
=
∫
Ω
σ
i
j
δ
ε
i
j
d
Ω
−
∫
Ω
b
i
δ
u
i
d
Ω
−
∫
A
p
i
δ
u
i
d
A
=
∫
A
σ
i
j
n
j
δ
u
i
d
A
−
∫
Ω
∂
σ
i
j
∂
x
j
δ
u
i
d
Ω
−
∫
Ω
b
i
δ
u
i
d
Ω
−
∫
A
p
i
δ
u
i
d
A
=
∫
A
(
σ
i
j
n
j
−
p
i
)
δ
u
i
d
A
−
∫
Ω
(
∂
σ
i
j
∂
x
j
+
b
i
)
δ
u
i
d
Ω
(1-53)
\begin{aligned} \delta II &=\int_{\Omega}\sigma_{ij}\delta\varepsilon_{ij}d\Omega-\int_{\Omega} b_{i}\delta u_{i}d\Omega -\int_{A}p_{i}\delta u_{i}dA\\ & =\int_{A}\sigma_{ij}n_j\delta u_i dA-\int_{\Omega}\frac{\partial \sigma_{ij}}{\partial x_{j}}\delta u_id\Omega-\int_{\Omega} b_{i}\delta u_{i}d\Omega -\int_{A}p_{i}\delta u_{i}dA\\ &=\int_{A}(\sigma_{ij}n_j-p_{i})\delta u_{i}dA-\int_{\Omega}(\frac{\partial \sigma_{ij}}{\partial x_{j}}+b_{i})\delta u_id\Omega \end{aligned}\tag{1-53}
δII=∫ΩσijδεijdΩ−∫ΩbiδuidΩ−∫ApiδuidA=∫AσijnjδuidA−∫Ω∂xj∂σijδuidΩ−∫ΩbiδuidΩ−∫ApiδuidA=∫A(σijnj−pi)δuidA−∫Ω(∂xj∂σij+bi)δuidΩ(1-53)
由变分的任意性,可得
σ
i
j
n
j
−
p
i
=
0
∂
σ
i
j
∂
x
j
+
b
i
=
0
(1-53)
\begin{aligned} \sigma_{ij}n_j-p_{i}=0\\ \frac{\partial \sigma_{ij}}{\partial x_{j}}+b_{i}=0 \end{aligned}\tag{1-53}
σijnj−pi=0∂xj∂σij+bi=0(1-53)
也就是说总是能够找到满足位移边界条件可能位移,在满足几何方程和本构方程的前提下,物体总势能取到最小就是真实位移,该位移导出的应力应变能够精确的满足平衡方程和力边界条件。