实现 函数 F01、F06 的优化测试
以下内容是现有算法的运行结果、调参分析、及代码实现,用于给其他人提供参考,懒得改了hh
1. 运行结果
-
参数
w = 0.5 (可更改)
c1 = 2.0 (可更改)
c2 = 2.0 (可更改)
swarmSize = 30 (可更改)
v_max = 5 (可更改)
v_min = -5 (可更改)
dimension = 2
iterations = 1000 (可更改) -
输出(因为粒子群算法有一定随机性,所以给出三组输出样例)
-
第一组
-
控制台

-
收敛图像
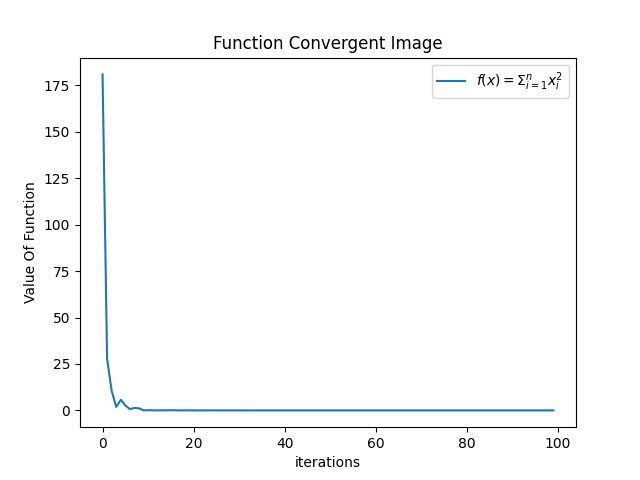
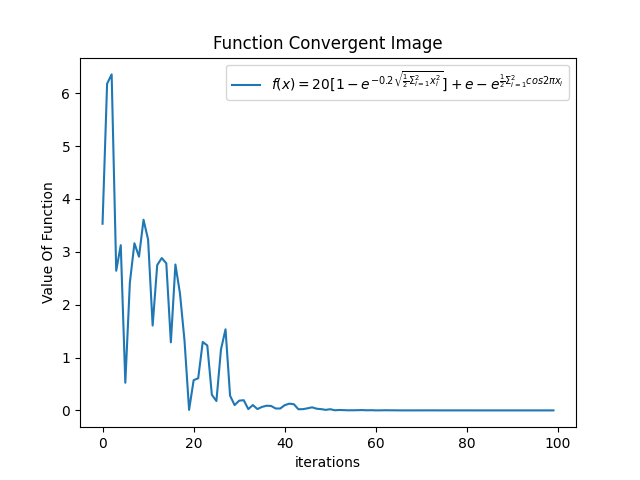
-
-
第二组

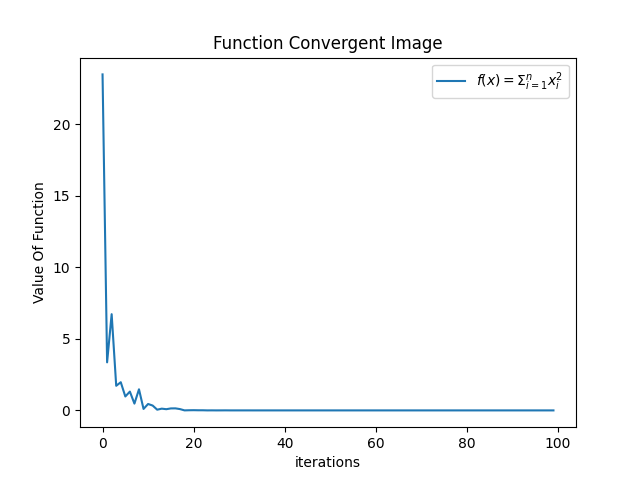
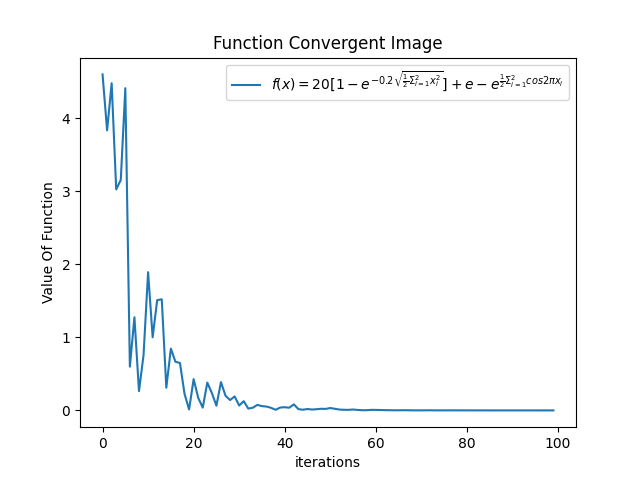
-
第三组

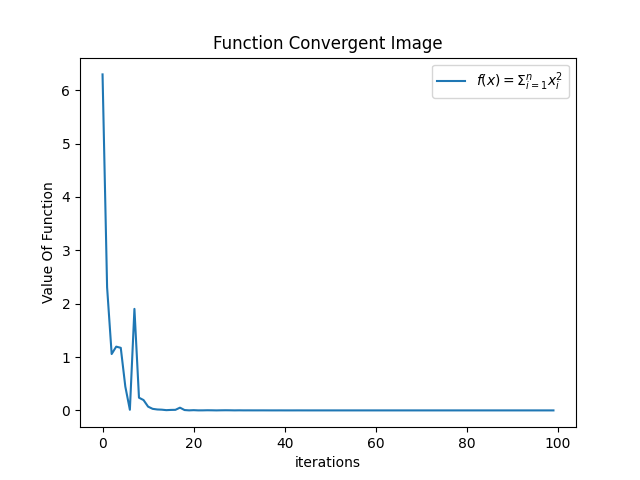
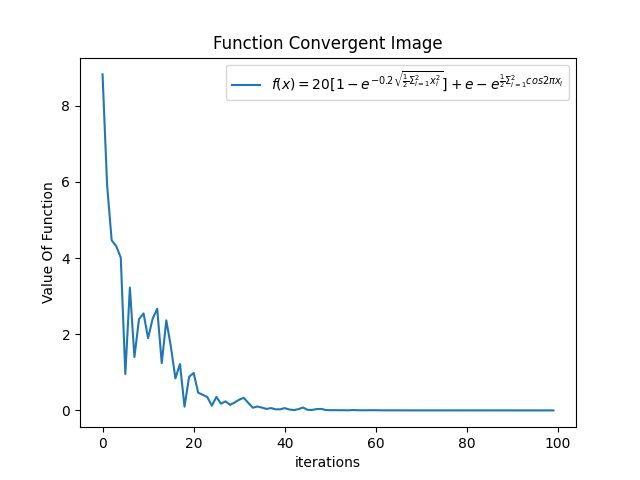
-
-
小结:根据上述输出我们知道,在上述参数的配置下,函数收敛情况不错,并且最终也得到了相当高精度的结果,即解向量特别趋近于 [0,0] 了
2. 调参分析
- 为什么要调参?粒子群算法的核心是个体位置和速度的更新,而个体位置和速度的更新取决于其自身因素(自身速度),社会因素(粒子群最佳位置),认知因素(历史最佳位置)决定,因此每一个因素的变化都会导致算法收敛程度的改变
- 调参——自身因素,因为自身因素包括惯性权重和原本速度两个方面,因此我们可以对惯性权重和速度范围进行调整,并观察结果
-
在其他参数不变的情况下,w = 0.9,我们发现函数收敛情况变得不好了

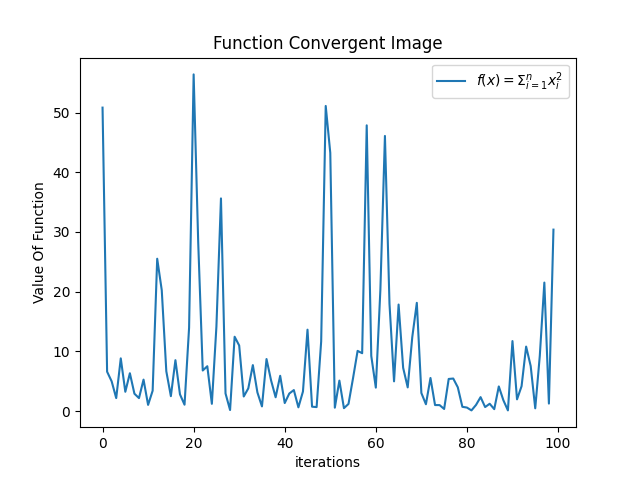
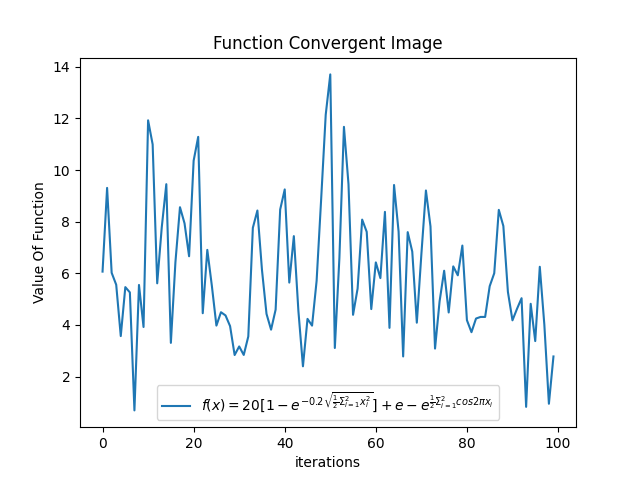
-
w = 0.1,我们发现,函数收敛情况变好了

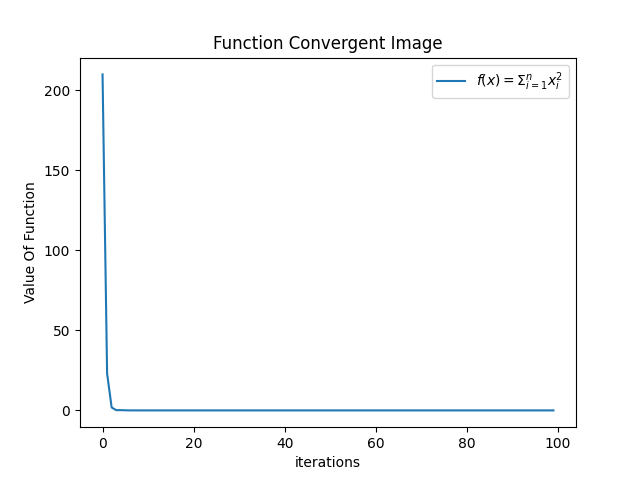
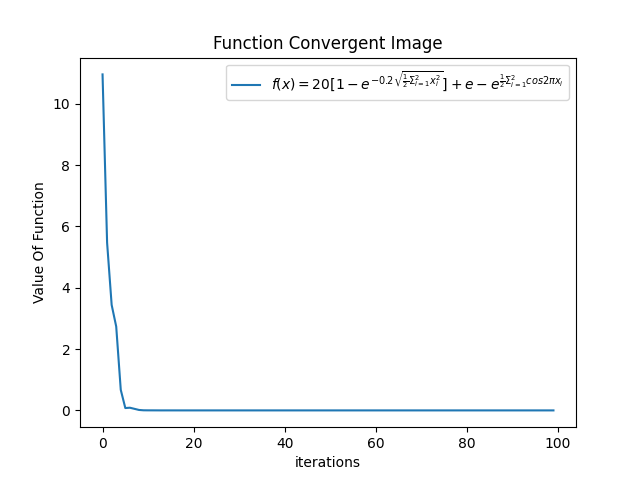
-
小结:惯性权重减少,使得粒子探索空间的能力减弱,但是收敛的精度大大提高。因为这里测试的两个函数是单峰函数,因此不需要考虑因为w过小导致粒子群陷入局部优化的问题,因此可以推导,对于单峰函数的优化,w 取小一点效果会更好。另外,更改 v_min\v_max 一定程度上也是更改粒子群的搜索空间的广度,与更改 w 具有类似的作用,故而不进行调参测试
-
- 调参——社会因素&认知因素
- 在其他参数不变的情况下,c1 = 1.0,c2=3.0,即社会因素更强,相比于初始情况,没有过大变化

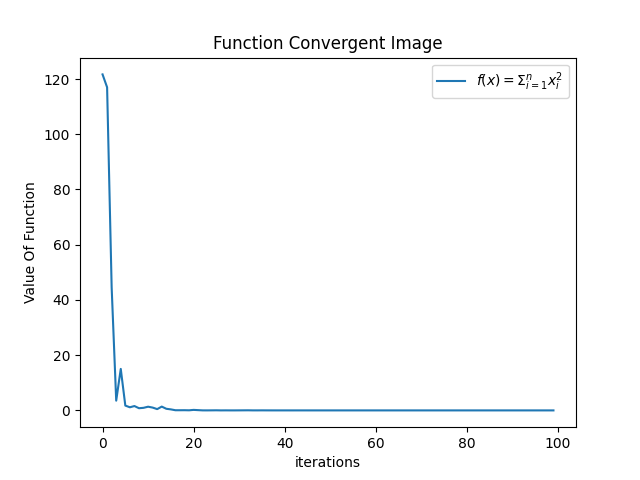
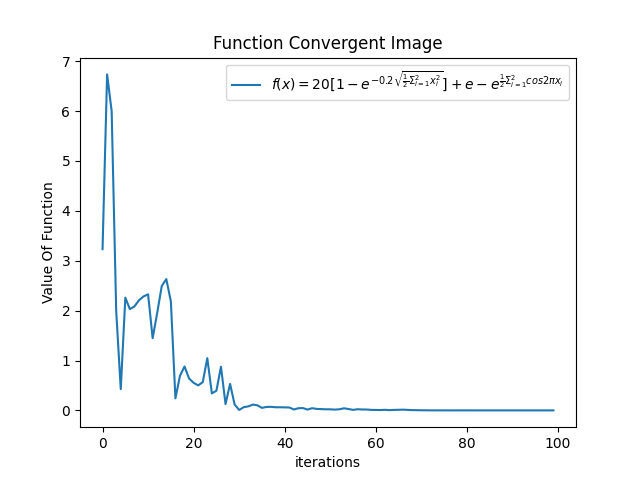
- c1 = 3.5, c2 = 0.5,显然,F06 收敛效果变好,即当粒子的运动更多关注自身历史最佳位置时,其搜索效果可能会改变

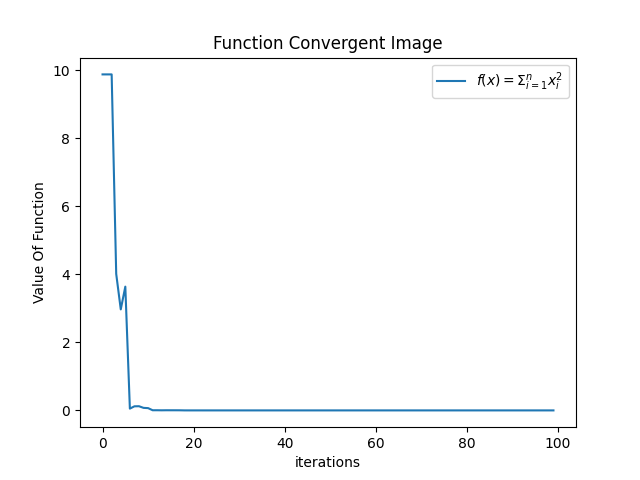
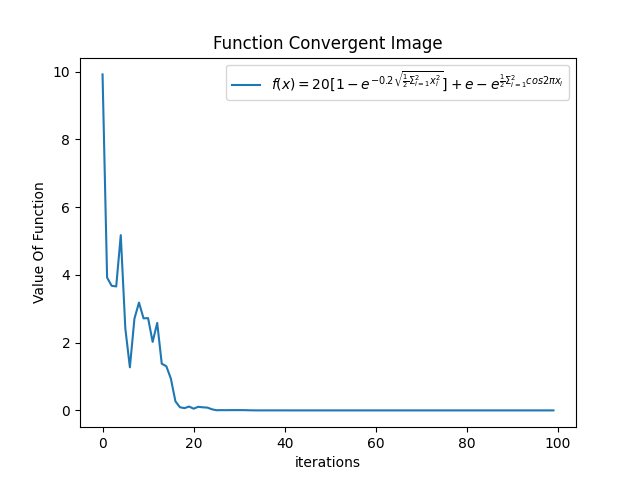
- 在其他参数不变的情况下,c1 = 1.0,c2=3.0,即社会因素更强,相比于初始情况,没有过大变化
3. 代码实现
import random
import math
from matplotlib import pyplot as plt
w = 0.5 # 惯性权重,①取值大有利于全局搜索,不利于局部搜索,②取值小有利于局部搜索,不利于全局搜索,容易陷入“局部最优”
c1 = 2.0 # “认知部分” 的加速因子
c2 = 2.0 # “社会部分” 的加速因子
swarmSize = 30 # 粒子规模
v_max = 5 # 粒子最大速度
v_min = -5 # 粒子的最小速度
dimension = 2 # 搜索空间的维度,也是位置向量和速度向量的维度,也是粒子的维度
iterations = 100 # 收敛次数/迭代次数
class Particle:
""" 粒子群中粒子的定义 """
def __init__(self, domain):
""" 粒子初始化 """
self.velocity = [] # 速度向量
self.pos = [] # 位置向量
self.pBest = [] # 最佳位置
self.domain = domain # 二维向量,表示粒子位置向量每个维度变量的取值范围(这里规定粒子每个维度的变量的取值范围相同)
for i in range(dimension):
self.pos.append((domain[1] - domain[0]) *
random.random() + domain[0]) # 初始化粒子的位置向量,随机数范围在 [下限,上限)
self.velocity.append(0.01 * random.random() +
v_min) # 初始化粒子的速度向量,随机数范围在 [v_min,v_max)
self.pBest.append(self.pos[i]) # 初始化粒子的历史最佳位置向量,初始时刻即当前位置
return
def updateVelocity(self, gBest):
""" 更新速度向量 """
''' gBest 表示当前粒子群的最优位置,需要作参数传入 '''
for i in range(dimension):
r1 = random.random()
r2 = random.random()
cognitive = c1 * r1 * (self.pBest[i] - self.pos[i]) # 认知部分的分量
social = c2 * r2 * (gBest[i] - self.pos[i]) # 社会部分的分量
self.velocity[i] = w * self.velocity[i] + \
cognitive + social # 更新速度向量
return
def updatePosition(self):
""" 更新位置向量 """
for i in range(dimension):
self.pos[i] = self.pos[i] + self.velocity[i]
return
def satisfyConstraints(self):
""" 让当前粒子的位置向量和速度向量满足限制条件 """
for i in range(dimension):
x = self.pos[i] # 满足位置向量的限制条件,即应该在其取值范围之间
if x > self.domain[1]:
self.pos[i] = self.domain[1]
elif x < self.domain[0]:
self.pos[i] = self.domain[0]
v = self.velocity[i] # 更新速度向量的限制条件,即应该在 [v_min, v_max] 范围内
if v > v_max:
self.velocity[i] = v_max
elif v < v_min:
self.velocity[i] = v_min
return
class ParticleSwarmOptimizer:
""" POS 优化器的定义 """
def __init__(self, optimizeFun):
""" 优化器的初始化:即初始化一个粒子种群 """
self.swarm = [] # 粒子群
self.gBest = [] # 粒子群的最佳位置
self.visual_y = [] # 作图纵坐标,用于记录每次迭代粒子群最佳位置的函数值
self.visual_x = [] # 作图横坐标,用于记录迭代次数
self.optimizeFun = optimizeFun # 函数类的实例对象
for i in range(swarmSize):
particle = Particle(self.optimizeFun.domain)
self.swarm.append(particle) # 初始化一个粒子种群
self.gBest = self.swarm[0].pBest # 获取粒子群初始状态的最佳位置
for i in range(swarmSize):
pBest = self.swarm[i].pBest
if self.f(pBest) > self.f(self.gBest): # 在我们看来,适应度
self.gBest = pBest
return
def optimize(self):
""" 优化函数 """
for i in range(iterations):
''' STEP 1 更新每个粒子的速度向量、位置向量 '''
for k in range(swarmSize):
self.swarm[k].updateVelocity(self.gBest)
self.swarm[k].updatePosition()
self.swarm[k].satisfyConstraints()
''' STEP 2 更新每个粒子的历史最佳位置 '''
for l in range(swarmSize):
if self.f(self.swarm[l].pos) > self.f(self.swarm[l].pBest):
self.swarm[l].pBest = self.swarm[l].pos
''' STEP 3 找到全局最佳值 '''
for j in range(swarmSize):
pBest = self.swarm[j].pBest
if self.f(pBest) > self.f(self.gBest): # 将每个粒子的最佳位置和粒子群最佳位置比较,从而获得最好的位置
self.gBest = pBest
self.visual_x.append(i)
self.visual_y.append(self.optimizeFun.fun(self.gBest[0], self.gBest[1]))
return self.gBest
def f(self, solution):
""" 计算 solution 的函数值,因为我们用于查找最小值,所以函数值取负值就是适应值 """
return -self.optimizeFun.fun(solution[0], solution[1])
def visualize(self):
plt.title("Function Convergent Image") # 图片标题
plt.xlabel("iterations") # x 轴变量名称
plt.ylabel("Value Of Function") # y 轴变量名称
plt.plot(self.visual_x, self.visual_y, label=self.optimizeFun.funName) # 逐点画图
plt.legend() # 画出曲线图标
plt.show() # 画出图像
class OptimizeFunctions:
""" 函数类,其中存储了待优化的函数及其变量的取值范围(我们假定函数自变量每个维度的取值范围相同) """
def __init__(self, key):
""" 根据传入的 key 初始化 domain 和 fun """
if key == 1:
self.domain = self.__domain_01 # 存储变量的取值范围
self.fun = self.__f01 # 存储用于优化的函数
self.funName = r"$f(x)=\Sigma_{i=1}^nx_i^2$" # 特定格式的函数表达式字符串
elif key == 6:
self.domain = self.__domain_06
self.fun = self.__f06
self.funName = r"$f(x)=20[1-e^{-0.2\sqrt{\frac{1}{2}\Sigma_{i=1}^2x_i^2}}]+e-e^{\frac{1}{2}\Sigma_{i=1}^2cos2\pi x_i}$"
__domain_01 = [-100, 100]
__domain_06 = [-32, 32]
def __f01(self, x1, x2):
return x1 * x1 + x2 * x2
def __f06(self, x1, x2):
return 20 * (1 - math.exp(-0.2 * math.sqrt(0.5 * (x1 * x1 + x2 * x2)))) + math.exp(1) - math.exp(
0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
def main():
optimizeFun = OptimizeFunctions(1)
optimizer = ParticleSwarmOptimizer(optimizeFun)
x = optimizer.optimize()
optimizer.visualize()
print("函数 01 优化得到最小值位置为", x)
optimizeFun = OptimizeFunctions(6)
optimizer = ParticleSwarmOptimizer(optimizeFun)
x = optimizer.optimize()
optimizer.visualize()
print("函数 06 优化得到最小值位置为", x)
if __name__ == '__main__':
main()