欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
文章字体风格：
红色文字表示：重难点
蓝色文字表示：思路以及想法
　
如果大家觉得有帮助的话，感谢大家帮忙点赞！收藏！转发！

法一： x，x+n，x+n+n

思路：

1. 因为有三种物种，A吃B，B吃C，C吃A
2. 如果我们用一个数组存储，那么比如1吃2，那么我们让2的角标处的值标记成1，如果3吃2，那怎么标记？一个数组指定标记不过来。
3. 那么我们想用三个数组存储，其实也存储不过来，因为角标就那么几个，
4. 最好的方法就是，用x，x+n，x+n+n来表示
   比如1吃2，那么就可能有三种情况，
   A类中的1吃B类的2 : fa[1] = fa[2+n+n]
   B类中的1吃C类的2 : fa[1+n] = fa[2]
   C类中的1中A类的2 : fa[1+n+n] = fa[2+n];
   这样的话，就会有3*n个角标，就可以充分表达
   A中的1吃B中的2（B中的2用2+n表示）
   这样的话就不会出现数字冲突

/*

*/

#include <bits/stdc++.h>
using namespace std;
int fa[200000];
int n,m,k,x,y,ans;
int get(int x)
{
    if(x==fa[x]) 
        return x;
    return fa[x]=get(fa[x]);
}
void merge(int x,int y)
{
    fa[get(x)]=get(y);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=3*n;i++) 
        fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&k,&x,&y);
        if(x>n || y>n) 
            ans++;
        else if(k==1)
        {
            if(get(x)==get(y+n) || get(x)==get(y+n+n)) //如果x,y是同类,但是x是y的捕食中的动物,或者x是y天敌中的动物,那么错误.
                ans++;
            else
            {
                merge(x,y);
                merge(x+n,y+n);
                merge(x+n+n,y+n+n);
            }
        }
        else
        {
            if(x==y || get(x)==get(y) || get(x)==get(y+n)) //x就是y,或者他们是同类,再或者是y的同类中有x
                ans++;//都是假话
            else
            {
                merge(x,y+n+n);//y的捕食域加入x
                merge(x+n,y);//x的天敌域加入y
                merge(x+n+n,y+n);//x的捕食域是y的同类域.
            }
        }
    }
    cout<<ans<<endl;
}

法二：将有关系的都存储在一个部落，用到根节点的距离表示关系

注意：

1. 原始距离都为0

2. find具有路径压缩的作用：子节点到根节点的距离 = 子节点到父节点的距离 + 父节点到根节点的距离

3. A吃B则 A的父节点 等于B的父节点

1. 具体步骤如图：

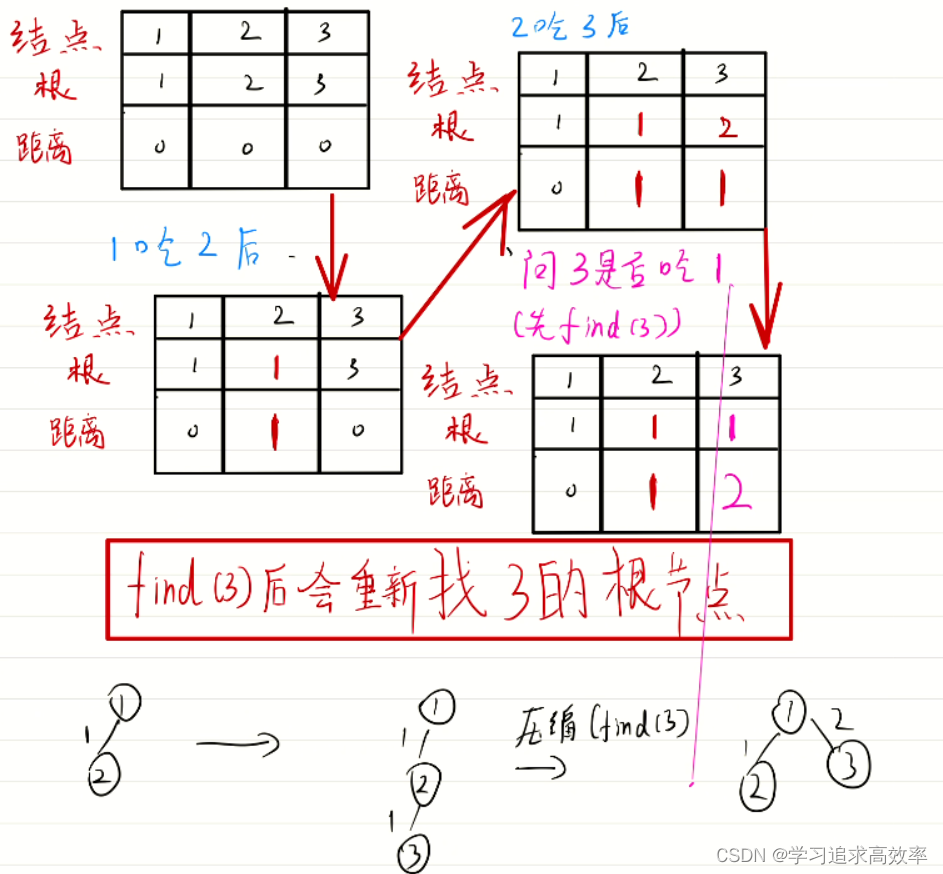
2. 为什么有路径压缩

3. 怎么处理两个根节点的距离（设数法）；距离可能是负数

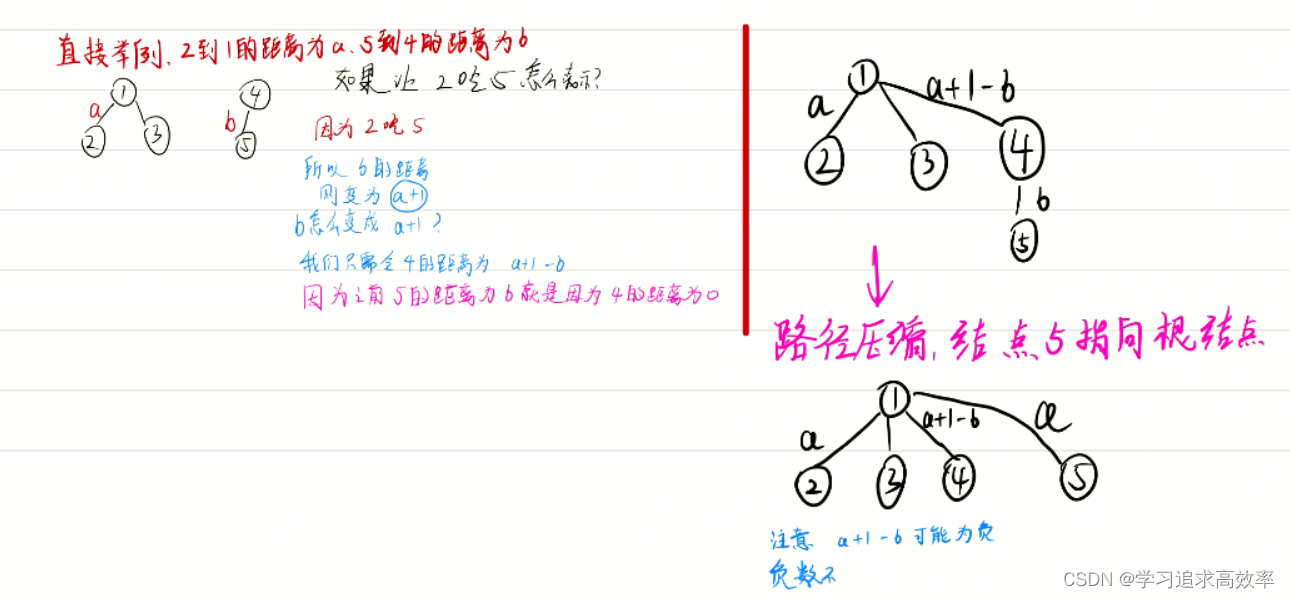
具体过程如下：

#include <iostream>

using namespace std;

const int N = 50010;

int n, m;
int p[N], d[N];

int find(int x)
{
    if (p[x] != x)
    {
        int t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;

    int res = 0;
    while (m -- )
    {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);

        if (x > n || y > n) res ++ ;
        else
        {
            int px = find(x), py = find(y);
            if (t == 1)
            {
                if (px == py && (d[x] - d[y]) % 3) res ++ ;
                else if (px != py)
                {
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }
            else
            {
                if (px == py && (d[x] - d[y] - 1) % 3) res ++ ;
                else if (px != py)
                {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }

    printf("%d\n", res);

    return 0;
}