树论(树形结构、二叉树、二叉搜索树、红黑树、Btree、B+Tree、赫夫曼树、堆树)
树形结构概念
在树形结构里面重要的术语:
-
结点:树里面的元素。
-
父子关系:结点之间相连的边
-
子树:当结点大于1时,其余的结点分为的互不相交的集合称为子树
-
度:一个结点拥有的子树数量称为结点的度
-
叶子:度为0的结点
-
孩子:结点的子树的根称为孩子结点
-
双亲:和孩子结点对应
-
兄弟:同一个双亲结点
-
森林:由N个互不相交的树构成深林
-
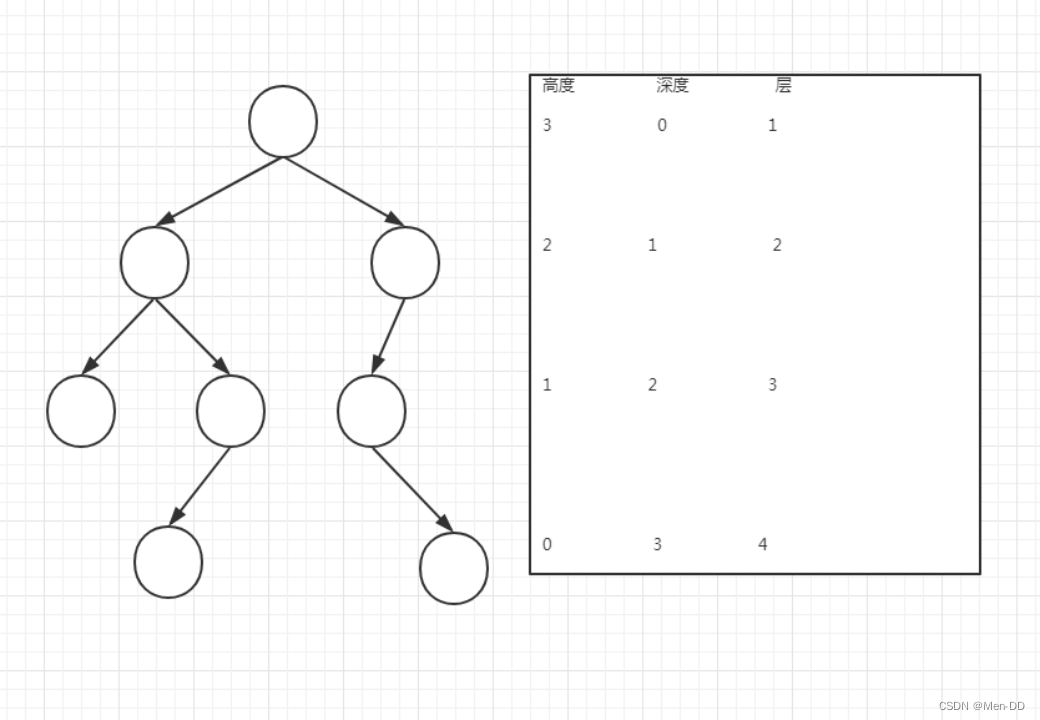
结点的高度:结点到叶子结点的最长路径
-
结点的深度:根结点到该结点的边个数
-
结点的层数:结点的深度加1
-
树的高度:根结点的高度
二叉树
Binary Tree: 一种特殊的树形结构,每个节点至多只有两颗子树
在二叉树的第N层上至多有2^(N-1)个结点。最多有2^N-1个结点个数。
分类:
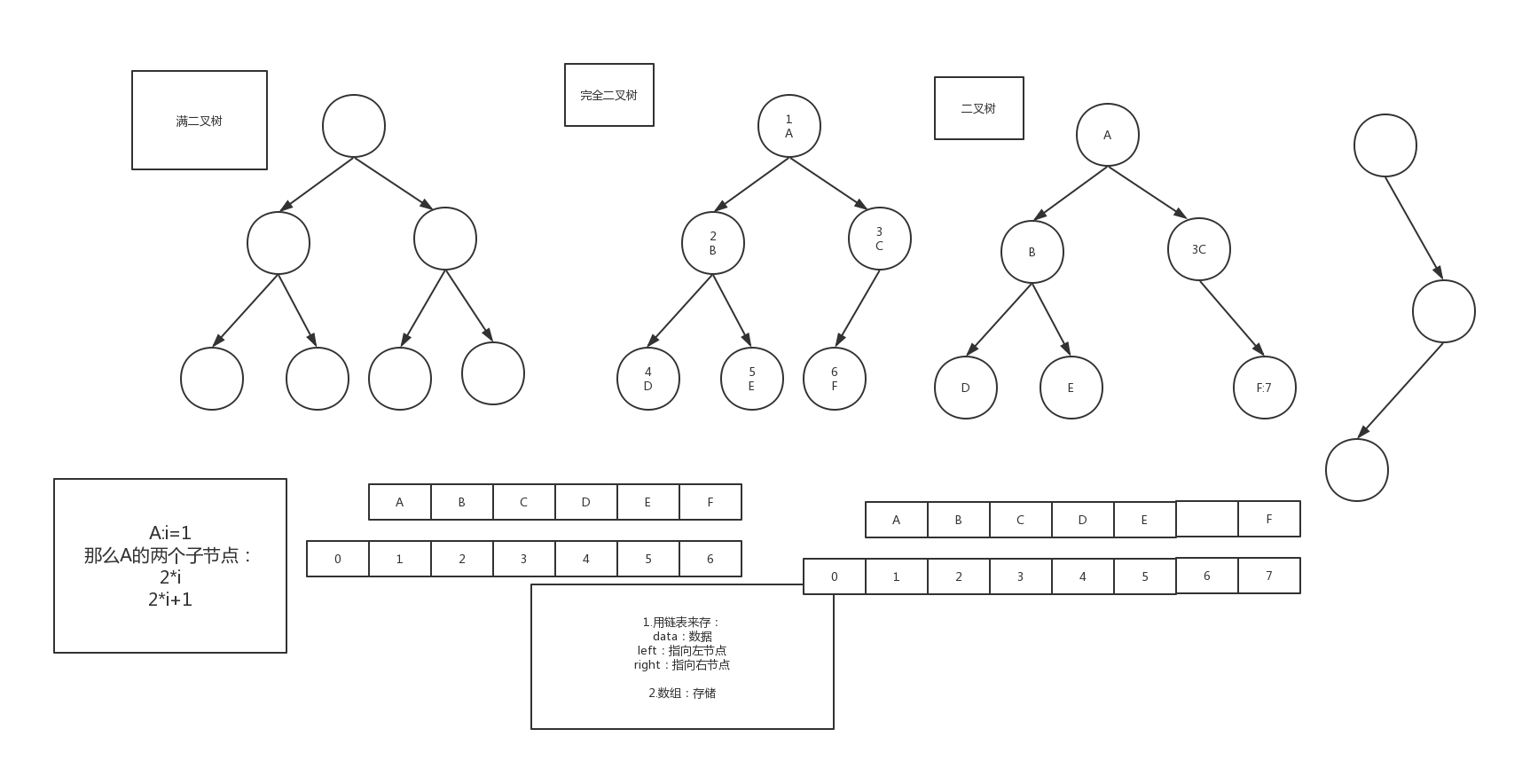
- 满二叉树:除叶子结点外,每个结点都有左右两个子结点。
- 完全二叉树:除最后一层外,其他的结点个数必须达到最大,并且最后一层结点都连续靠左排列。
思考
为什么要分满二叉树和完全二叉树呢?因为通过定义可以看出,完全二叉树只是满二叉树里面的一个子集
数组:性能高效,如果不是完全二叉树浪费空间
链表:也可以实现,性能没有数组高
二叉树遍历
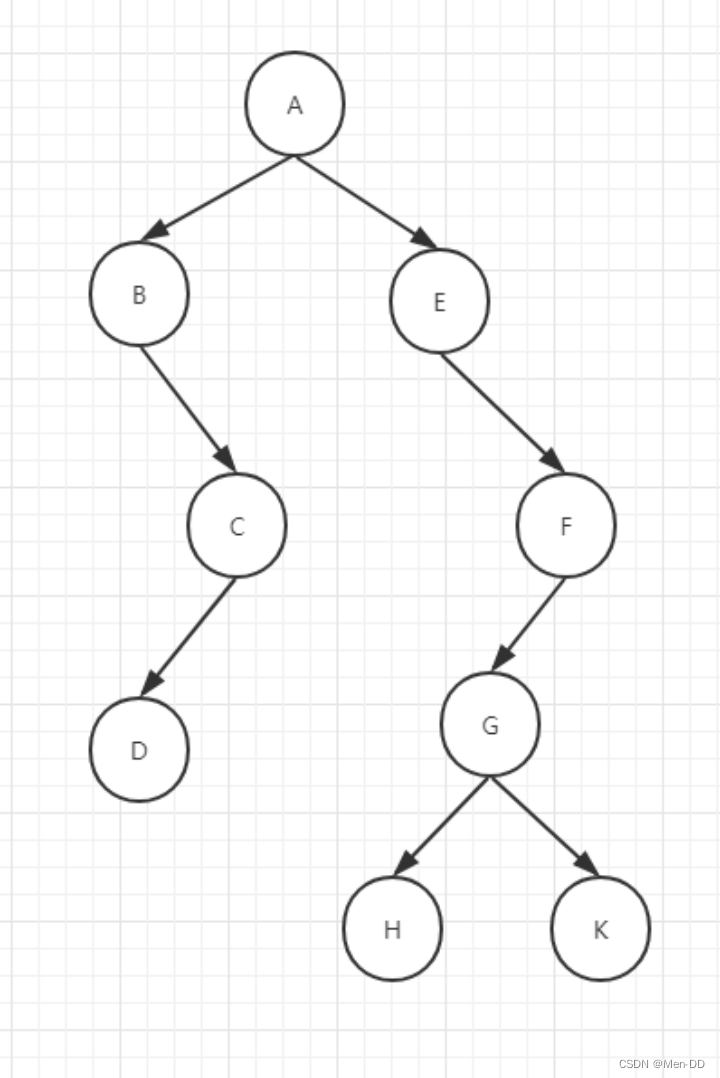
- 重要口诀:根节点输出!子树
- 前序:根 左 右 (A B C D E F G H K)
- 中序:左 根 右 (B C D A E F G H K)
- 后序:左 右 根 (B C D E F G H K A)
/**
* 二叉树--前中后链式遍历
* 前: A B C D E F G H K
* 中: B C D A E F G H K
* 后: B C D E F G H K A
* 层:
* A
* B E
* C F
* D G
* H K
*/
@Data
class TreeNode {
private char data;
private TreeNode left;
private TreeNode right;
public TreeNode(char data, TreeNode left, TreeNode right) {
this.data = data;
this.left = left;
this.right = right;
}
}
public class BinaryTree {
public void print(TreeNode node) {
System.out.print(node.getData() + " ");
}
public void pre(TreeNode root) { //前序:根(输出) 左 右 A B C D E F G H K
print(root);
if (root.getLeft() != null) {
pre(root.getLeft()); //认为是子树,分解子问题
}
if (root.getRight() != null) {
pre(root.getRight());
}
}
public void in(TreeNode root) { //中序:左 根(输出) 右 B C D A E F G H K
if (root.getLeft() != null) {
pre(root.getLeft()); //认为是子树,分解子问题
}
print(root);
if (root.getRight() != null) {
pre(root.getRight());
}
}
public void post(TreeNode root) { //后序:左 右 根(输出) B C D E F G H K A
if (root.getLeft() != null) {
pre(root.getLeft()); //认为是子树,分解子问题
}
if (root.getRight() != null) {
pre(root.getRight());
}
print(root);
}
public List<List<Character>> level(TreeNode root) { //层次遍历
if (root == null) return Collections.EMPTY_LIST;
List<List<Character>> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
List<Character> raw = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode item = queue.poll();
raw.add(item.getData());
if (item.getLeft() != null) {
queue.add(item.getLeft());
}
if (item.getRight() != null) {
queue.add(item.getRight());
}
}
res.add(raw);
}
return res;
}
public static void main(String[] args) {
TreeNode D = new TreeNode('D', null,null);
TreeNode H = new TreeNode('H', null,null);
TreeNode K = new TreeNode('K', null,null);
TreeNode C = new TreeNode('C', D,null);
TreeNode G = new TreeNode('G', H,K);
TreeNode B = new TreeNode('B', null,C);
TreeNode F = new TreeNode('F', G,null);
TreeNode E = new TreeNode('E', F,null);
TreeNode A = new TreeNode('A', B,E);
BinaryTree tree = new BinaryTree();
System.out.print("前: ");
tree.pre(A);
System.out.println();
System.out.print("中: ");
tree.in(A);
System.out.println();
System.out.print("后: ");
tree.post(A);
System.out.println();
System.out.println("层: ");
List<List<Character>> res = tree.level(A);
for (List<Character> re : res) {
for (Character character : re) {
System.out.print(character + " ");
}
System.out.println();
}
}
}
二叉搜索树(二叉查找树、二叉排序数)
- 如果它的左子树不为空,则左子树上结点的值都小于根结点
- 如果它的右子树不为空,则右子树上结点的值都大于根结点
- 子树同样也要遵循以上两点
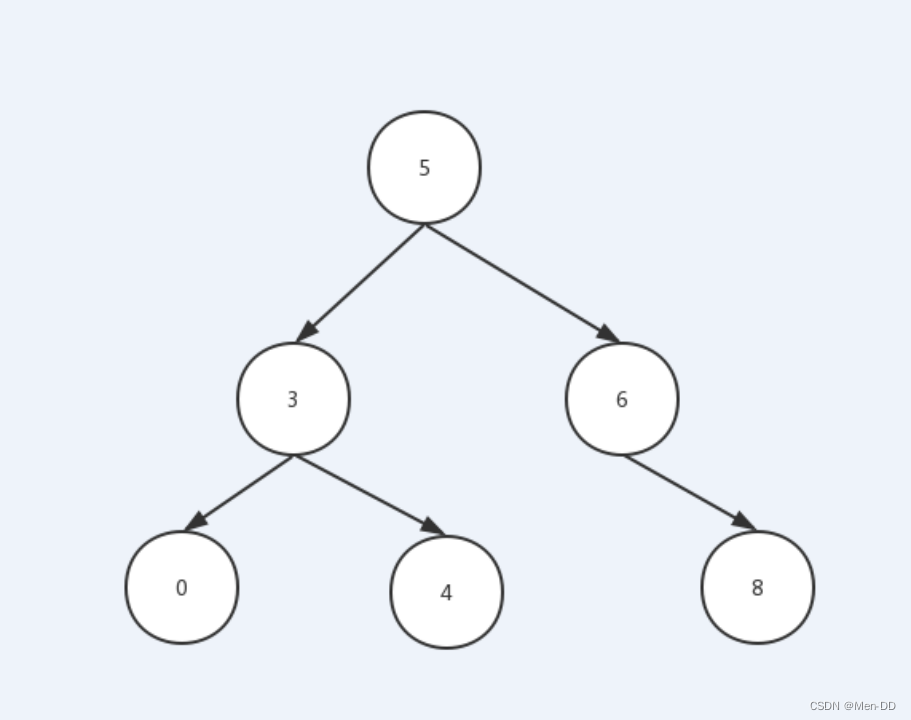
中序遍历 ---- 左 根(输出) 右:0 3 4 5 6 8
性能分析
- 查找logn
- 插入nlogn
- 删除
-
- 要删除的结点是叶子结点 O(1)
-
- 要删除的结点只有一个子树(左或者右)O(1)
-
- 要删除的结点有两颗子树:找后继结点,而且后继结点的左子树一定为空 logn
-
/**
* 二叉搜索树 增删改查
*/
class BinaryNodeTeacher {
int data;
BinaryNodeTeacher left;
BinaryNodeTeacher right;
BinaryNodeTeacher parent;
public BinaryNodeTeacher(int data) {
this.data = data;
this.left = null;
this.right = null;
this.parent = null;
}
}
public class BinarySearchTreeTeacher {
public BinaryNodeTeacher find(BinaryNodeTeacher root, int key) {
BinaryNodeTeacher current = root;
while (current != null) {
if (key < current.data) {
current = current.left;
} else if (key > current.data) {
current = current.right;
} else {
return current;
}
}
return null;
}
public void insert(BinaryNodeTeacher root, int data) {
if (root.data < data) {
if (root.right != null) {
insert(root.right, data);
} else {
BinaryNodeTeacher newNode = new BinaryNodeTeacher(data);
newNode.parent = root;
root.right = newNode;
}
} else {
if (root.left != null) {
insert(root.left, data);
} else {
BinaryNodeTeacher newNode = new BinaryNodeTeacher(data);
newNode.parent = root;
root.left = newNode;
}
}
}
public BinaryNodeTeacher finSuccessor(BinaryNodeTeacher node) { // 查找node的后继节点
if (node.right == null) { // 表示没有右边 那就没有后继
return node;
}
BinaryNodeTeacher cur = node.right;
BinaryNodeTeacher pre = node.right; // 开一个额外的空间 用来返回后继节点,因为我们要找到为空的时候,那么其实返回的是上一个节点
while (cur != null) {
pre = cur;
cur = cur.left; // 注意后继节点是要往左边找,因为右边的肯定比左边的大,我们要找的是第一个比根节点小的,所以只能往左边
}
return pre; // 因为cur会变成null,实际我们是要cur的上一个点,所以就是pre来代替
}
public BinaryNodeTeacher remove(BinaryNodeTeacher root, int data) { // 删除data
BinaryNodeTeacher delNode = find(root, data);
if (delNode == null) {
System.out.println("要删除的值不在树中");
return root;
}
// 1.删除的点没有左右子树
if (delNode.left == null && delNode.right == null) {
if (delNode == root) {
root = null;
} else if (delNode.parent.data < delNode.data) { // 说明删除的点是右子节点
delNode.parent.right = null;
} else {
delNode.parent.left = null;
}
} else if (delNode.left != null && delNode.right != null) { // 2.删除的节点有两颗子节点
BinaryNodeTeacher successor = finSuccessor(delNode); // 先找的后继节点
// 后继节点和删除节点进行交换,首先后继节点的左节点是肯定为空的
successor.left = delNode.left; // 后继的左边变为删除的左边
successor.left.parent = successor; // 删除点的左边parent指向后继节点
// 再来看后继节点的右边
if (successor.right != null && successor.parent != delNode) { // 后继节点有右边,这其实就是下面情况3的第一种
successor.right.parent = successor.parent;
successor.parent.left = successor.right;
successor.right = delNode.right;
successor.right.parent = successor;
}else if(successor.right == null) { //如果后继节点没有右边,那其实就是情况1,没有左右子树
if(successor.parent != delNode) { //如果后继节点的parent不等于删除的点 那么就需要把删除的右子树赋值给后继节点
successor.parent.left = null; //注意原来的后继节点上的引用要删掉,否则会死循环
successor.right = delNode.right;
successor.right.parent = successor;
}
}
// 替换做完接下来就要删除节点了
if (delNode == root) {
successor.parent = null;
root = successor;
return root;
}
successor.parent = delNode.parent;
if (delNode.data > delNode.parent.data) { // 删除的点在右边,关联右子树
delNode.parent.right = successor;
} else {
delNode.parent.left = successor;
}
} else { // 3.删除点有一个节点
if (delNode.right != null) { // 有右节点
if (delNode == root) {
root = delNode.right;
return root;
}
delNode.right.parent = delNode.parent; // 把右节点的parent指向删除点的parent
// 关联父节点的左右子树
if (delNode.data < delNode.parent.data) { // 删除的点在左边
delNode.parent.left = delNode.right;
} else {
delNode.parent.right = delNode.right;
}
} else {
if (delNode == root) {
root = delNode.left;
return root;
}
delNode.left.parent = delNode.parent;
if (delNode.data < delNode.parent.data) {
delNode.parent.left = delNode.left;
} else {
delNode.parent.right = delNode.left;
}
}
}
return root;
}
public void inOrde(BinaryNodeTeacher root) {
if (root != null) {
inOrde(root.left);
System.out.print(root.data);
inOrde(root.right);
}
}
// 用于获得树的层数
public int getTreeDepth(BinaryNodeTeacher root) {
return root == null ? 0 : (1 + Math.max(getTreeDepth(root.left), getTreeDepth(root.right)));
}
/**
*
* 测试用例
* 15
* 10
* 19
* 8
* 13
* 16
* 28
* 5
* 9
* 12
* 14
* 20
* 30
* -1
* 删除:15 8 5 10 12 19 16 14 30 9 13 20 28
*
* 15
* / \
* 10 19
* / \ / \
* 8 13 16 28
* / \ / \ / \
* 5 9 12 14 20 30
*/
public static void main(String[] args) {
BinarySearchTreeTeacher binarySearchTree = new BinarySearchTreeTeacher();
BinaryNodeTeacher root = null;
Scanner cin = new Scanner(System.in);
int t = 1;
System.out.println("二叉搜索树假定不存重复的子节点,重复可用链表处理,请注意~~");
System.out.println("请输入根节点:");
int rootData = cin.nextInt();
root = new BinaryNodeTeacher(rootData);
System.out.println("请输入第" + t + "个点:输入-1表示结束");
while (true) { //
int data = cin.nextInt();
if (data == -1)
break;
binarySearchTree.insert(root, data);
t++;
System.out.println("请输入第" + t + "个点:输入-1表示结束");
}
binarySearchTree.show(root); //找的别人写的打印二叉树形结构,感觉还不错,可以更加清晰
System.out.println("删除测试:");
while(true) {
System.out.println("请输入要删除的点:-1表示结束");
int key = cin.nextInt();
root = binarySearchTree.remove(root, key);
binarySearchTree.show(root);
if(root == null) {
System.out.println("树已经没有数据了~~");
break;
}
}
}
private void writeArray(BinaryNodeTeacher currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
// 保证输入的树不为空
if (currNode == null)
return;
// 先将当前节点保存到二维数组中
res[rowIndex][columnIndex] = String.valueOf(currNode.data);
// 计算当前位于树的第几层
int currLevel = ((rowIndex + 1) / 2);
// 若到了最后一层,则返回
if (currLevel == treeDepth)
return;
// 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔)
int gap = treeDepth - currLevel - 1;
// 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值
if (currNode.left != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.left, rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
// 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值
if (currNode.right != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.right, rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public void show(BinaryNodeTeacher root) {
if (root == null) {
System.out.println("EMPTY!");
return ;
}
// 得到树的深度
int treeDepth = getTreeDepth(root);
// 最后一行的宽度为2的(n - 1)次方乘3,再加1
// 作为整个二维数组的宽度
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
// 用一个字符串数组来存储每个位置应显示的元素
String[][] res = new String[arrayHeight][arrayWidth];
// 对数组进行初始化,默认为一个空格
for (int i = 0; i < arrayHeight; i++) {
for (int j = 0; j < arrayWidth; j++) {
res[i][j] = " ";
}
}
// 从根节点开始,递归处理整个树
writeArray(root, 0, arrayWidth / 2, res, treeDepth);
// 此时,已经将所有需要显示的元素储存到了二维数组中,将其拼接并打印即可
for (String[] line : res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2 : line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
}
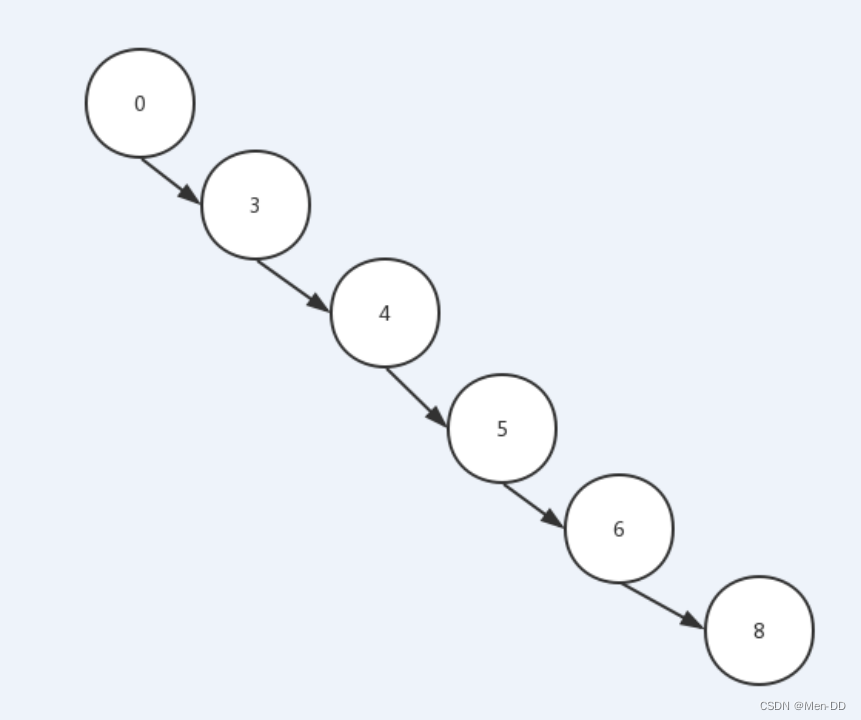
红黑树(实验室:AVL平衡二叉树)二叉搜索树退化成链表
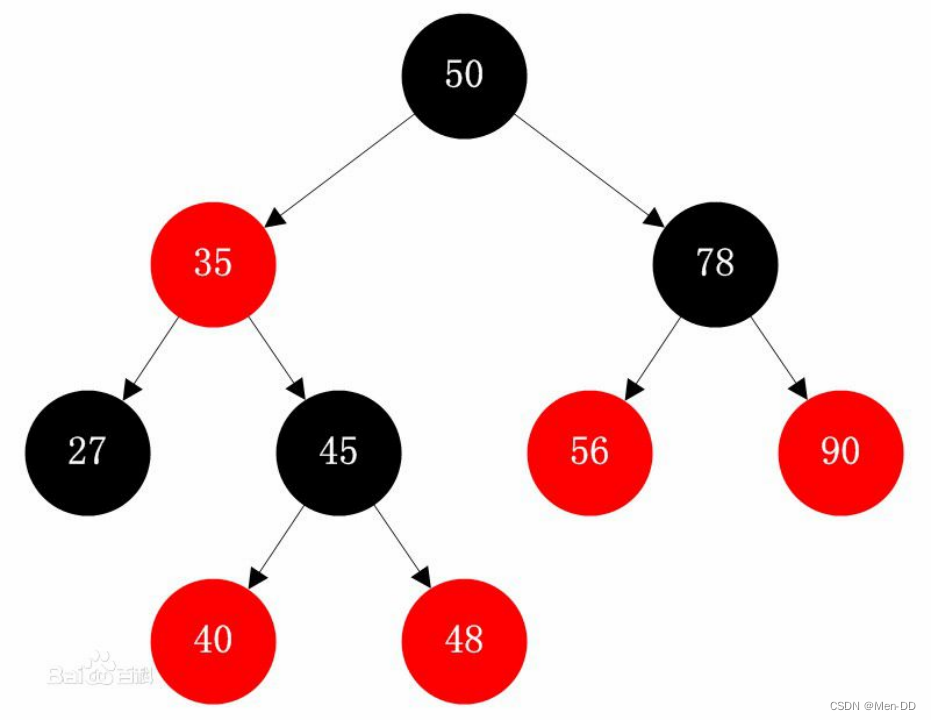
红黑树的性质:
- 每个结点不是红色就是黑色
- 不可能有连在一起的红色结点(黑色的就可以),每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据
- 根结点都是黑色 root
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点
插入的时候旋转和颜色变换规则:
- 变颜色的情况:当前结点的父亲是红色,且它的祖父结点的另一个子结点
也是红色。(叔叔结点):
(1)把父节点设为黑色
(2)把叔叔也设为黑色
(3)把祖父也就是父亲的父亲设为红色(爷爷)
(4)把指针定义到祖父结点(爷爷)设为当前要操作的. - 左旋:当前父结点是红色,叔叔是黑色的时候,且当前的结点是右子树。左旋
以父结点作为左旋。指针变换到父亲结点 - 右旋:当前父结点是红色,叔叔是黑色的时候,且当前的结点是左子树。右旋
(1)把父结点变为黑色
(2)把祖父结点变为红色 (爷爷)
(3)以祖父结点旋转(爷爷)
左旋
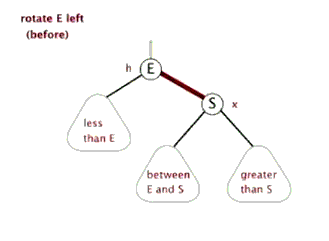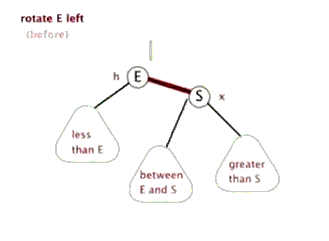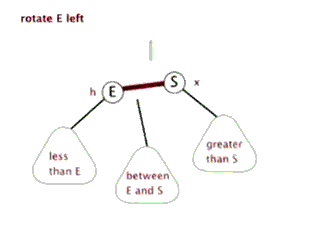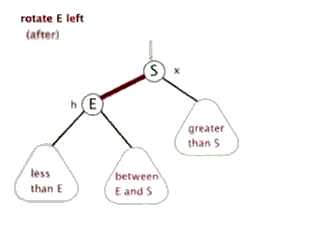
右旋
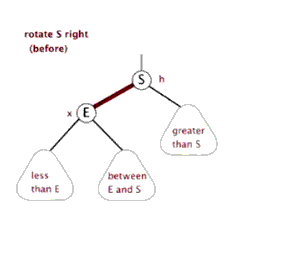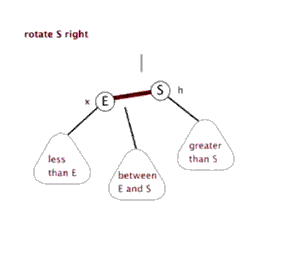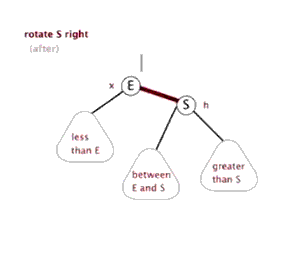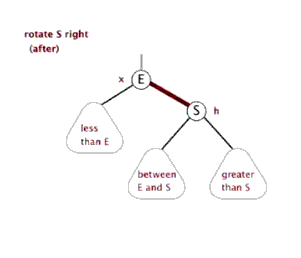
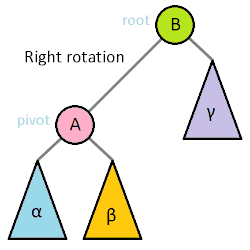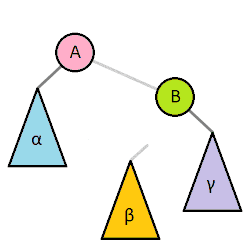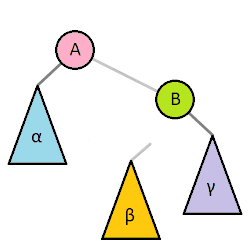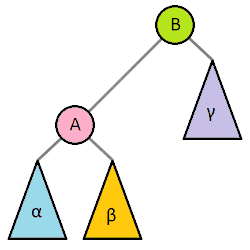
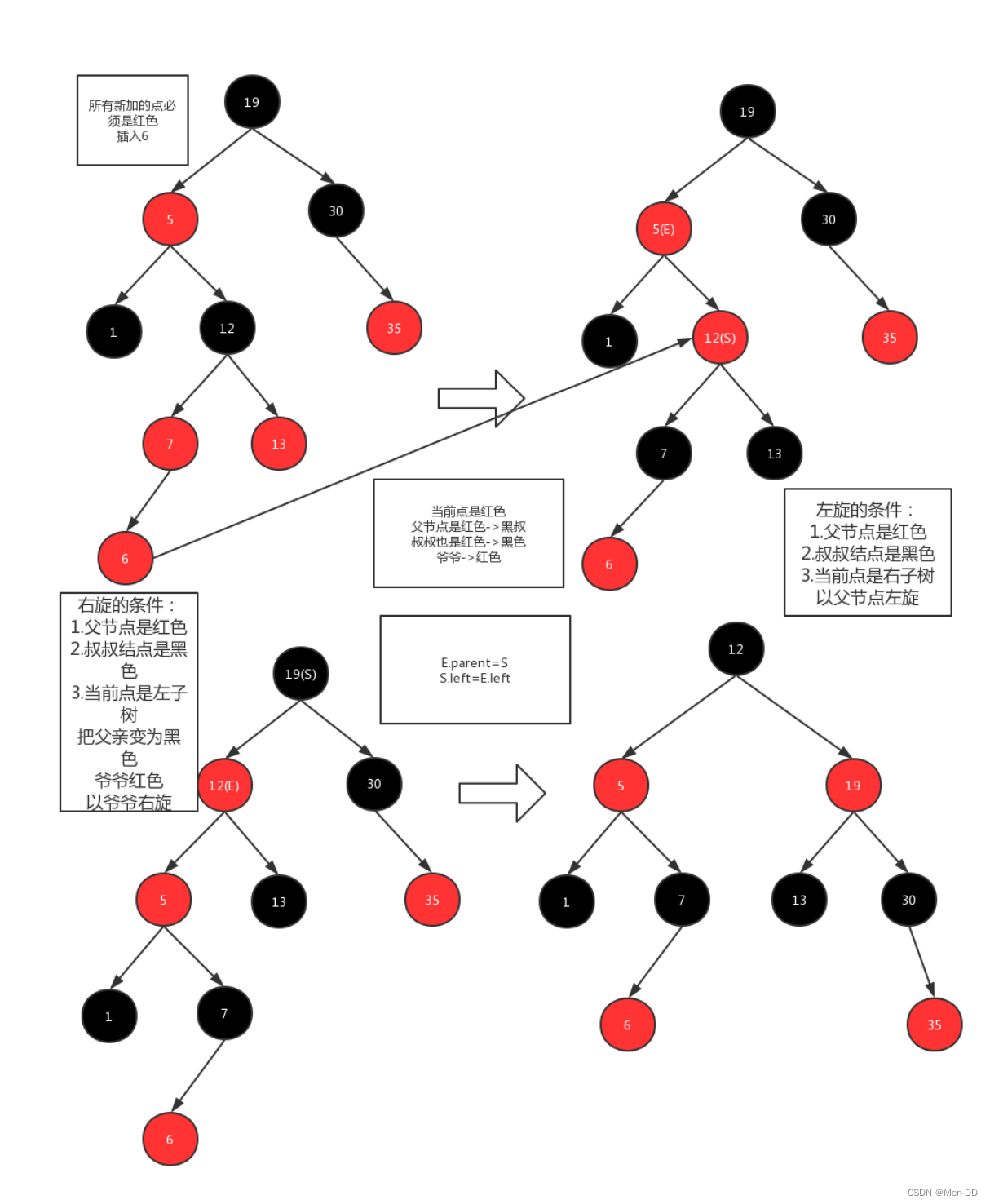
红黑树的应用
- HashMap
- TreeMap
- Windows底层:查找
- Linux进程调度,nginx等
COPY
public class RedBlackTree {
private final int R = 0;
private final int B = 1;
private class Node {
int key = -1;
int color = B; // 颜色
Node left = nil; // nil表示的是叶子结点
Node right = nil;
Node p = nil;
Node(int key) {
this.key = key;
}
@Override
public String toString() {
return "Node [key=" + key + ", color=" + color + ", left=" + left.key + ", right=" + right.key + ", p=" + p.key + "]" + "\r\n";
}
}
private final Node nil = new Node(-1);
private Node root = nil;
public void printTree(Node node) {
if (node == nil) {
return;
}
printTree(node.left);
System.out.print(node.toString());
printTree(node.right);
}
private void insert(Node node) {
Node temp = root;
if (root == nil) {
root = node;
node.color = B;
node.p = nil;
} else {
node.color = R;
while (true) {
if (node.key < temp.key) {
if (temp.left == nil) {
temp.left = node;
node.p = temp;
break;
} else {
temp = temp.left;
}
} else if (node.key >= temp.key) {
if (temp.right == nil) {
temp.right = node;
node.p = temp;
break;
} else {
temp = temp.right;
}
}
}
fixTree(node);
}
}
private void fixTree(Node node) {
while (node.p.color == R) {
Node y = nil;
if (node.p == node.p.p.left) {
y = node.p.p.right;
if (y != nil && y.color == R) {
node.p.color = B;
y.color = B;
node.p.p.color = R;
node = node.p.p;
continue;
}
if (node == node.p.right) {
node = node.p;
rotateLeft(node);
}
node.p.color = B;
node.p.p.color = R;
rotateRight(node.p.p);
} else {
y = node.p.p.left;
if (y != nil && y.color == R) {
node.p.color = B;
y.color = B;
node.p.p.color = R;
node = node.p.p;
continue;
}
if (node == node.p.left) {
node = node.p;
rotateRight(node);
}
node.p.color = B;
node.p.p.color = R;
rotateLeft(node.p.p);
}
}
root.color = B;
}
void rotateLeft(Node node) {
if (node.p != nil) {
if (node == node.p.left) {
node.p.left = node.right;
} else {
node.p.right = node.right;
}
node.right.p = node.p;
node.p = node.right;
if (node.right.left != nil) {
node.right.left.p = node;
}
node.right = node.right.left;
node.p.left = node;
} else {
Node right = root.right;
root.right = right.left;
right.left.p = root;
root.p = right;
right.left = root;
right.p = nil;
root = right;
}
}
void rotateRight(Node node) {
if (node.p != nil) {
if (node == node.p.left) {
node.p.left = node.left;
} else {
node.p.right = node.left;
}
node.left.p = node.p;
node.p = node.left;
if (node.left.right != nil) {
node.left.right.p = node;
}
node.left = node.left.right;
node.p.right = node;
} else {
Node left = root.left;
root.left = root.left.right;
left.right.p = root;
root.p = left;
left.right = root;
left.p = nil;
root = left;
}
}
public void creatTree() {
int data[]= {23,32,15,221,3};
Node node;
System.out.println(Arrays.toString(data));
for(int i = 0 ; i < data.length ; i++) {
node = new Node(data[i]);
insert(node);
}
printTree(root);
}
/**
* [23, 32, 15, 221, 3]
* Node [key=3, color=0, left=-1, right=-1, p=15]
* Node [key=15, color=1, left=3, right=-1, p=23]
* Node [key=23, color=1, left=15, right=32, p=-1]
* Node [key=32, color=1, left=-1, right=221, p=23]
* Node [key=221, color=0, left=-1, right=-1, p=32]
*/
public static void main(String[] args) {
RedBlackTree bst = new RedBlackTree();
bst.creatTree();
}
}
Btree&B+Tree
B-Tree和B+Tree的区别
- B-tree所有的节点都会存数据
- b-tree叶子节点没有链表
数据库索引是什么样的数据结构呢?它为什么又能这么高效的查找呢?究竟使用了什么样的算法呢?
select * from table where id = 10
select * from table where id > 12
select * from table where id > 12 and id < 20
改造二叉搜索树:
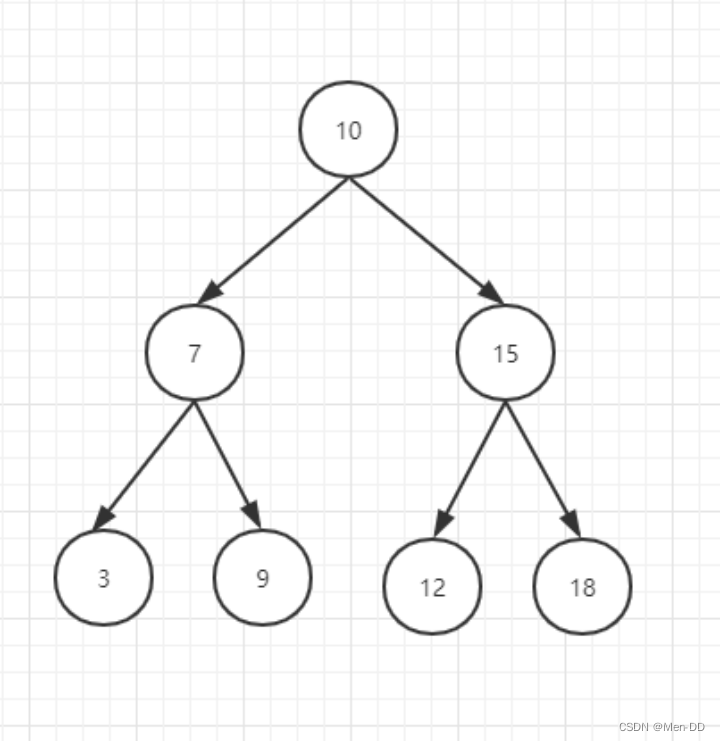
能解决我们上面所有的sql语句;
效率 logn
2^32=21亿;
IO:指的是从磁盘读取数据。32层就要读取32次。CPU,内存,IO;
IO从磁盘读一次会读多少数据?计算机组成原理。Page的。页,4KB
Int占多少空间?4B
思考
问题1:搜索效率:32次 (B+Tree 多叉树)
问题2:查询次数: (B+Tree 范围 )
问题3:磁盘IO:解决这个问题;(B+Tree 只有叶子节点存储数据地址)
B+Tree 数据结构
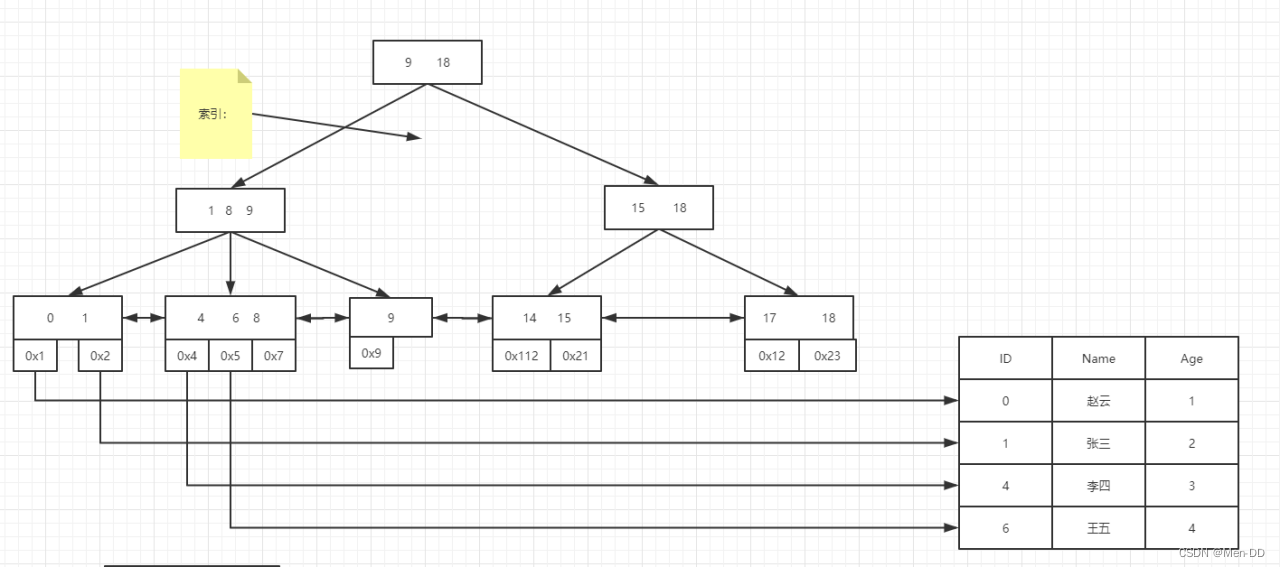
Mysql 如何利用B+Tree 解决问题
Mysql 通过页大小决定,一般是16kb,一个bigint主键类型创建索引消耗的空间是多少?
int 8 字节,指针一个算4字节,一页的节点:16kb/(8+8)=1k 键值+指针
三阶:102410241024=10 7374 1824
如何正确的建立索引:
- 索引不能太多,因为B+tree的插入和删除是要维护的,太多的索引会导致插入变慢。
- 建了索引的字段不能使用like ‘%%’否则是失效的
- 建索引的字段类型不能太大,字段越小阶数就越大,效率就越高,int 和 bigint,varchar(10),varchar(100),text,lontext;B+Tree。全文索引
- 建索引的字段值不能太多一样的,数学里面有个叫什么散列多一些(离散),比如我们把性别建索引会出现啥情况?左边都是一样的值 过滤不了一半。User sex单独建索引 0 1
- 联合索引的最左匹配原则。Select * from user where name = ‘mx’ and id = 1 我的对( id,name)建的索引,mysql解析的时候会自动优化。
Select * from user where name = ‘mx’ and age=10我的对( id,name,age)建的索引 - NOT IN 是不会走索引的 not in (1,2,3) In的值太多 mysql会报错的
赫夫曼树(哈夫曼树、哈夫曼编码、前缀编码)-- 压缩软件、通信电报
电报的设计:
1.电报加密后越短越好,发送快
2.破解难
3.解码容易
4.换加密树也要快
5.可逆的
计算下面三颗二叉树的带权路径长度总和:
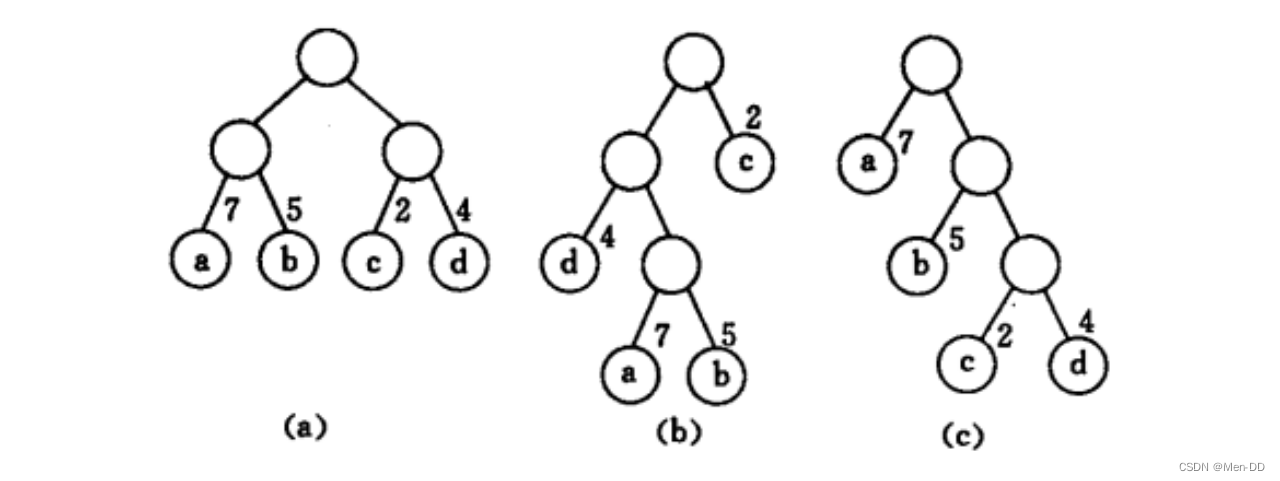
WPL(a):7*2+5*2+2*2+4*2=36()
WPL(b):7*3+5*3+2*1+4*2=46()
WPL(c):7*1+5*2+2*3+4*3=35()
左节点的边设置为0
右节点的边设置为1
© 哈夫曼编码就是
A:0
B:10
C:110
D:111
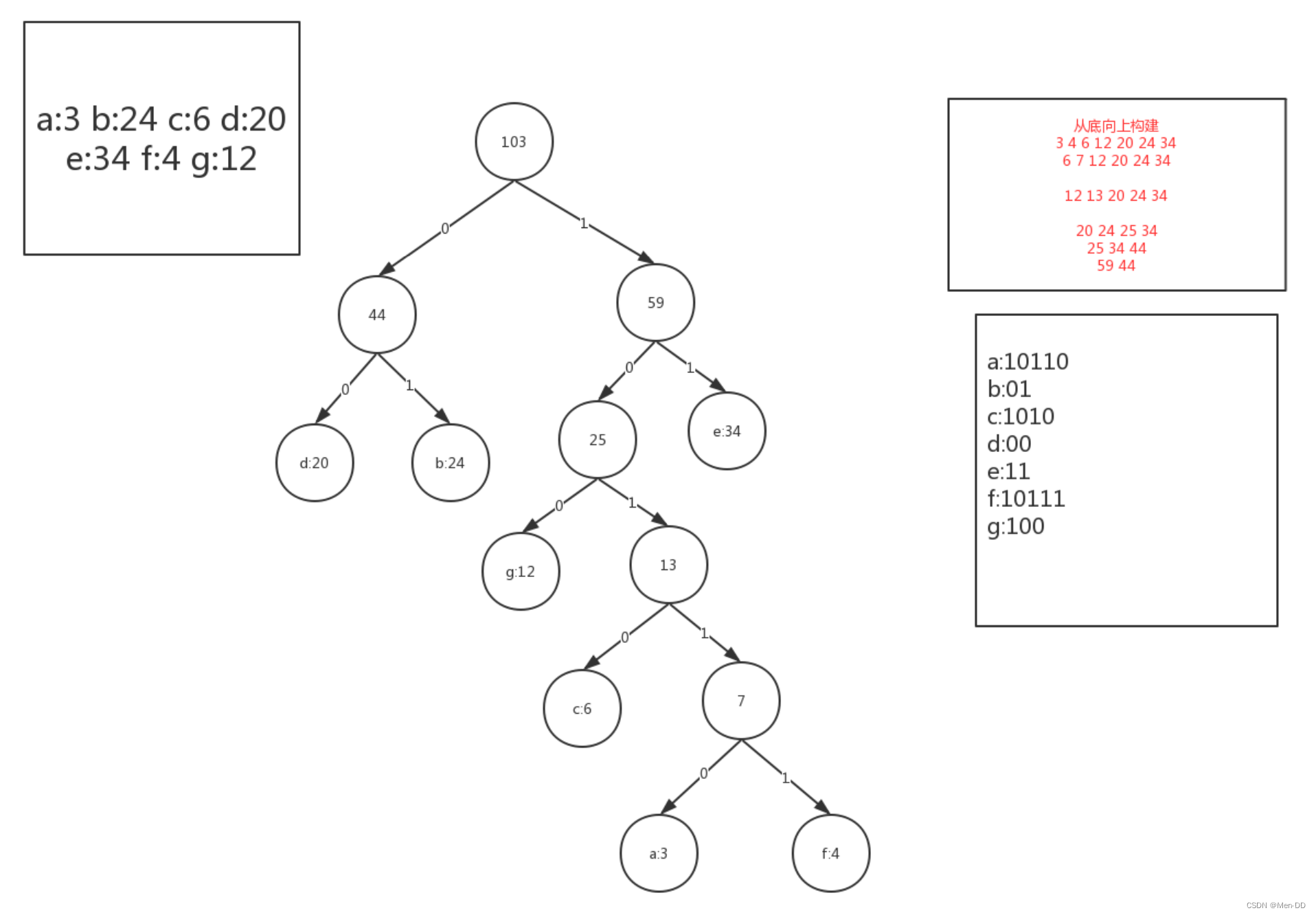
构建哈夫曼树:
1.每次取数值最小的两个节点,将之组成为一颗子树。
2.移除原来的两个点
3.然后将组成的子树放入原来的序列中
4.重复执行1 2 3 直到只剩最后一个点
/**
* 赫夫曼树
*/
class HuffmanNode implements Comparable<HuffmanNode> {
String chars;
int fre; //频率 权重
HuffmanNode parent;
HuffmanNode left;
HuffmanNode right;
@Override
public int compareTo(HuffmanNode o) {
return this.fre - o.fre;
}
}
public class HuffmanTree {
HuffmanNode root;
List<HuffmanNode> leafs; //叶子节点
Map<Character, Integer> weights; //叶子节点
Map<Character, String> charmap;
Map<String, Character> mapchar;
public HuffmanTree(Map<Character,Integer> weights) {
this.weights = weights;
leafs = new ArrayList<>();
charmap = new HashMap<>();
mapchar = new HashMap<>();
}
public void code() {
for (HuffmanNode node : leafs) {
Character c = new Character(node.chars.charAt(0));
HuffmanNode current = node;
String code = "";
do {
if (current.parent != null && current == current.parent.left) { //left
code = "0" + code;
} else {
code = "1" + code;
}
current = current.parent;
} while (current.parent != null);
charmap.put(c, code);
mapchar.put(code, c);
}
}
public void createTree() {
Character keys[] = weights.keySet().toArray(new Character[0]);
PriorityQueue<HuffmanNode> priorityQueue = new PriorityQueue<>();
for (Character key : keys) {
HuffmanNode huffmanNode = new HuffmanNode();
huffmanNode.chars = key.toString();
huffmanNode.fre = weights.get(key);
priorityQueue.add(huffmanNode);
leafs.add(huffmanNode);
}
int len = priorityQueue.size();
for (int i = 1; i <= len-1; i++) {
HuffmanNode n1 = priorityQueue.poll();
HuffmanNode n2 = priorityQueue.poll();
HuffmanNode newNode = new HuffmanNode();
newNode.fre = n1.fre + n2.fre;
newNode.chars = n1.chars + n2.chars;
newNode.left = n1;
newNode.right = n2;
n1.parent = newNode;
n2.parent = newNode;
priorityQueue.add(newNode);
}
root = priorityQueue.poll();
}
public String encode(String body) {
StringBuilder builder = new StringBuilder();
for (char c : body.toCharArray()) {
builder.append(charmap.get(c));
}
return builder.toString();
}
public String decode(String body) {
StringBuilder builder = new StringBuilder();
while (!body.equals("")) {
for (String code : mapchar.keySet()) {
if (body.startsWith(code)) {
body = body.replaceFirst(code,"");
builder.append(mapchar.get(code));
}
}
}
return builder.toString();
}
/**
* a : 10110
* b : 01
* c : 1010
* d : 00
* e : 11
* f : 10111
* g : 100
* encode: 0010111101111010
* decode: dffc
*/
public static void main(String[] args) {
Map<Character, Integer> weights = new HashMap<>();
weights.put('a',3);
weights.put('b',24);
weights.put('c',6);
weights.put('d',20);
weights.put('e',34);
weights.put('f',4);
weights.put('g',12);
HuffmanTree huffmanTree = new HuffmanTree(weights);
huffmanTree.createTree();
huffmanTree.code();
for (Map.Entry<Character, String> entry : huffmanTree.charmap.entrySet()) {
System.out.println(entry.getKey() + " : " + entry.getValue());
}
String encode = huffmanTree.encode("dffc");
System.out.println("encode: " + encode);
String decode = huffmanTree.decode(encode);
System.out.println("decode: " + decode);
}
}
堆树
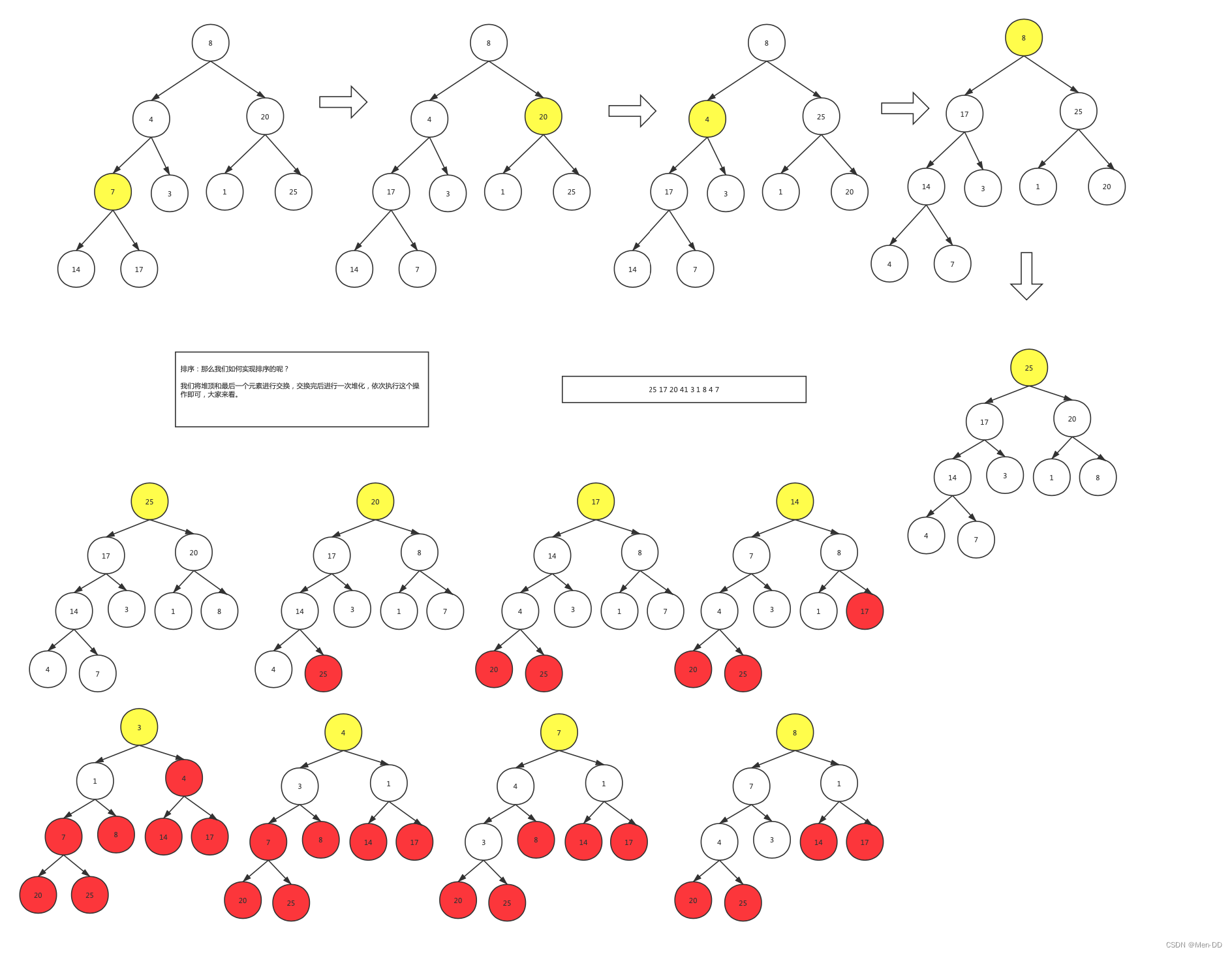
假设给你一个序列:8 4 20 7 3 1 25 14 17
利用堆树进行排序:
- 先按照序列顺序存储在完全二叉树中:建堆
- 从最后一个非叶子节点堆化。为什么是最后一个非叶子节点而不是最后一个叶子节点呢?(最后叶子节点没有左右节点无法比较)
堆的插入有两种实现方式:
- 从下往上
- 从上往下
其插入过程就叫做堆化
**
* 堆树
*
* 建堆
* 排序
*
* 1. 优先级队列问题: 删除最大的
* 2. top n 热搜排行榜问题:1000万的数字
* 3. 定时器 堆顶
* 4. 给你1亿不重复的数字,求出top10,前10最大的数字,还可动态添加
*/
public class HeapTree {
//建大顶堆
public static void maxHeap(int data[], int parent, int end) {
int leftSon = parent * 2 + 1; //下标从0开始+1
while (leftSon < end) {
int temp = leftSon;
//temp表示的是 我们左右节点大的那一个
if (leftSon + 1 < end && data[leftSon] < data[leftSon + 1]) {
temp = leftSon + 1; //右节点比左节点大
}
//比较左右节点大的那一个temp和父节点比较大小
if (data[parent] > data[temp]) {
return; //不需要交换
} else {
int t = data[parent]; //交换
data[parent] = data[temp];
data[temp] = t;
parent = temp; //继续堆化
leftSon = parent * 2 + 1;
}
}
}
public static void heapSort(int data[]) {
int len = data.length;
//从后向上建
//建堆从哪里开始 最后一个的父元素开始(len/2 - 1)(父元素中:最后一个父元素是第几个,从0开始)
for (int parent = len/2 - 1; parent >= 0; parent--) { //nlog(n)
maxHeap(data, parent, len);
}
//从上向下建
//最后一个数和第一个数交换
int headHeap = 0;
for (int tailHeap = len - 1; tailHeap > 0; tailHeap--) { //nlog(n)
int temp = data[headHeap];
data[headHeap] = data[tailHeap];
data[tailHeap] = temp;
maxHeap(data, headHeap, tailHeap);
}
}
/**
* Arrays: [1, 3, 4, 7, 8, 14, 17, 20, 25]
*/
public static void main(String[] args) {
int data[] = {8, 4, 20, 7, 3, 1, 25, 14, 17};
heapSort(data);
System.out.printf("Arrays: " + Arrays.toString(data));
}
}
topK
class TopK {
private int k = 10;
private int data[] = new int[k];
public void topK() {
Random random = new Random();
long time = System.currentTimeMillis();
int size = 0;
boolean init = false;
for (int i = 0; i < 100000000; i++) {
int num = random.nextInt(100000000);
if (size < k) {
data[size] = num;
size++;
} else {
if (!init) {
for (int j = k/2 - 1; j >=0; j--) {
minHeap(data, 0, k);
}
init = true;
}
if (num > data[0]) {
data[0] = num;
minHeap(data, 0, k);
}
}
}
System.out.println("耗时:" + (System.currentTimeMillis() - time) + "ms \n");
for (int datum : data) {
System.out.print(datum+", ");
}
}
private void minHeap(int[] data, int start, int end) {
int parent = start;
int son = parent * 2 + 1;
while (son < end) {
int temp = son;
if (son + 1 < end && data[son] > data[son +1]) { //右节点比左节点大
temp = son + 1; //根号右节点和父节点
}
//temp表示我们左右节点小的那一个
if (data[parent] < data[temp]) {
return;
} else {
int t = data[parent];
data[temp] = t;
parent = temp;
son = parent * 2 + 1;
}
}
return;
}
public static void main(String[] args) {
TopK topK = new TopK();
topK.topK();
}
}