【Python】值得收藏，三元一次方程组的计算，快来看看有什么新奇的~~~

news2025/1/22 9:04:52

三元一次方程组的计算对于大家来说都不陌生了，但是用编程语言来解决方程组问题想必还是会有些大聪明们有点迷糊的，今天就带大家来看看是怎么利用python实现方程组的解集的；
本文主要分成两部分：

解题
验算
综述

解题

题目1

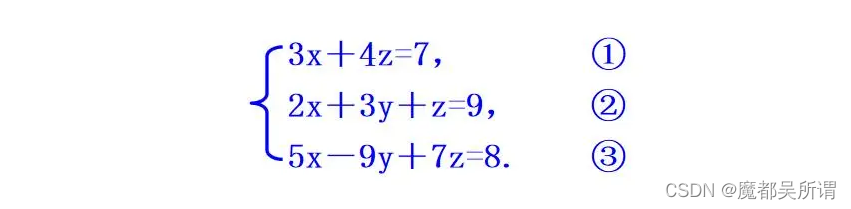
在这里插入图片描述

代码

import numpy as np

para_1 = [[3, 0, 4], [2, 3, 1], [5, -9, 7]]
result_1 = [7, 9, 8]

# 新建矩阵
A = np.mat(para_1)
print(A)
# 常数矩阵
b = np.array(result_1)
print(b)
# 求解
dt = np.linalg.solve(A, b)
print("计算结果： ", dt)
print("===="*30)
print(dt[0])
print(dt[1])
print(dt[2])

结果

[[ 3 0 4]
[ 2 3 1]
[ 5 -9 7]]
[7 9 8]
计算结果： [ 5. 0.33333333 -2. ]
================================================================================
5.000000000000002
0.33333333333333265
-2.000000000000002

手算结果

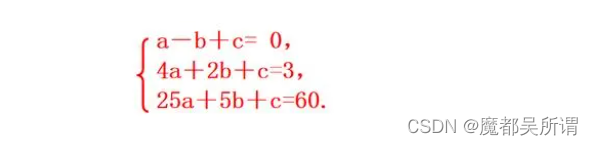
在这里插入图片描述

题目2

在这里插入图片描述

代码

import numpy as np

para_2 = [[1, -1, 1], [4, 2, 1], [25, 5, 1]]
result_2 = [0, 3, 60]
# 新建矩阵
A = np.mat(para_2)
print(A)
# 常数矩阵
b = np.array(result_2)
print(b)
# 求解
dt = np.linalg.solve(A, b)
print("计算结果： ", dt)
print("===="*30)
print(dt[0])
print(dt[1])
print(dt[2])

结果

[[ 1 -1 1]
[ 4 2 1]
[25 5 1]]
[ 0 3 60]
计算结果： [ 3. -2. -5.]
===============================================================================
3.0
-1.9999999999999996
-5.000000000000001

手算结果

在这里插入图片描述

验算

借助np.dot()方法进行验算；
分别围绕两道题目展开验算；

题目1

import numpy as np

# 新建矩阵
A = np.mat(para_1)
print(A)
# 常数矩阵
b = np.array(result_1)
print(b)
# 求解
dt = np.linalg.solve(A, b)
print(dt)
# 验算
print(np.dot(A, dt))

[[ 3 0 4]
[ 2 3 1]
[ 5 -9 7]]
[7 9 8]
[ 5. 0.33333333 -2. ]
[[7. 9. 8.]]

题目2

import numpy as np

# 新建矩阵
A = np.mat(para_2)
print(A)
# 常数矩阵
b = np.array(result_2)
print(b)
# 求解
dt = np.linalg.solve(A, b)
print(dt)
# 验算
print(np.dot(A, dt))

结果