信息收集(一)域名信息收集
什么是CDN?
内容分发网络(CDN): 是指企业利用分布在不同区域的节点服务器群组成流量分配管理平台,为用户提供内容分散存储和高速缓存服务
在渗透测试过程中,经常会碰到网站有CDN的情况。CDN即内容分发网络,主要解决因传输距离和不同运营商节点造成的网络速度性能低下的问题。说的简单点,就是一组在不同运营商之间的对接点上的高速缓存服务器,把用户经常访问的静态数据资源直接缓存到节点服务器上,当用户再次请求时,会直接分发到离用户近的节点服务器上响应给用户,当用户有实际数据交互时才会从远程Web服务器上响应,这样可以大大提高网站的响应速度及用户体验
CDN的优势
- 提高用户访问速率,优化用户使用体验
- 隐藏真实服务器的IP
- 提供WAF功能,目前很多CDN也提供了WAF的功能,我们的访问请求会先经过CDN节点的过滤,该过滤可对SQL注入、XSS、Webshell上传、命令注入、恶意扫描等攻击行为进行有效检测和拦截。CDN节点将认为无害的数据提交给真实的主机服务器。
CDN几种访问方式的不同
- 传统访问:用户访问域名–>解析服务器IP–>访问目标主机
- 普通CDN:用户访问域名–>CDN节点–>真实服务器IP–>访问目标主机
- 带WAF的CDN:用户访问域名–>CDN节点(云WAF)–>真实服务器IP–>访问目标主机
没有CDN:
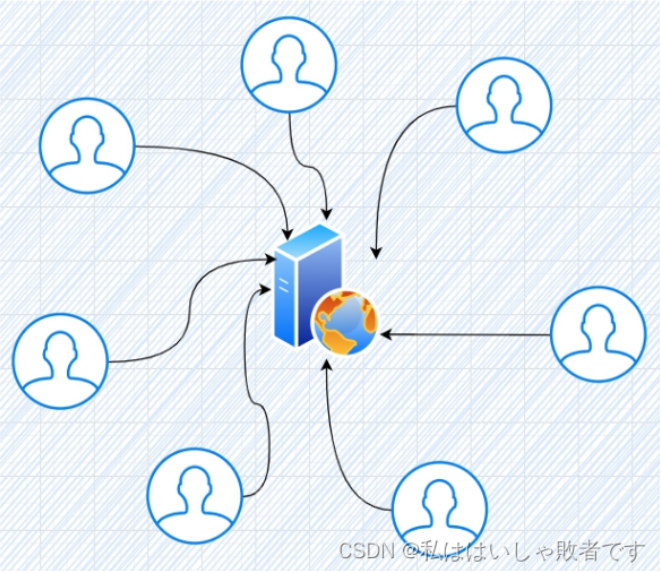
使用CDN服务:
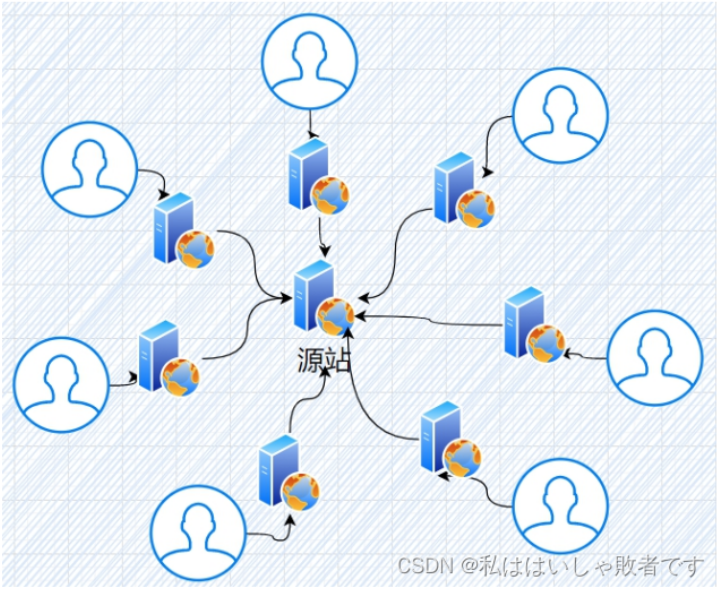
所以在渗透测试中,为了要知道网站服务器的真实IP,我们必须绕过CDN查找出网站的真实ip地址
如何判断目标网站有没有使用CDN
1、我们可以使用nslookup来判断目标网站有没有使用CDN
nslookup www.baidu.com
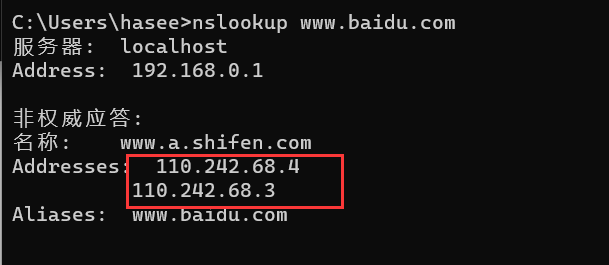
如上图给出了两个或两个以上地址的应答,就说明目标网站很可能使用了CDN服务
2、SearchMap判断目标有没有使用CDN
searchmap是一款集域名解析、IP反查域名、WHOIS查询、CDN检测、端口扫描、目录扫描、子域名挖掘为一体的前渗透测试综合信息收集工具
下载地址:SearchMap下载
下载好SearchMap后使用以下命令安装依赖
python3 -m pip install -r requirements.txt
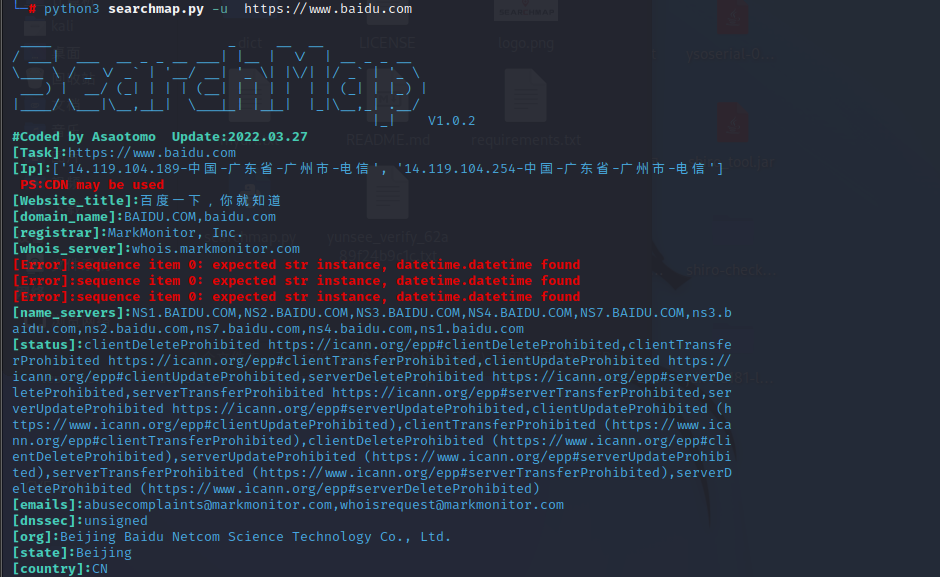
1.获取网站基本信息
python3 searchmap.py -u https://www.baidu.com
python3 searchmap.py -u 106.53.143.192
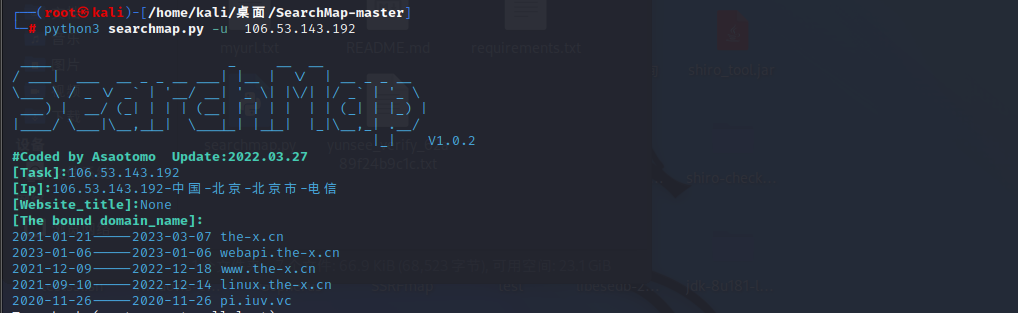
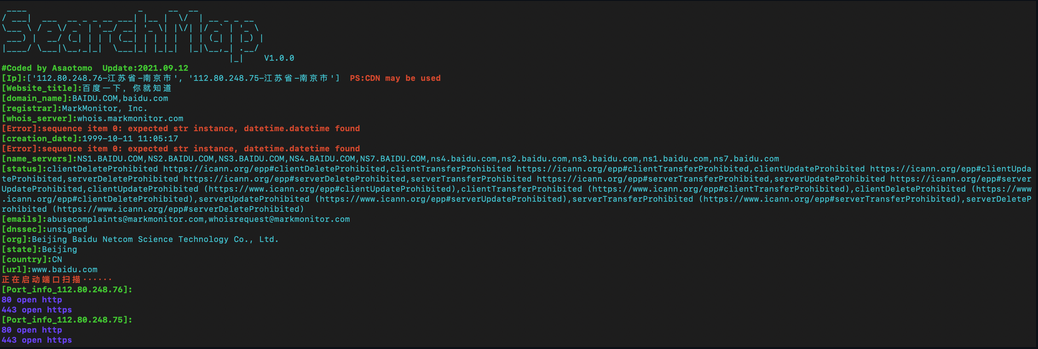
2.使用nmap进行隐式端口扫描
python3 searchmap.py -u https://www.baidu.com -p
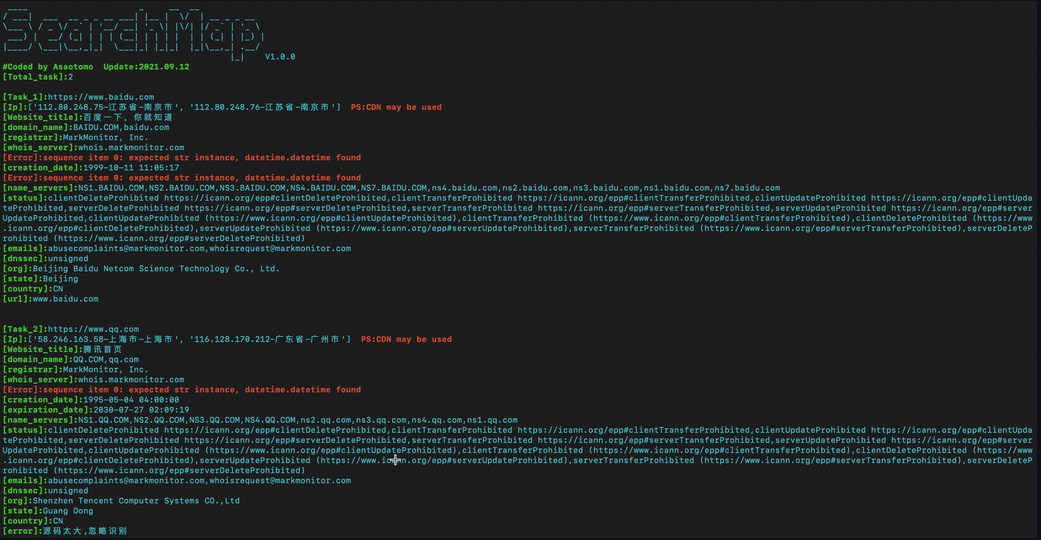
3.批量扫描网站基本信息
python3 searchmap.py -r myurl.txt
4.使用多地ping来判断目标是否使用cdn加速
python3 searchmap.py -u https://www.baidu.com -n
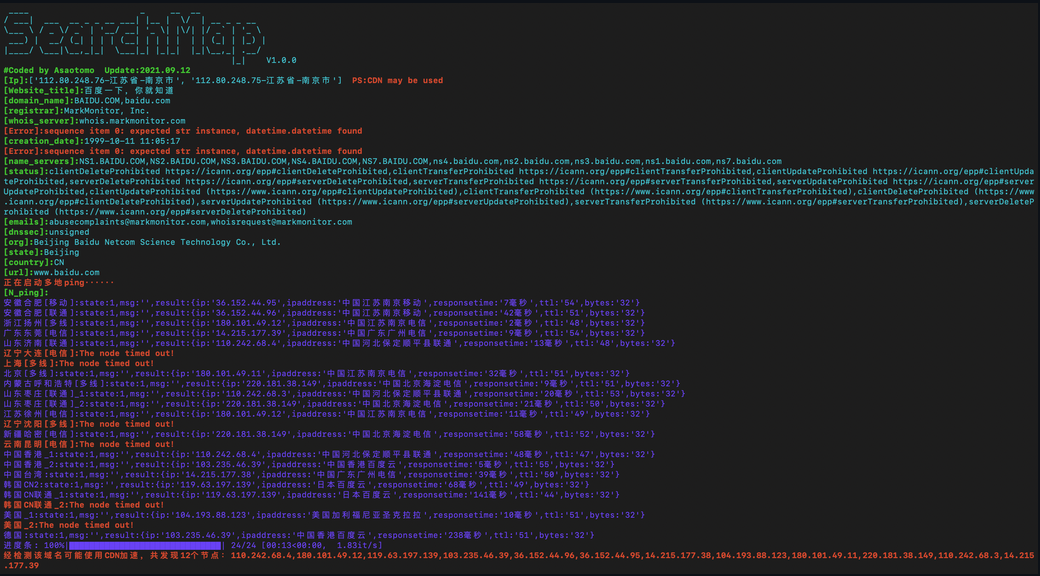
如何绕过CDN找寻真实IP
那么在渗透测试的过程中我们该如何绕过CDN去找寻真实的IP呢?
1、通过域名解析记录
通过域名解析记录指向服务器,通过历史域名解析的记录就可以去查询一些网站的真实IP,一些网站在开始起家时,是没有使用CDN技术的,很可能是近几年才开始使用CDN技术的,如果你去查询这些网站所有的解析记录,甚至可以查询到刚开始这个网站没有使用CDN时的域名解析记录,那这时查出来的地址很可能就是真实IP
IP History - ViewDNS.info
网站地址:https://viewdns.info/iphistory/
像我们这里去查询百度的域名解析记录
百度的域名解析记录结果如下
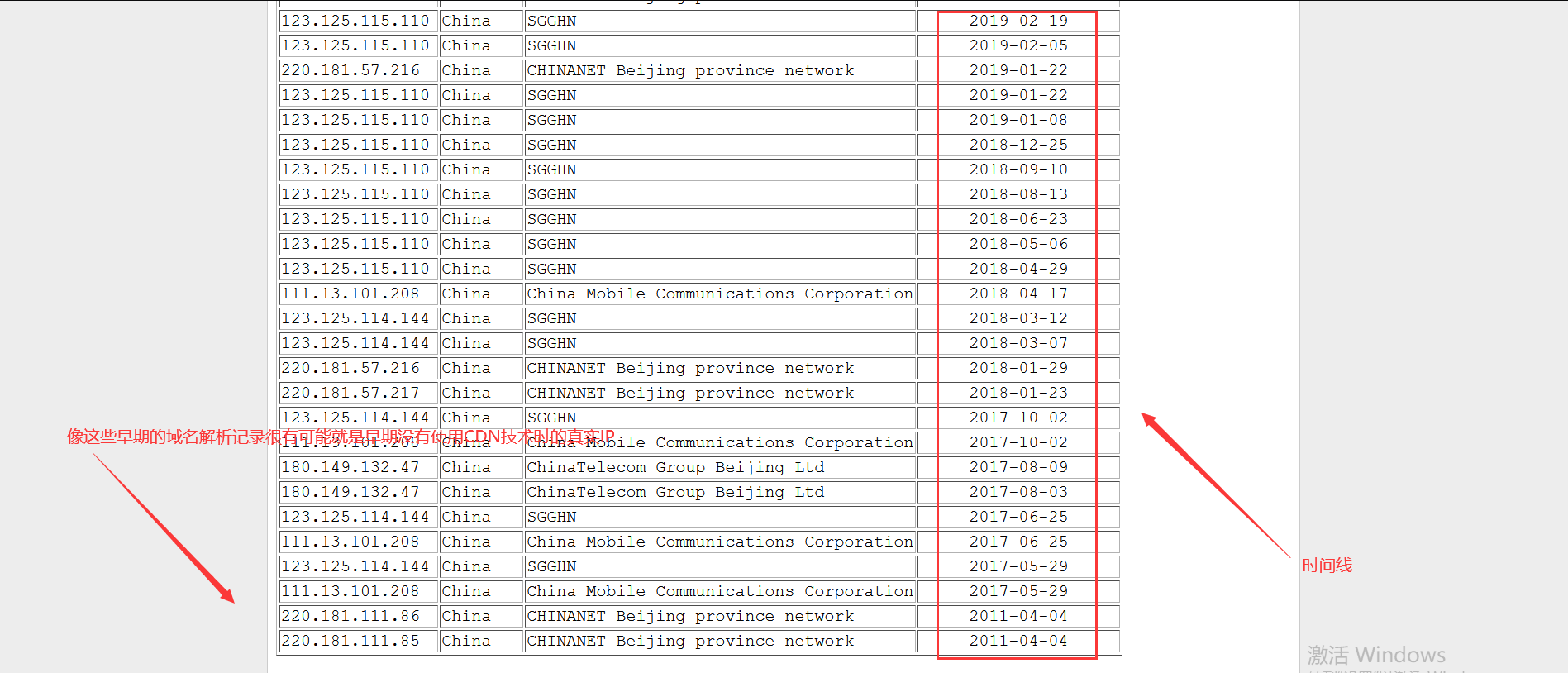
2、通过空间安全搜索引擎
什么是网络空间搜索引擎?交换机、路由器、网络摄像头、私人网盘、打印机、ATM、物联网家电等等。这些所有的系统和设备,就是网络里面的一个个节点,共同组成了网络空间我们想直接通过引擎去搜索网络上的这些硬件设备 就有了网络空间搜索引擎
fofa网络空间搜索引擎
网站地址:https://fofa.info/
国产的网络空间搜索引擎,由白帽汇推出
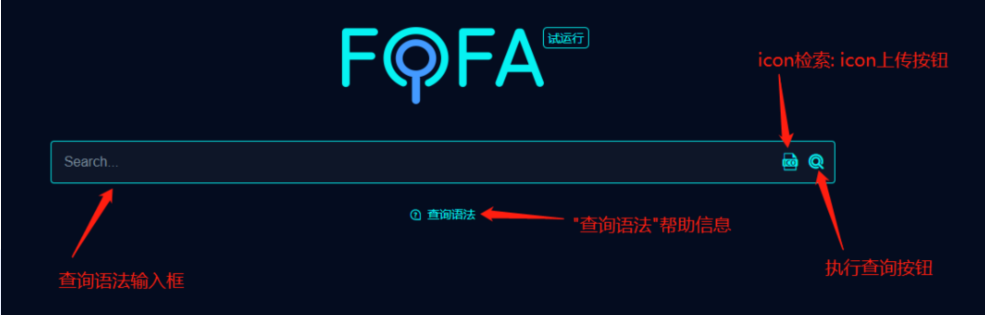
像我们去用网络空间搜索引擎去搜索真实的IP可以借用证书的序列号去搜索
以下我们来做个演示:
我们来查看百度证书的序列号
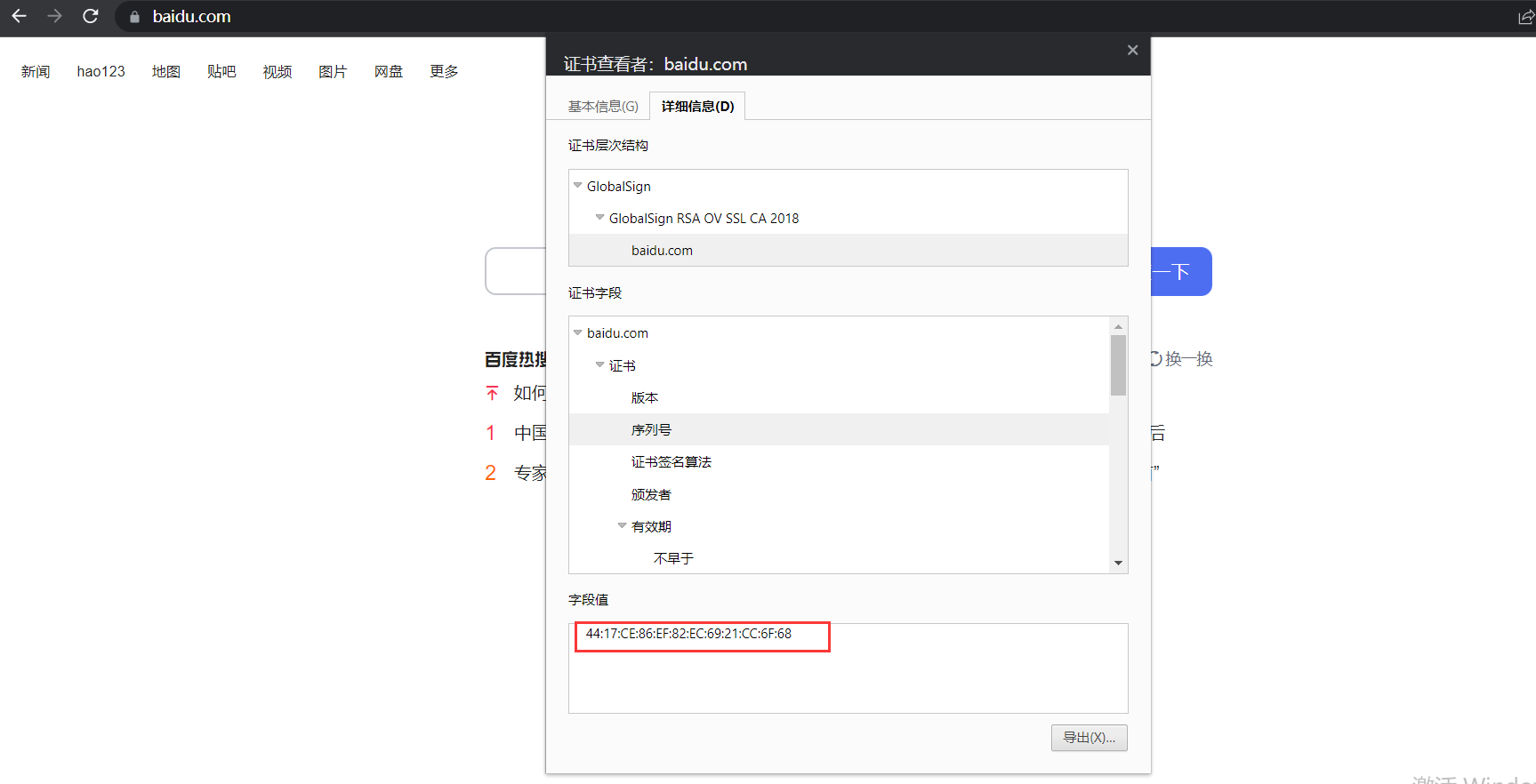
将其复制下来,转换为十进制的结果
进制转换网站:https://tool.lu/hexconvert/
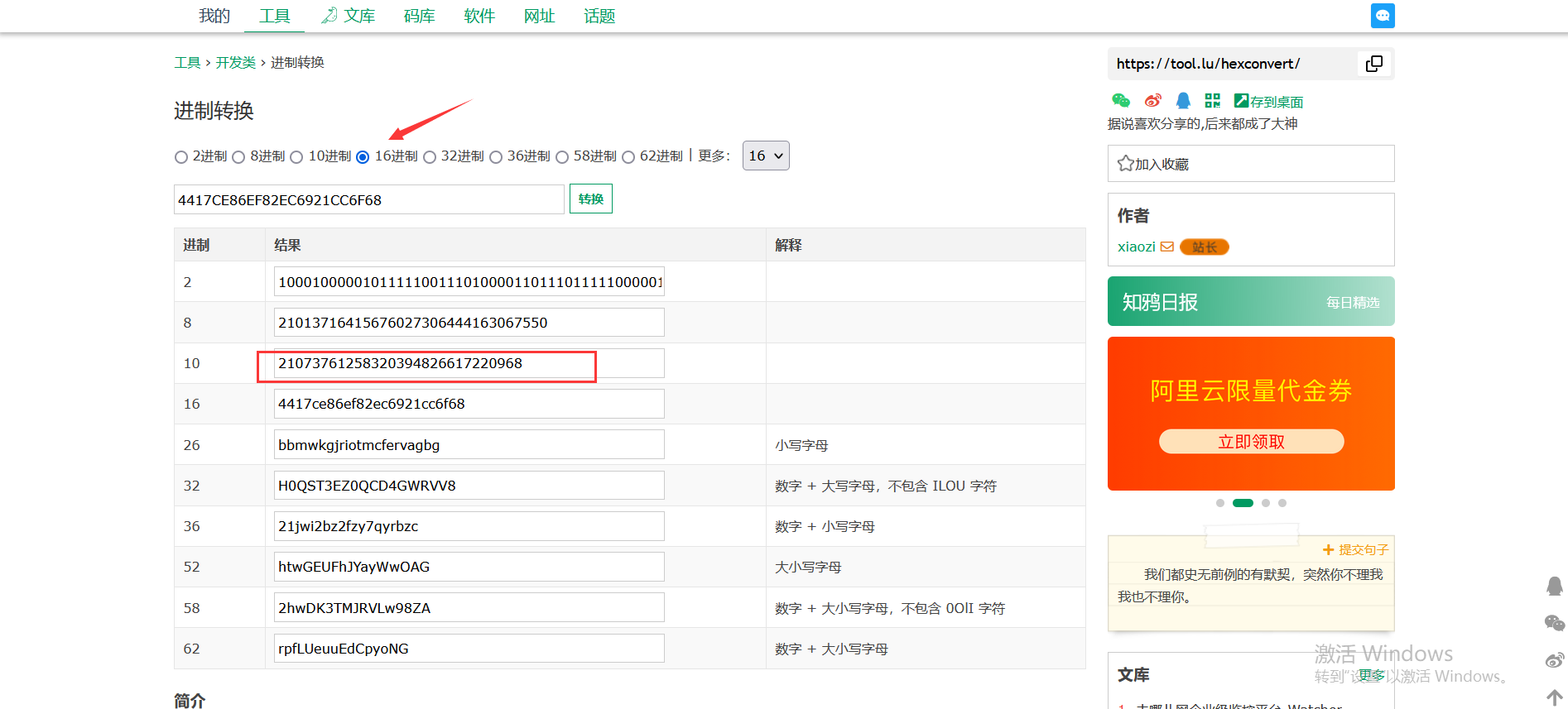
然后通过fofa引擎去搜索序列号,这时出来的网站很有可能就是一些真实的IP
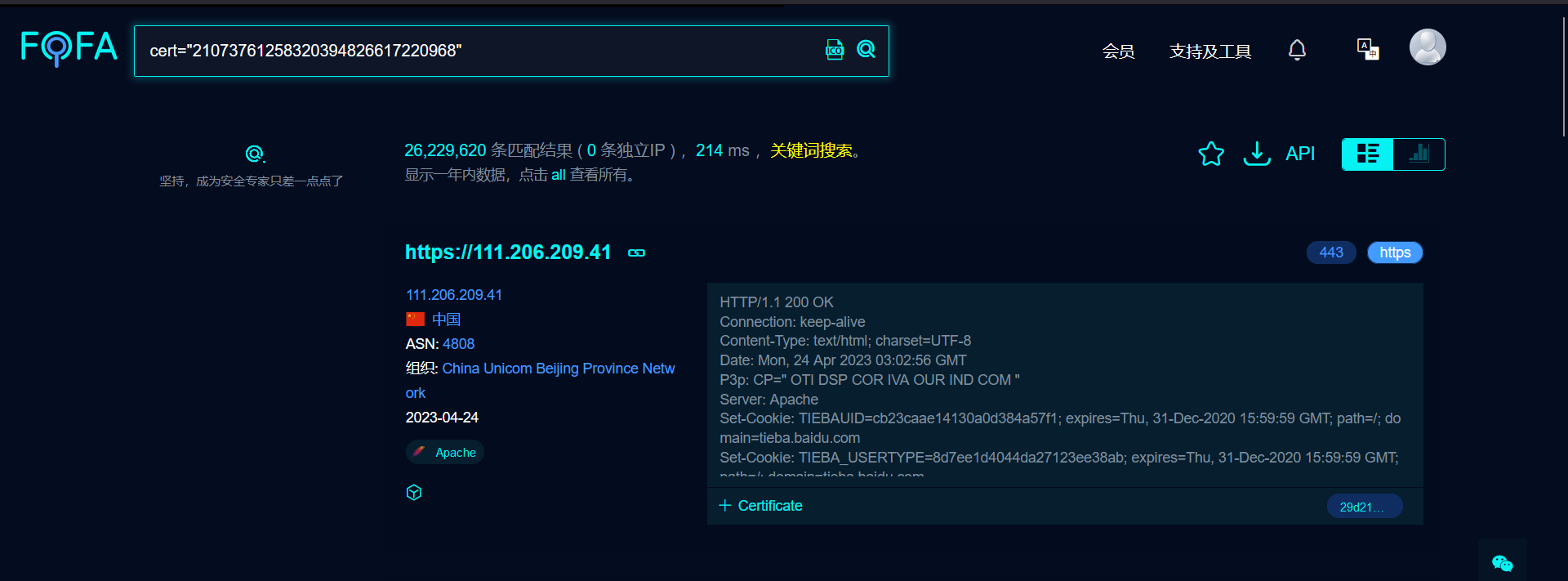
shodan网络空间搜索引擎
网站地址:https://www.shodan.io/
鹰图网络空间搜索引擎
网站地址:https://hunter.qianxin.com/

censys网络空间搜索引擎
网站地址:https://search.censys.io/

zoomeye 钟馗之眼网络空间搜索引擎
网站地址:https://www.zoomeye.org/
360quake网络空间搜索引擎
网站地址:https://quake.360.cn/quake/