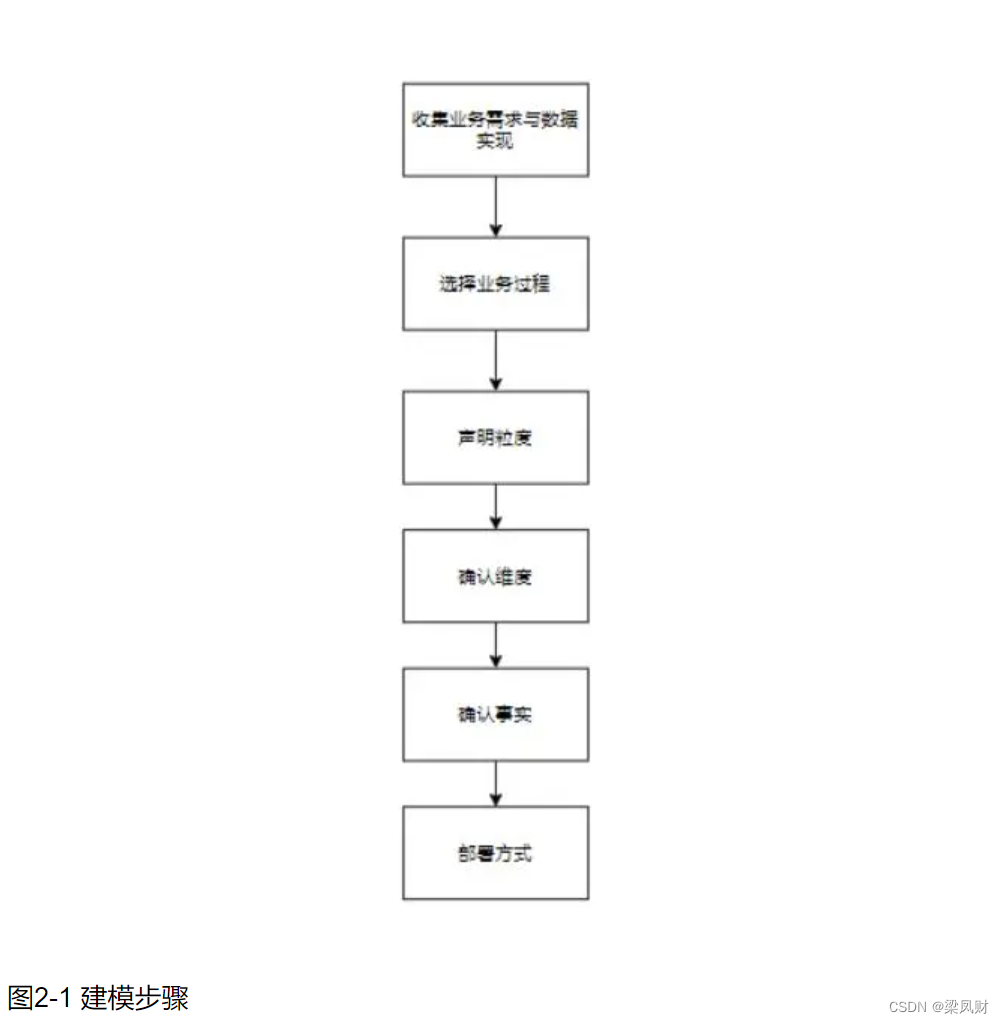
一、牛顿迭代公式

1、定义

 2、原理推导

 泰勒公式：

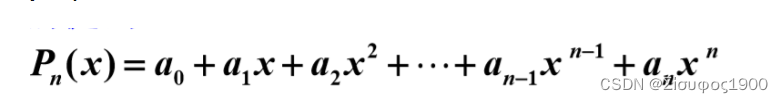
 常用的8个泰勒公式：

 推导：

将f(x)=f(x)在Xk 处的泰勒公式展开：

f(x)=f(Xk)+f(Xk)`(X-Xk)+    f(Xk)`/2  *(x-Xk)^2+..........

我们吧线性的一部分先拿出来：f(x)=f(Xk)+f(Xk)`(X-Xk) =0；

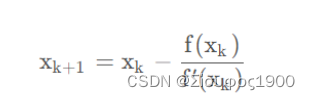
 3、几何意义

盗图：

MATLAB之牛顿迭代法_newton迭代法 matlab_天涯铭的博客-CSDN博客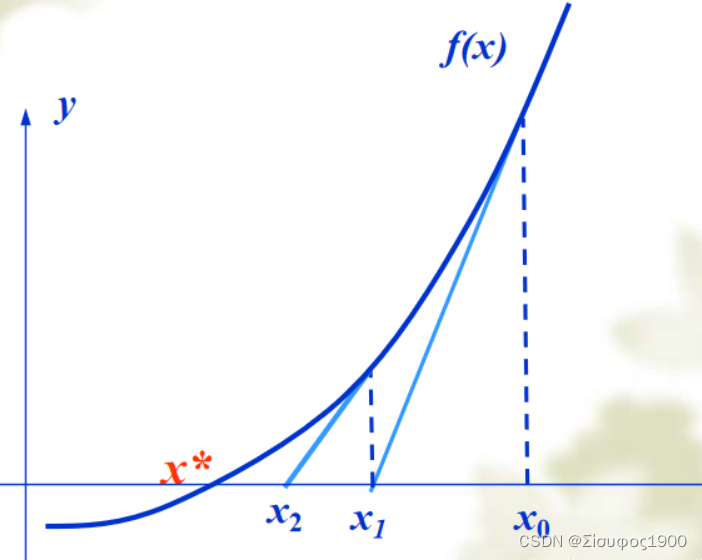

 图中直线表示的是在x0出的斜率，可以表示为：

f(x)`=f(x)/x0-x1

化简后得到：  x1=x0-f(x0)/f(x)`

4、牛顿法的收敛条件

若 x在【a，b】区间是2连续的，那么牛顿法的条件如下：

a、f(a)*f(b)<0;

b、f(x)`!=0

c、f(x)``在【a,b】区间上是同符号

d、f(x)``*f(x0)>0  .x0在【a,b】;

牛顿迭代法的收敛性取决于x0的选择，所以x0的选取很重要

 

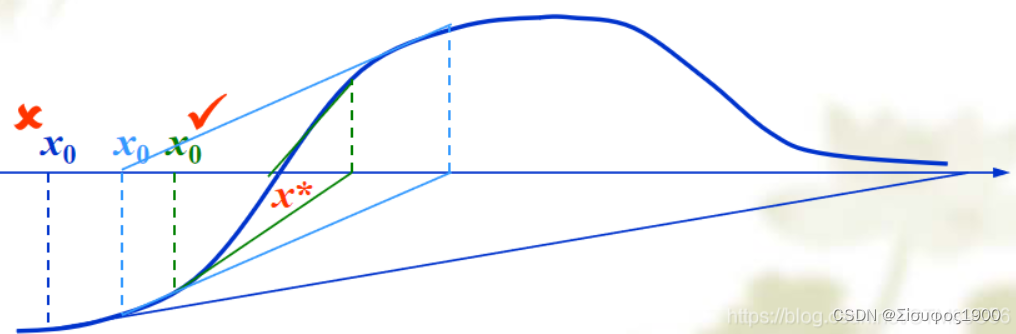
 二、算法流程

 eg:f(x)=x^3−x 

数值分析——Newton迭代法求解方程附Matlab程序_用newton法求方程_Edword_adra的博客-CSDN博客s

这里的案例的前提是在【0，1】的区间f(x)=x^3−x 是收敛的 

>> max=0.000000;
phi=10^(-4); %收敛的精度
step=0.0001;   %设置迭代的步长
for i=0:step:1		%将区间按0.0001分割
    x1=i;			%初值大小
    newton=@(x)x - (x^3/3-x)/(x^2-1);%f(x)=x^3/3-x内部函数
	f_1=@(x)3*x-1; % 计算是否存在2阶导数
	 mm=f_1(x1);
	if  mm==0
	break;
	end;
    k=0;
	err=1.000;%允许误差大小
    while(err>phi)
        x2=newton(x1); % 计算牛顿
        err=abs(x2-x1);
        x1=x2;
        k=k+1;
        %fprintf('%d  %1.15d   %1.15f\n',k,x1,err);
        if x1==0
            max=i;        %记录的最大值
        end
    end
end
fprintf('max= %1.15f\n',max)
max= 0.774300000000000
>>