本文以 Java 语言实现，整理的代码模板适用于编程竞赛。对代码模板原理的讲解不多，主要记录一下如何使用。

目录

一、算法模板：整数二分

二、例题

---

一、算法模板：整数二分

整数二分有两套算法模板，这两套算法模板几乎涵盖了所有二分算法的题目。

它们的主要区别在于①和②处 对 mid 的赋值不同，相应的，右边界 r 与左边界 l 的值的更新也就不同。整数二分的本质在于边界的判断。每次都必须选择答案所在的区间进行处理。

在运用下面两套模板时，先不要管细节；找到题干中要求的性质的边界后，先套上模板即可；然后再对边界点作出考虑：如果 check() 的值为 true，边界点包括不包括在目标区间内？根据这个问题的结果，填充：

if(check()) {
    ...    //填充
}else{
    ...    //填充
}

再根据实际填充的结果，对应到下面的模板，确定 mid 的赋值处是否要加一。 

// 检查x是否满足某种性质
boolean check(int x) {
    ...
}


// 模板一：当区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用
int bsearch_1(int l, int r) {
    while (l < r) {
        int mid = (l + r) >> 1;    //①

        if (check(mid)) {
            r = mid; // check()判断mid是否满足性质
        } else {
            l = mid + 1;
        }

        return l;
}

// 模板二：当区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用
int bsearch_2(int l, int r) {
    while (l < r) {
        int mid = (l + r + 1) >> 1;    //②

        if (check(mid)) { 
            l = mid;
        } else { 
            r = mid - 1;
        }
        
        return l;
}

---

二、例题

例题：acwing-789.数的范围

解析：

这道题直接暴力是会超时的，最好的方法就是二分求解。

如果要查找起始点：

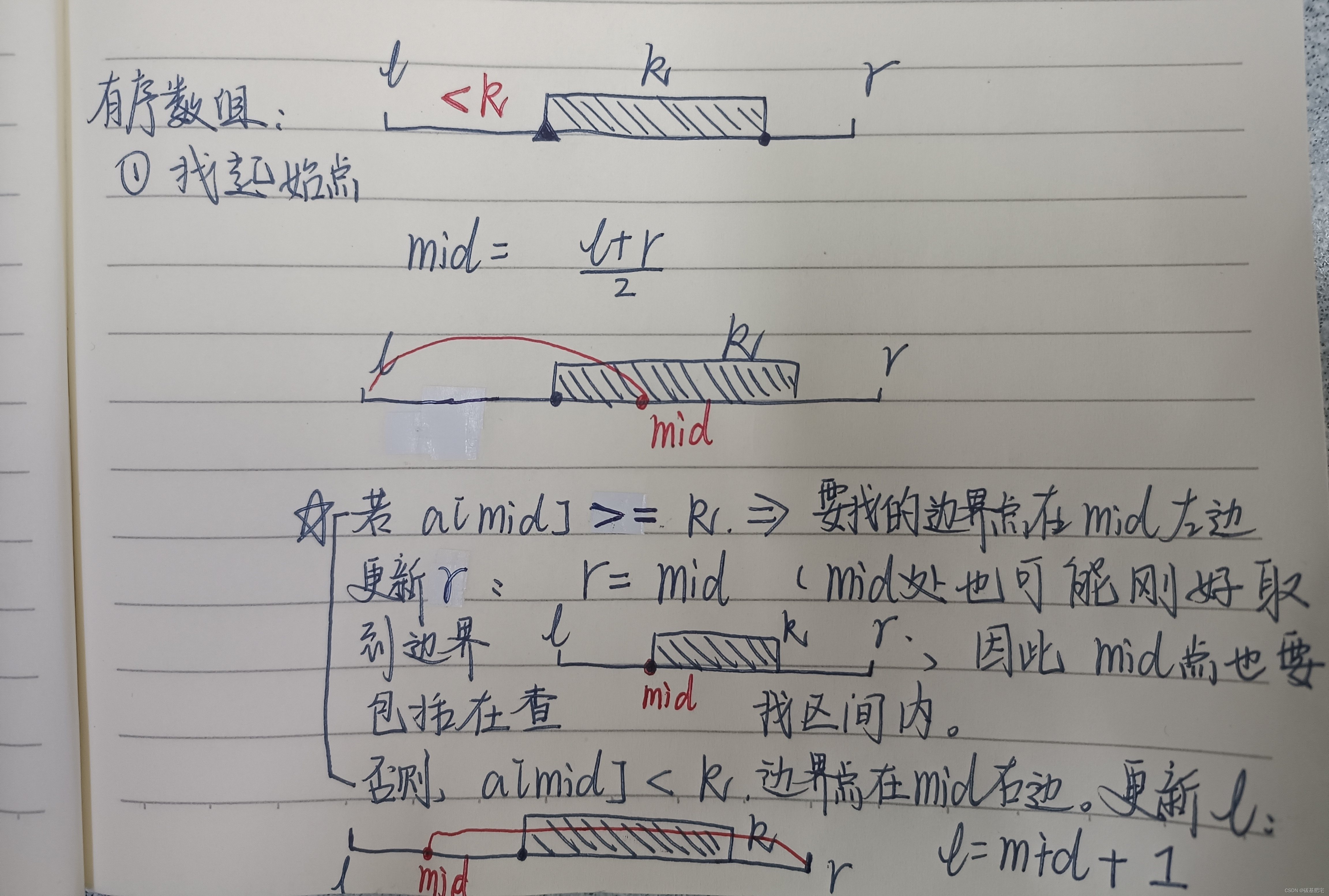由上面的分析过程和代码模板可得如下代码：

// 二分找开始点
int l = 0, r = n-1;
while(l < r) {
    int mid = (l+r) >> 1;

    if(array[mid] >= k) {
        r = mid;
    }else{
        l = mid + 1;
    }
}

因为下面的步骤是 r = mid 和 l = mid + 1，所以， mid 的赋值即为 (l+r) >> 1，不用再更改为  (l+r+1) >> 1 。

然后二分查找终点：

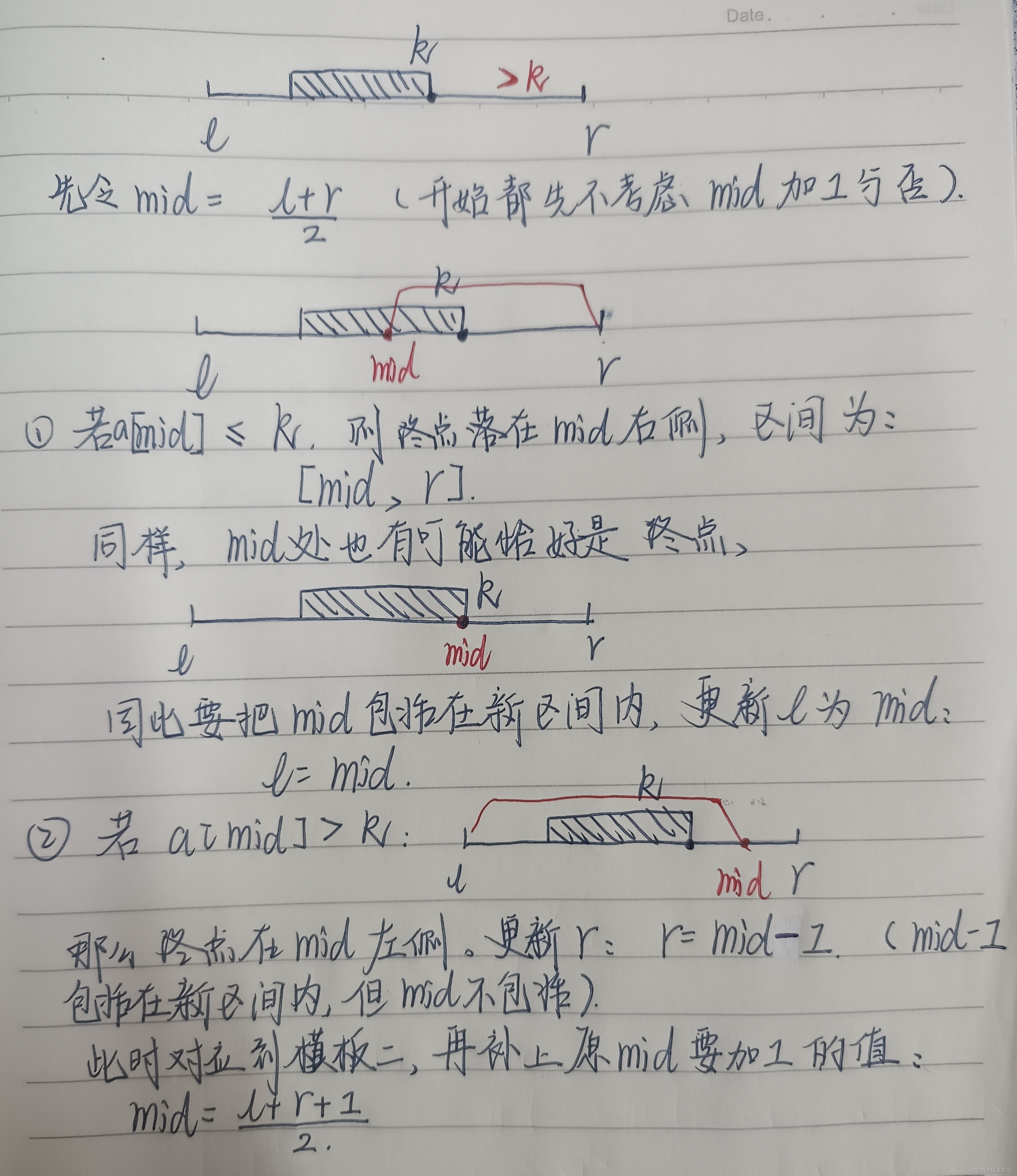
因此，得出查找终点的代码如下：

// 二分找结束点
l = 0;
r = n-1;
while(l < r) {
    int mid = (l+r+1) >> 1;

    if(array[mid] <= k) {
        l = mid;
    }else{
        r = mid - 1;
    }
}

题干可能不一定有解，但是二分的模板是一定有解的。二分后，通过性质，我们可以自行判断出无解的情况是什么。本题中，二分代码结束后 l 于 r 一定是相等的。此时，若 k 不等于 array[l]，那么说明要查找的数不存在。 

结合题干要求的输入输出格式，补充完整代码：

import java.util.Scanner;


public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int n = reader.nextInt();   //数组长度
        int q = reader.nextInt();   //询问个数
        int[] array = new int[n];
        for (int i = 0; i < array.length; i++) {
            array[i] = reader.nextInt();
        }

        while(q != 0) {
            q--;
            int k = reader.nextInt();   //要查询的元素

            // 二分找开始点
            int l = 0, r = n-1;
            while(l < r) {
                int mid = (l+r) >> 1;

                if(array[mid] >= k) {
                    r = mid;
                }else{
                    l = mid + 1;
                }
            }
            //没找到
            if(array[l] != k) {
                System.out.println("-1 -1");
            }else {
                System.out.print(l + " ");
                // 二分找结束点
                l = 0;
                r = n-1;
                while(l < r) {
                    int mid = (l+r+1) >> 1;

                    if(array[mid] <= k) {
                        l = mid;
                    }else{
                        r = mid - 1;
                    }
                }
                System.out.println(l);

            }
        }
        reader.close();
    }
}