二进制码与格雷码的相互转换原理与Verilog实现
- 一、写在前面
- 二、二进制码与格雷码的相互转换
- 2.1 二进制码转格雷码原理
- 2.2 异或运算的特性
- 2.3 格雷码转二进制码原理
- 三、二进制码与格雷码相互转换的Verilog实现
- 四、仿真验证
- 五、写在后面
一、写在前面
二进制码是一种基于二进制数系统的编码方式,使用 0 和 1 两个数字来表示数字信号。例如,数字 7 在二进制码中表示为0111。
而格雷码是一种二进制反射码,也称为格雷反码。格雷码中的相邻两个码位只有一个位的变化,可以减少数字信号传输过程中的传输错误率。例如,数字 7 在格雷码中表示为 0100。
在数字电路中,格雷码的编码方式可以大大简化电路的设计。由于相邻两个码位只有一个位的变化,因此在使用格雷码编码时,只需要使用异或门就可以实现数字信号的编码和解码。而使用二进制码进行编码时,需要使用更多的逻辑门才能实现编码和解码。
二、二进制码与格雷码的相互转换
2.1 二进制码转格雷码原理
假设n比特的二进制码为
B
n
−
1
B
n
−
2
.
.
.
B
1
B
0
B_{n-1}B_{n-2}...B_1B_0
Bn−1Bn−2...B1B0,而转换后的n比特格雷码为
G
n
−
1
G
n
−
2
.
.
.
G
1
G
0
G_{n-1}G_{n-2}...G_1G_0
Gn−1Gn−2...G1G0,二进制码转格雷码的法则如下:格雷码的最高位等于二进制码的最高位,而格雷码得次高位等于二进制码的最高位与二进制码次高位的异或结果,格雷码的其他位与次高位的求法相类似。
G
n
−
1
=
B
n
−
1
G
i
=
B
i
+
1
⊕
B
i
\begin{matrix} G_{n-1}=B_{n-1} \\ \\G_{i}=B_{i+1}\oplus B_{i} \end{matrix}
Gn−1=Bn−1Gi=Bi+1⊕Bi
以4比特的二进制码转格雷码为例,如下图所示。

2.2 异或运算的特性
在《数字电子技术基础》中,我们学过异或运算,异或运算有一点特性很重要。如果 A ⊕ B = C A \oplus B=C A⊕B=C,则 A ⊕ C = B A \oplus C=B A⊕C=B, B ⊕ C = A B \oplus C=A B⊕C=A,如下图所示。

2.3 格雷码转二进制码原理
那么,根据异或运算的特性,我们可以对二进制转格雷码的法则进行变化,得到格雷码转二进制的公式,如下:
B
n
−
1
=
G
n
−
1
B
i
=
B
i
+
1
⊕
G
i
\begin{matrix} B_{n-1}=G_{n-1} \\ \\B_{i}=B_{i+1}\oplus G_{i} \end{matrix}
Bn−1=Gn−1Bi=Bi+1⊕Gi
即二进制码的最高位等于格雷码的最高位,而二进制码的次高位等于二进制码的最高位与格雷码的次高位异或结果。而二进制码的其他位与二进制码的次高位求法相似。
以4比特的格雷码转二进制码为例,如下图所示。

三、二进制码与格雷码相互转换的Verilog实现
根据上述的二进制码转格雷码与格雷码转二进制码的原理,可以编写Verilog代码,如下。
module BinaryGrayConvert
#(
parameter DATA_WIDTH = 8 //二进制码/格雷码位宽
)
(
input [DATA_WIDTH-1:0] binary_in , //二进制码输入
input [DATA_WIDTH-1:0] gray_in , //格雷码输入
output [DATA_WIDTH-1:0] binary_out, //二进制码输出
output [DATA_WIDTH-1:0] gray_out //格雷码输出
);
//二进制码转格雷码
assign gray_out = binary_in ^ (binary_in>>1);
//格雷码转二进制码
genvar i;
generate
for(i=0;i<DATA_WIDTH;i=i+1) begin:gray2binary
if(i==DATA_WIDTH-1)
assign binary_out[i] = gray_in[i];
else
assign binary_out[i] = binary_out[i+1] ^ gray_in[i];
end
endgenerate
endmodule
四、仿真验证
对该二进制码与格雷码的相互转换模块编写TestBench进行仿真。
`timescale 1ns/1ns //时间单位/精度
module tb_BinaryGrayConvert();
parameter DATA_WIDTH = 8;
reg clk,rst_n;
reg [DATA_WIDTH-1:0] binary_in ; //二进制码输入
reg [DATA_WIDTH-1:0] gray_in ; //格雷码输入
wire [DATA_WIDTH-1:0] binary_out; //二进制码输出
wire [DATA_WIDTH-1:0] gray_out ; //格雷码输出
initial begin
clk = 1'b0;
rst_n <= 1'b0;
#20
rst_n <= 1'b1;
end
always #10 clk = ~clk;
always @(posedge clk or negedge rst_n)
if(!rst_n) begin
binary_in <= 8'b0000_0000;
gray_in <= 8'b0000_0000;
end
else begin
binary_in <= binary_in + 1'b1;
gray_in <= gray_in + 1'b1;
end
BinaryGrayConvert
#(
.DATA_WIDTH(DATA_WIDTH) //二进制码/格雷码位宽
)
BinaryGrayConvert_inst
(
.binary_in (binary_in ), //二进制码输入
.gray_in (gray_in ), //格雷码输入
.binary_out(binary_out), //二进制码输出
.gray_out (gray_out ) //格雷码输出
);
endmodule
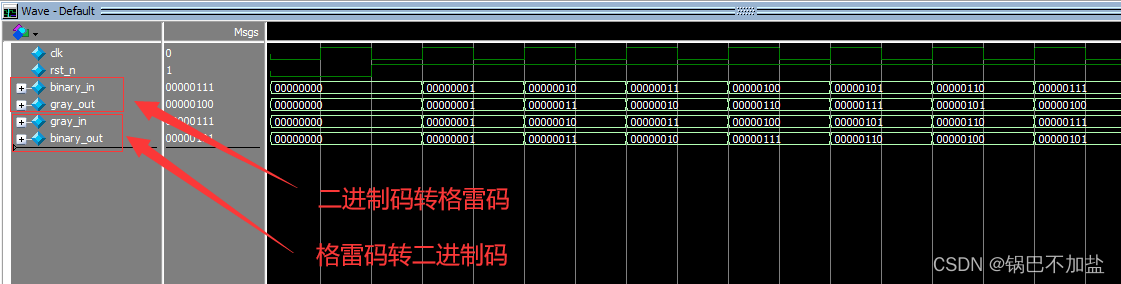
仿真结果如下图所示,观察波形,以 ( 00000101 ) B i n a r y − > ( 00000111 ) G r a y (00000101)_{Binary} -> (00000111)_{Gray} (00000101)Binary−>(00000111)Gray, ( 00000101 ) G r a y − > ( 00000110 ) B i n a r y (00000101)_{Gray} -> (00000110)_{Binary} (00000101)Gray−>(00000110)Binary为例,可见转换正确,符合我们预期实现的二进制码与格雷码的相互转换。
五、写在后面
在本文中,我们学习了二进制码与格雷码相互转换的原理,并使用Verilog实现,同时编写TestBench文件对其进行仿真,验证模块的正确性。如果有疑义的地方欢迎评论区友好探讨学习!!!!!









![[排序算法]桶排序](https://img-blog.csdnimg.cn/bb395a3a10ea4de8ac4b3850a2950113.png)