目录

1、实验目的：

2、实验内容：

---

1、实验目的：

1）掌握定义符号对象和创建符号表达式的方法；

2）掌握符号运算基本命令和规则；

3）掌握符号表达式的运算法则以及符号矩阵运算；

4）掌握符号微积分和符号方程求解的基本方法。

2、实验内容：

2-1）、分别用sym和syms创建符号表达式： 

 

 

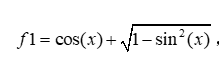
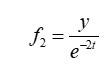
syms x ;
f1 = cos(x)+sqrt((1-sin(x)^2))
syms y t;
f2 = y / exp(-2*t)

输出结果 

 

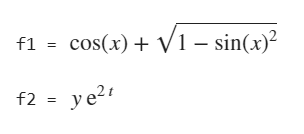
2-2）、求表达式？在x=1.723处的，精度为20位的代数值。

syms x y;
x = 1.723;
y = (3*x^3 + x^2 - 1) / (x^2 + 1);
vpa(subs(y, x, 1.723), 20) %求x=1.723处值，精度为20位

2-3）、求下列级数之和（提示：利用symsum(s,v,n,m)函数实现）

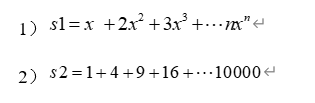
syms x n;
s1 = n*x^n
symsum(s1, n, 1, inf)

syms x;
s2 = x^2
symsum(s2, x, 1, 100)

第二小问可以用for循环验证答案

% 用for循环验证
sum = 0;
for j = (1:100)
        sum = sum + j^2;
end
sum %验证结果正确

 两次输出结果都=338350，没问题~

2-4）、计算下列极限值：

 

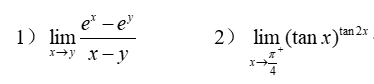
syms x y;
fx = (exp(x) - exp(y)) / (x - y);
lim1 = limit(fx, x, y)

clear
syms x;
fx = tan(x)^(tan(2*x));  %输入表达式
lim2 = limit(fx, x, pi/4, 'right') %趋近于π/4(+)，求极限

2-5）、求复合函数；

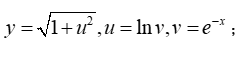
暂时不会用compose函数

 

 

2-6）、

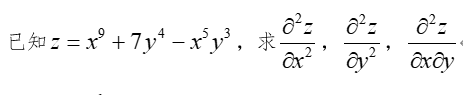
syms x y;
z = x^9 + 7*y^4-x^5*y^3
diff(z, 'x', 2) %对z符号表达式的x变量 求二阶导数
diff(z, 'y', 2) %y的二阶偏导数
diff(diff(z, 'x', 1),'y',1) % xy的偏导数

2-7）、求方程组的解。

 

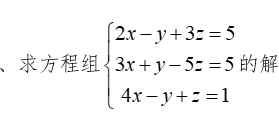
clear
syms x y z;
a = [2*x-y+3*z == 5, 3*x+y-5*z == 5, 4*x-y+z == 1];
b= [x y z];
S = solve(a, b)

2-8）、分别计算下列表达式

syms x;
y1 = x^4/(1+x^2);
i1 = int(y1)         %不定积分
y2 = 3*x^2-x+1;
i2 = int(y2, 2, 0)   %对y2积分，上限2，下限0

2-9）、求解当y(0)=2，z(0)=7时，微分方程组的解

 

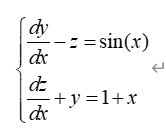
syms x y z;
[y,z]=dsolve('Dy-z=sin(x)','Dz+y=1+x','y(0)=2','z(0)=7','x')