前言

当前所有算法都使用测试用例运行过，但是不保证100%的测试用例，如果存在问题务必联系批评指正~

在此感谢左大神让我对算法有了新的感悟认识！

问题介绍

原问题
给定三个点坐标代表三角形的三个顶点，再给定一个（x,y）点，判断该点是否在三角形内部

解决方案

原问题：
方法一：面积法
1、利用海伦公式求出以改点为顶点，三角形各边为底边的三角形面积之和，如果该和大于三角形的总面积，那么点在外面，如果不大于，则点在里面
优点：容易想到，容易编写，只需要编写点到点之间的距离即可利用公式快速计算面积从而判断答案
缺点：由于海伦公式存在开根会导致精度缺失判断失误
方法二：向量法
如下图：
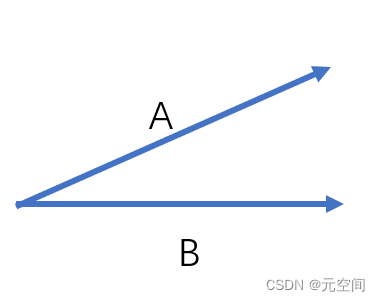
在这里插入图片描述
1、向量的叉乘，假设A(2,1) B(2,0)，则AxB = 0-2 = -2 < 0 ,也就是说如果A向量旋转到B向量同向时，叉乘为负数，反之则为正数
2、由此可以得到一个点在向量的那一侧，如果在右侧，那么叉乘为负数，如果在左侧，那么叉乘为正数
3、为什么要这个准备工作呢？我们再看一张图：
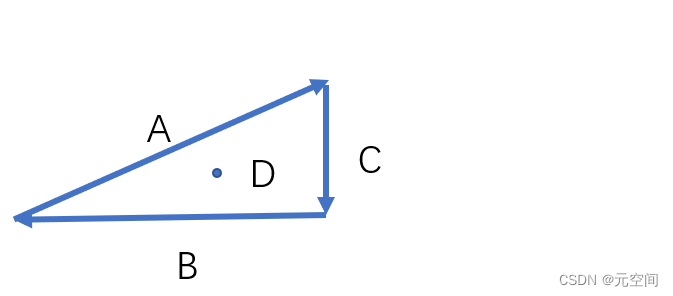
在这里插入图片描述

4、如果D点在三角形内，那么我们就能够得到D点一定在ABC三条边的同一侧！
5、所以更具这个定理我们只需要写一个叉乘的方法就能够解决
优点：简单快捷、没有精度缺失问题
缺点：不容易想到，容易被方法一抢风头~

代码编写

java语言版本

原问题：
方法一:

   /**
     * 二轮测试：判断点是否在三角形的内部
     * 方法一：面积法
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @param x3
     * @param y3
     * @param x
     * @param y
     * @return
     */
    public static boolean isInsideCp1(double x1, double y1,
                                      double x2, double y2,
                                      double x3, double y3,
                                      double x, double y) {
        return getSquare(x1, y1, x2, y2, x, y) + getSquare(x1, y1, x3, y3, x, y) + getSquare(x3, y3, x2, y2, x, y)
                <= getSquare(x1, y1, x2, y2, x3, y3);
    }

    /**
     * 给定三个点，求三角形面积
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @param x3
     * @param y3
     * @return
     */
    private static double getSquare(double x1, double y1,
                                    double x2, double y2,
                                    double x3, double y3) {
        // 先求三边
        double len1 = getLen(x1, y1, x2, y2);
        double len2 = getLen(x1, y1, x3, y3);
        double len3 = getLen(x2, y2, x3, y3);
        double p = (len1 + len2 + len3)/2;
        return Math.sqrt(p * (p-len1) * (p - len2) * (p - len3));
    }

    /**
     * 计算两点之间的距离
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @return
     */
    private static double getLen(double x1, double y1,
                                 double x2, double y2) {
        return Math.sqrt((x1-x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
    }

方法二：

    /**
     * 二轮测试：判断点是否在三角形内
     * 方法二：向量法
     * 该方法不存在精度问题导致的结果不准确
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @param x3
     * @param y3
     * @param x
     * @param y
     * @return
     */
    public static boolean isInsideCp2(double x1, double y1,
                                      double x2, double y2,
                                      double x3, double y3,
                                      double x, double y) {
        // 判断点是否是顺时针顺序，如果不是则调整一下
        if (getCrossCp2(x1, y1, x3, y3, x2, y2) < 0) {
            // 说明x2，y2在右边,交换3和2
            double temx = x2;
            double temy = y2;
            x2 = x3;
            y2 = y3;
            x3 = temx;
            y3 = temy;
        }
        // 判断叉乘是否都是小于0
        if (getCrossCp2(x1, y1, x2, y2, x, y) <= 0
                && getCrossCp2(x2, y2, x3, y3, x, y) <= 0
                && getCrossCp2(x3, y3, x1, y1, x, y) <= 0) {
            return true;
        }
        return false;
    }


    /**
     * 计算x，y点在(x1, y2) -> (x2, y2) 向量的左边还是右边
     * 大于0，左边 小于0，右边
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @param x
     * @param y
     * @return
     */
    public static double getCrossCp2(double x1, double y1,
                                     double x2, double y2,
                                     double x, double y) {
        // 以x1，y1为基准
        double xs = x2 - x1;
        double ys = y2 - y1;
        double xs1 = x - x1;
        double ys1 = y - y1;
        // 计算叉乘
        return xs * ys1 - ys * xs1;
    }





    public static void main(String[] args) {
        System.out.println(isInsideCp2(0 ,0, 2, 0, 1, 2, 1, 1));
    }