创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!!
主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步!
给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ
c语言系列专栏: c语言之路重点知识整合
文章相关知识点:c语言指针详解
目录
一、 函数名的本质
二、如何定义函数指针
总结定义函数指针的过程:
三、函数指针的利用
四、函数指针数组
一、 函数名的本质
我们定义一个函数,然后输出函数名查看一下:
#include <stdio.h>
int add_int(int a,int b);
int main()
{
printf("%d\n", add_int);
return 0;
}
int add_int(int a,int b)
{
int sum=0;
sum=a+b;
return sum;
} 输出结果为一个地址:
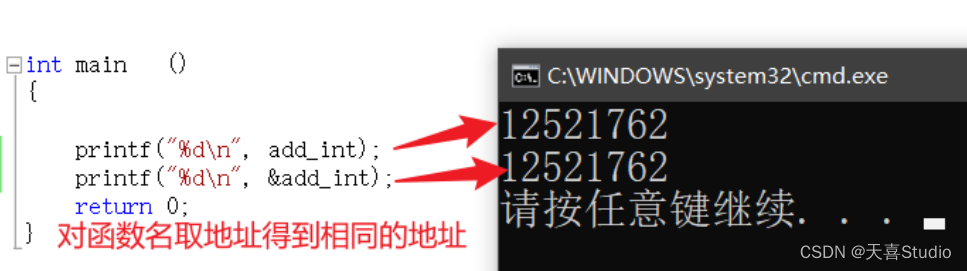
函数名字的本质: 代表函数在内存中的地址
使用调试器查看: C_3_1.exe中的add_int函数 地址为0x00801d50

函数名就是地址!!!
既然函数名是地址,就可以用指针变量来保存,就需要函数指针的概念。
二、如何定义函数指针
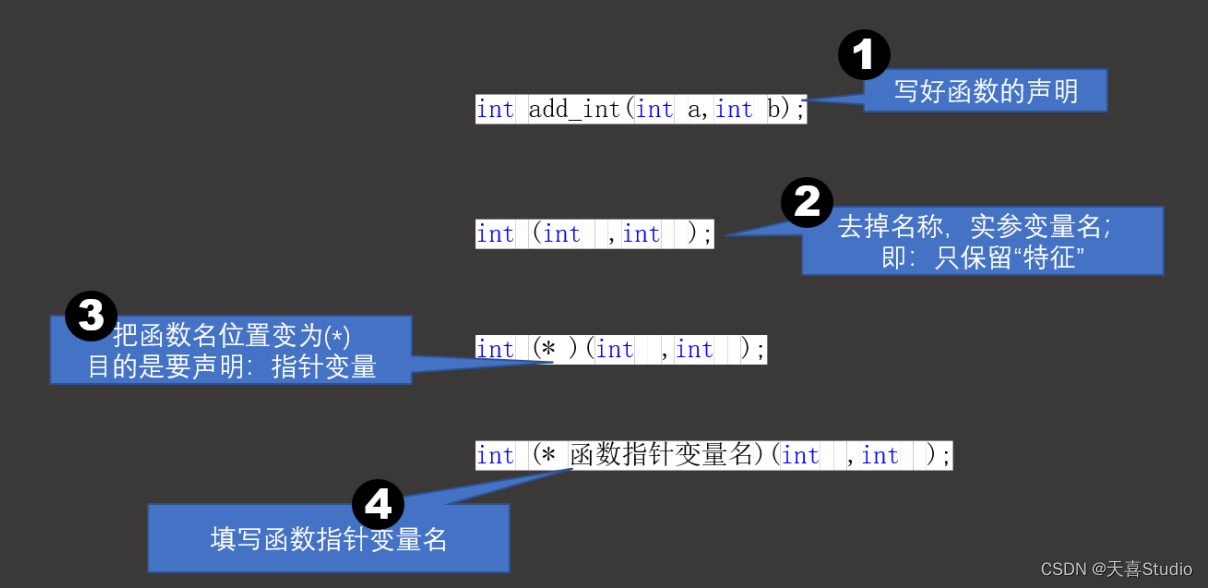
根据指针的使用经验: 指针变量必须强调是什么类型的指针。因此,函数的指针定义时必须把函数的特征表述清楚。
数组的特征:int [ ]
把函数名去掉就是函数的特征:int (int a, int b)
数组指针:把数组名替换成指针 再加上数组的特征 int(*parr)[5];
类比数组指针 函数指针类型:int(* )(int a, int b); 再加上函数指针的名就是函数指针:
int (*pfun)(int ,int ); //声明一个能指向add_int的函数指针
pfun=add_int; //方式1:把函数名赋给函数指针变量
pfun=&add_int; //方式2:把函数名先取地址,再把计算的地址赋给函数指针变量使用调试器查看:

pfun为函数指针类型,指向了C_3_1.exe中的add_int函数。
总结定义函数指针的过程:
三、函数指针的利用
利用函数指针执行函数代码
两种方式:显式: (*函数指针)(实际参数) 隐式: 函数指针(实际参数)
#include <stdio.h>
#include <math.h>
int add_int(int a,int b);
int main()
{
int(*pfun)(int a, int b)=&add_int; //为函数指针赋值,使其能指向函数代码,并能执行所指向的函数代码 把函数名先取地址,再把计算的地址赋给函数指针变量
printf("%d\n", (*pfun)(8, 9)); //显式的使用,让人一目了然它是一个函数指针
//int(*pfun)(int a, int b)=add_int; //把函数名赋给函数指针变量
printf("%d\n", pfun(8, 9) ); //隐式的使用,让人看不出它是否是函数指针,字面上与下行代码无异
printf("%d\n",add_int(111,222));//通过函数名调用函数
/* 定义指向函数的指针变量 就可以调用内存中的函数代码 */
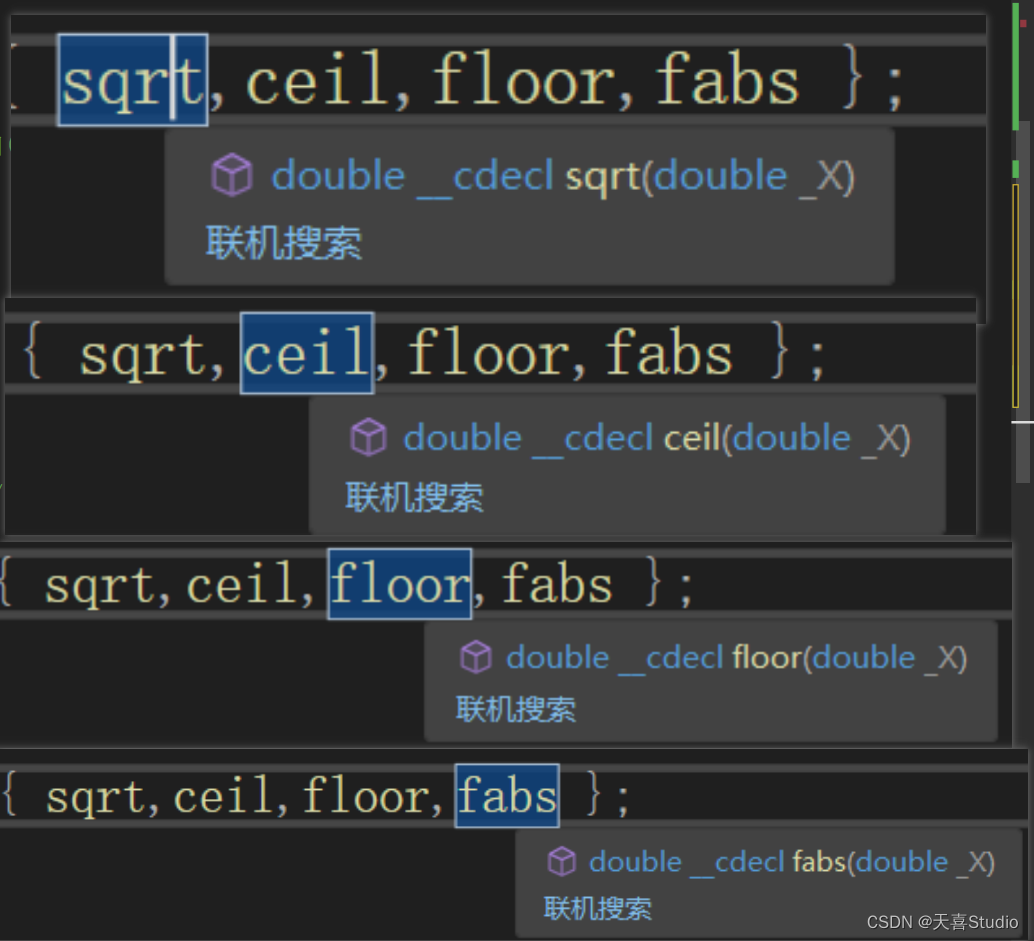
// sqrt() ceil() floor() fabs()
double (*pmath)(double);
pmath = sqrt;
printf("%f\n", pmath(2));
return 0;
}
int add_int(int a,int b)
{
int sum=0;
sum=a+b;
return sum;
}
定义指向函数的指针变量 就可以调用内存中的函数代码
四、函数指针数组
类比指针数组,同特征不同函数名的函数,可以定义函数指针数组
#include <stdio.h>
#include <math.h>
int add_int(int a,int b);
int main()
{
double (*pmaths[4])(double) = { sqrt,ceil,floor,fabs };
for (int i = 0; i < 4; i++)
{
printf("%f\n", pmaths[i](2.5));
}
return 0;
}
int add_int(int a,int b)
{
int sum=0;
sum=a+b;
return sum;
}
调试器查看:pmaths为函数指针数组 ,存放的都是函数指针