目录
- 一、DE
- 1.步骤
- 2.特点
- 二、DE Optimiza
- 1.函数最小值问题
- 2.差分进化算法求解
- 2.Java 实现与结果绘图
一、DE
差分进化算法是一种基于群体智能的优化算法,由Storn和Price于1995年提出,最早用来解决切比雪夫多项式问题。它采用实数编码方式,通过变异、交叉和选择等操作,使种群逐渐向全局最优解收敛。
1.步骤
差分进化算法的主要步骤如下:
- 初始化参数:设定种群规模
NP,变异因子F,交叉概率CR,个体维度D,决策空间上下界Xu和Xl,终止条件等。 - 初始化种群:在决策空间内随机生成NP个D维的个体作为初始种群X。
- 种群变异:对每个个体X(i),随机选择三个不同的个体X(r1),X(r2),X(r3),并计算变异向量 V ( i ) = X ( r 1 ) + F ∗ ( X ( r 2 ) − X ( r 3 ) ) V(i) = X(r_1) + F * (X(r_2) - X(r_3)) V(i)=X(r1)+F∗(X(r2)−X(r3))。
- 种群交叉:对每个个体X(i)和变异向量V(i),按照交叉概率
CR进行交叉操作,生成向量 U(i)。交叉操作的方法有多种,一种常用的方法是二项式交叉,即对每个维度 j,如果 rand(j) <= CR 或者 j == jrand(jrand为随机选定的一个维度),则 U ( i , j ) = V ( i , j ) U(i,j) = V(i,j) U(i,j)=V(i,j),否则 U ( i , j ) = X ( i , j ) U(i,j) = X(i,j) U(i,j)=X(i,j)。 - 最优种群选择:对每个个体 X(i) 和向量 U(i),根据目标函数值的大小进行最优选择,即如果 f ( U ( i ) ) < = f ( X ( i ) ) f(U(i)) <= f(X(i)) f(U(i))<=f(X(i)),则保留 U(i) 作为下一代的个体,否则保留 X(i)。
- 边界条件处理:对每个个体,检查其是否超出决策空间的边界,如果是,则进行相应的处理。处理方法有多种,一种常用的方法是边界吸收,即将超出边界的分量设置为边界值。
- 终止条件判断:判断是否达到终止条件,如最大迭代次数、目标函数值阈值等。如果是,则停止迭代并输出最优解;如果否,则返回第三步继续迭代。
差分进化算法具有结构简单、性能优越、自适应性强、并行性好等特点。它可以用来求解多种类型的优化问题,如单目标优化、多目标优化、约束优化、大规模优化等。它也可以与其他算法结合或进行改进,以提高其效率和鲁棒性。
2.特点
差分进化算法的优点有:
- 结构简单,只需要调整三个参数(F,CR,NP),易于实现和使用。
- 性能优越,具有较快的收敛速度和较高的精度,能够解决复杂的非线性、非凸、多峰的优化问题。
- 自适应性强,能够根据问题特征和进化过程动态调整变异因子和交叉概率,提高搜索效率和鲁棒性。
- 并行性好,能够利用多核处理器或分布式计算平台进行并行计算,加速优化过程。
差分进化算法的缺点有:
- 参数选择依赖于问题特征和经验,没有统一的理论指导,可能影响算法的性能和稳定性。
- 对于高维、大规模、多约束的优化问题,可能出现收敛速度慢、陷入局部最优、多样性丢失等问题。
- 对于离散、整数、混合编码等类型的优化问题,需要进行特殊的编码和解码处理,增加了算法的复杂度。
差分进化算法和其他优化算法的区别主要有以下几点:
- 差分进化算法采用实数编码,而其他优化算法如遗传算法、粒子群优化算法等可能采用二进制编码或混合编码。
- 差分进化算法的变异操作是利用种群中个体的差向量作为扰动源,而其他优化算法的变异操作可能是随机改变个体的某些分量或基因。
- 差分进化算法的交叉操作是按照交叉概率进行参数混合,而其他优化算法的交叉操作可能是按照某种规则进行基因重组或交换。
- 差分进化算法的选择操作是贪婪选择,即试验向量只与目标向量进行比较和替换,而其他优化算法的选择操作可能是轮盘赌选择、锦标赛选择等,即根据适应度值决定个体被选择的概率。
- 差分进化算法的参数设置相对简单,只需要调整三个参数(F,CR,NP),而其他优化算法的参数设置可能更复杂或依赖于问题特征。
二、DE Optimiza
1.函数最小值问题
假设我们要求解以下函数的最小值:
f ( x , y ) = sin ( x ∗ x + y ∗ y ) / ( x ∗ x + y ∗ y + 1 ) f(x,y)=\sin(x * x + y * y) / (x * x + y * y + 1) f(x,y)=sin(x∗x+y∗y)/(x∗x+y∗y+1)
其中, x , y ∈ [ − 5 , 5 ] x,y\in[-5,5] x,y∈[−5,5]。
通过函数绘图工具得出函数分布情况,存在多处的呈现环形分布的局部最小:

2.差分进化算法求解
- 初始化参数:设定种群规模 NP=100,变异因子 F=0.5,交叉概率 CR=0.1,个体维度 D=2,决策空间上下界 [-5,5],终止条件为最大迭代次数 maxGen=100 或目标函数值小于阈值 e p s = 1 0 − 8 eps=10^{-8} eps=10−8。
- 初始化种群:在决策空间内随机生成 NP 个 D 维的个体作为初始种群 X,并计算它们的目标函数值 f i t fit fit。
- 种群变异:对每个个体 X(i),随机选择三个不同的个体 X(r1),X(r2),X(r3) 进行变异操作 → V(i)。
- 种群交叉:对每个个体 X(i)和变异向量 V(i),按照交叉概率CR进行交叉操作 → U(i)。
- 最优种群选择:对每个个体X(i)和新个体 U(i),根据目标函数值的大小进行选择。
- 边界条件处理。
- 终止条件判断:判断是否达到终止条件,如果是,则停止迭代并输出最优解;否则返回第三步继续迭代。
2.Java 实现与结果绘图
这里添加使用 StdDraw 库进行绘图。图形库下载
- 简单介绍
1.设置 x、y 坐标轴
StdDraw.setXscale(a, b);
StdDraw.setYscale(c, d);
2.清空画布
StdDraw.clear();
3.设置粗细、颜色
StdDraw.setPenRadius(0.001);
StdDraw.setPenColor(StdDraw.BLACK);
4.绘制线条、正方形、长方形、点、圆
StdDraw.line(a, 0, b, 0);
StdDraw.square(0, 0, 1);
StdDraw.rectangle(0,0,1,2)//中点 (0,0),中点宽度、长度延伸
StdDraw.point(a, b);
StdDraw.circle(0, 0, r);
2.code
package code;
//Differential Optimization
import edu.princeton.cs.algs4.StdDraw;
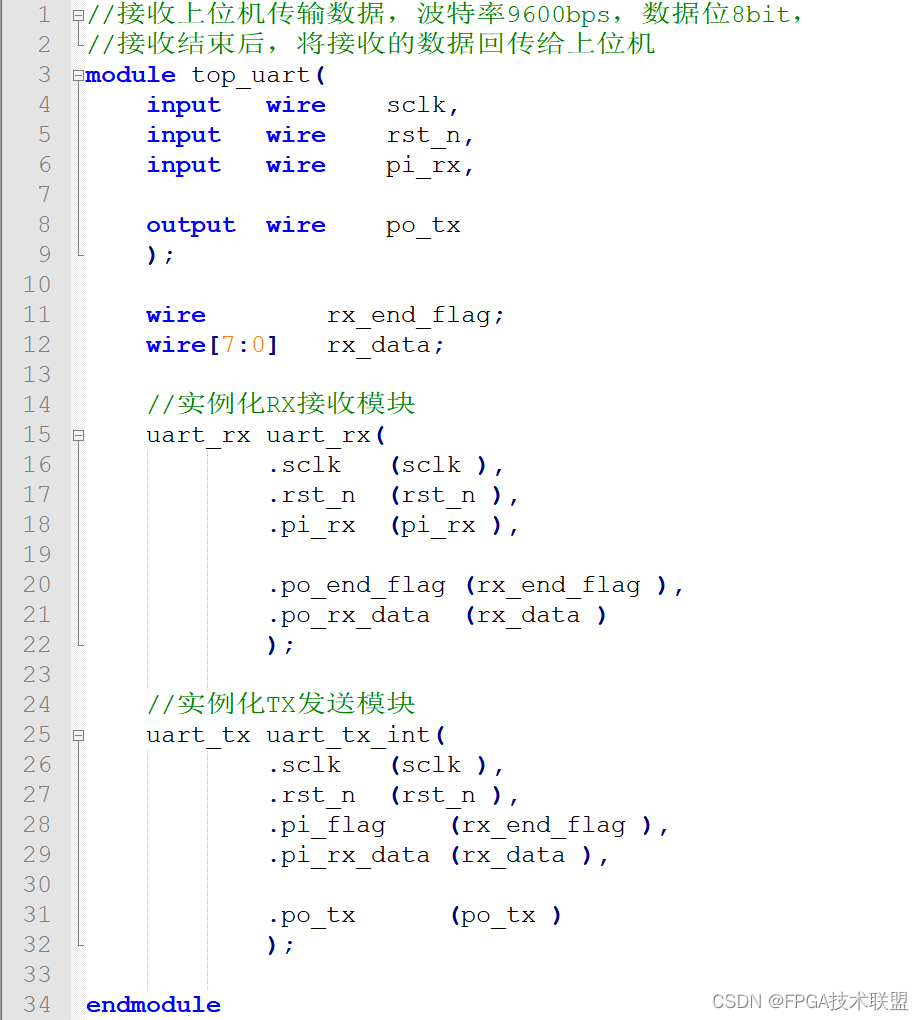
public class c0_DEjava {
//static int n = 100; // 离散化步数
static double a = -5, b = 5, c = -5, d = 5; // 取值范围
static double f(double x, double y) { // 待优化的函数
return Math.sin(x * x + y * y) / (x * x + y * y + 1);
}
static int popSize = 100; // 种群大小
static double F = 0.5, CR = 0.1; // 差分进化算法参数0.5
static int maxGen = 100; // 最大迭代次数
static double eps = 1e-8; // 终止条件
static double[][] pop = new double[popSize][2]; // 种群
static double[] fit = new double[popSize]; // 种群适应度
static double[] best = new double[2]; // 最优解
static double bestFit; // 最优解的适应度
public static void main(String[] args) {
// 初始化种群
for (int i = 0; i < popSize; i++) {
pop[i][0] = a + (b - a) * Math.random();
pop[i][1] = c + (d - c) * Math.random();
}
// 迭代
for (int gen = 1; gen <= maxGen; gen++) {
// 计算种群适应度
for (int i = 0; i < popSize; i++) {
fit[i] = f(pop[i][0], pop[i][1]);
}
// 找出最优解
int bestIndex = 0;
for (int i = 1; i < popSize; i++) {
if (fit[i] < fit[bestIndex]) {
bestIndex = i;
}
}
best[0] = pop[bestIndex][0];
best[1] = pop[bestIndex][1];
bestFit = fit[bestIndex];
System.out.println(gen+" fit="+bestFit+": x="+best[0]+",y="+best[1]);
StdDraw.setXscale(a, b);
StdDraw.setYscale(c, d);
// 更新种群
for (int i = 0; i < popSize; i++) {
double[] trial = new double[2];
// 差分操作
int r1, r2, r3;
do {
r1 = (int) (Math.random() * popSize);
} while (r1 == i);
do {
r2 = (int) (Math.random() * popSize);
} while (r2 == i || r2 == r1);
do {
r3 = (int) (Math.random() * popSize);
} while (r3 == i || r3 == r1 || r3 == r2);
for (int j = 0; j < 2; j++) {
trial[j] = pop[r1][j] + F * (pop[r2][j] - pop[r3][j]);
}
// 交叉操作
int jrand = (int) (Math.random() * 2);
for (int j = 0; j < 2; j++) {
if (Math.random() < CR || j == jrand) {
trial[j] = Math.max(a, Math.min(b, trial[j]));
} else {
trial[j] = pop[i][j];
}
}
// 选择操作
double trialFit = f(trial[0], trial[1]);
if (trialFit < fit[i]) {
pop[i][0] = trial[0];
pop[i][1] = trial[1];
fit[i] = trialFit;
}
}
// 绘制迭代过程
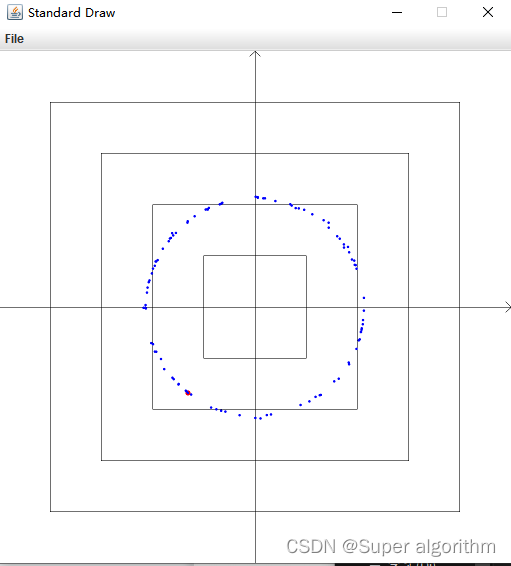
if (gen>0 ){
StdDraw.clear();
StdDraw.setXscale(a, b);
StdDraw.setYscale(c, d);
StdDraw.setPenRadius(0.001);
StdDraw.setPenColor(StdDraw.BLACK);
StdDraw.line(a, 0, b, 0);//x
StdDraw.line(b-0.1, 0.1, b, 0);
StdDraw.line(b-0.1, -0.1, b, 0);
StdDraw.line(0, a, 0, b);//y
StdDraw.line(0.1, b-0.1, 0, b);
StdDraw.line(-0.1, b-0.1, 0, b);
StdDraw.square(0, 0, 1);
StdDraw.square(0, 0, 2);
StdDraw.square(0, 0, 3);
StdDraw.square(0, 0, 4);
StdDraw.setPenRadius(0.01);
StdDraw.setPenColor(StdDraw.RED);
StdDraw.point(best[0], best[1]);
StdDraw.setPenRadius(0.005);
StdDraw.setPenColor(StdDraw.BLUE);
for (int i = 0; i < popSize; i++) {
StdDraw.point(pop[i][0], pop[i][1]);
}
}
// 判断终止条件
if (bestFit < eps) {
// break;
}
}
}
}

☕物有本末,事有终始,知所先后。🍭
🍎☝☝☝☝☝我的CSDN☝☝☝☝☝☝🍓