力扣：通过《84.柱状图中最大的矩形》求解《85. 最大矩形》

news2024/11/22 11:15:17

84. 柱状图中最大的矩形
85. 最大矩形
84.柱状图中最大的矩形：
单调栈求解问题范围： 输出每个数左边第一个比它小的数
单调栈例题： Acwing 830. 单调栈

#include <iostream>

using namespace std;

const int N = 100010;
int stk[N],tt = 0;

int main()
{
    int n;
    cin>>n;
    for(int i = 0;i < n;i++)
    {
        int x;
        cin>>x;
        
        while(tt && stk[tt] >= x) tt--;
        if(!tt) cout<<"-1 ";
        else cout<<stk[tt]<<" ";
        stk[++tt] = x;
    }
    return 0;
}

思路：
寻找该最大矩形的左右边界，左边界是距离该矩形左边最近的最小的高度，有边界是距离该矩形右边最近的最小的高度，以图示例题为例：
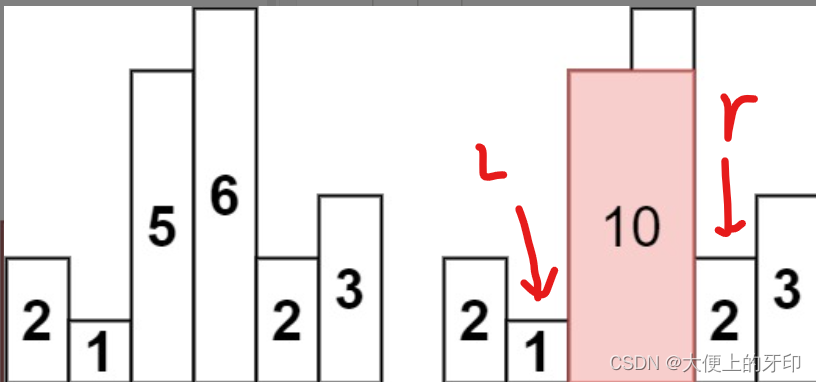
在这里插入图片描述
利用两次单调栈寻找左右边界，枚举每一个可存在的矩形，即可求解最大矩形。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n),right(n);
        stack<int> stk;
        //求左边界
        for(int i = 0;i < n;i++)
        {
            int x = heights[i];
            while(stk.size() && heights[stk.top()] >= x) stk.pop();
            if(stk.size()) left[i] = stk.top();
            else left[i] = -1;
            stk.push(i);
        }
        //求右边界
        stk = stack<int>();
        for(int i = n - 1;i >= 0;i--)
        {
            int x = heights[i];
            while(stk.size() && heights[stk.top()] >= x) stk.pop();
            if(stk.size()) right[i] = stk.top();
            else right[i] = n;
            stk.push(i);
        }
        int res = 0;
        for(int i = 0;i < n;i++)
        {
            res = max(res,heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
};

85. 最大矩形：
思路：
枚举每一行，对每一行求最大矩形面积。
预处理每行中每个位置对应的高度：
h[i][j]： 为第 i 行第 j 个数对应的高度
当 matrix[i][j] 为 "1” 时： $\rm h[i][j] = h[i - 1][j] + 1$

class Solution {
public:
    //84. 柱状图中最大的矩形代码
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n),right(n);
        stack<int> stk;

        for(int i = 0;i < n;i++)//求左边界
        {
            int x = heights[i];
            while(stk.size() && heights[stk.top()] >= x) stk.pop();
            if(stk.size()) left[i] = stk.top();
            else left[i] = -1;
            stk.push(i);
        }

        stk = stack<int>();
        for(int i = n - 1;i >= 0;i--)//求右边界
        {
            int x = heights[i];
            while(stk.size() && heights[stk.top()] >= x) stk.pop();
            if(stk.size()) right[i] = stk.top();
            else right[i] = n;
            stk.push(i);
        }
        int res = 0;
        for(int i = 0;i < n;i++)
        {
            res = max(res,heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
    int maximalRectangle(vector<vector<char>>& matrix) {
        if(matrix.empty() || matrix[0].empty()) return 0;
        int n = matrix.size(),m = matrix[0].size();
        vector<vector<int>> h(n,vector<int>(m));
        //预处理h[i][j]
        for(int i = 0;i < n;i++)
        {
            for(int j = 0;j < m;j++)
            {
                if(matrix[i][j] == '1')
                {
                    if(i) h[i][j] = h[i - 1][j] + 1;
                    else h[i][j] = 1;
                }
            }
        }
        //比较每一行中的最大矩形
        int res = 0;
        for(int i = 0;i < n;i++)
        {
            res = max(res,largestRectangleArea(h[i]));
        }
        return res;
    }
};