数据结构与算法基础-学习-21-查找之平衡二叉树（AVL树）

news2025/1/12 4:10:19

目录

 

一、个人理解

二、最小失衡子树

三、平衡调整的四种类型

1、LL型

2、RR型

3、LR型 

 4、RL型

四、如何平衡调整

1、LL型调整

2、LR型调整

五、宏定义

六、结构体类型定义

1、AVL树结点类型

2、AVL树类型

3、AVL树结点搜索路径类型

七、函数定义

1、初始化AVL树

2、新建一个AVL树结点

3、比较数据大小

4、数学中的LOG

5、初始化AVL树搜索路径

6、插入AVL树搜索路径

7、销毁AVL树搜索路径

8、RL型转换

9、LR型转换

10、RL型转换

11、LL型转换

12、RR型转换

13、AVL树转换

14、求AVL树的深度

15、计算结点平衡因子

16、插入数据到AVL树

17、销毁AVL树结点

 18、销毁AVL树

八、Linux环境测试LL型

 

一、个人理解

 

平衡二叉树（Balance Binary Tree）别名AVL树，是由三位科学家姓名首字母组成的。

它是二叉排序树（Binary Sort Tree简称BST）的一个衍生，具有BST所有的性质，除此之外还具有如下特性：

1、左子树和右子树的高度之差的绝对值小于等于1。

2、左子树和右子树也都是平衡二叉树。

 

为了方便区分这颗树是不是AVL树，加了一个参数平衡因子。

平衡因子 = 左子树高度 - 右子树高度

平衡因子为1，-1，0时，表示以这个节点为根的AVL树是平衡的。

 

二叉排序树（Binary Sort Tree简称BST）的介绍可以参考之前写的文章《数据结构与算法基础-学习-15-二叉树之前序、后序、中序遍历的递归和非递归方法实现以及BST的初始化、插入、获取结点数》

 

二、最小失衡子树

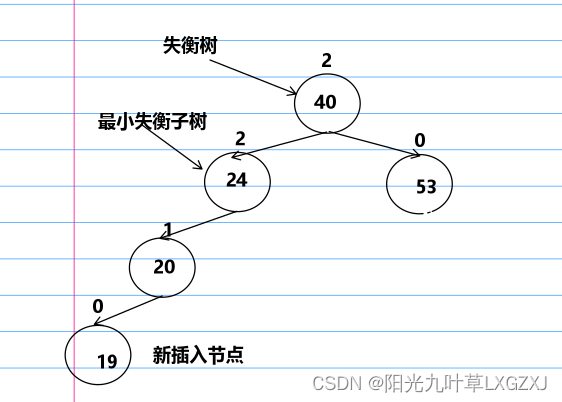
d2441dff98b040feb807c4d5cc07497e.png

 当插入新节点时，可能会出现多个失衡节点，这时我们需要找到最小失衡子树，如上图，再进行调整，变回AVL树。

 

三、平衡调整的四种类型

 

a：失衡节点。

b：a的孩子节点，c的双亲结点。

c：插入新节点的子树。

 

1、LL型

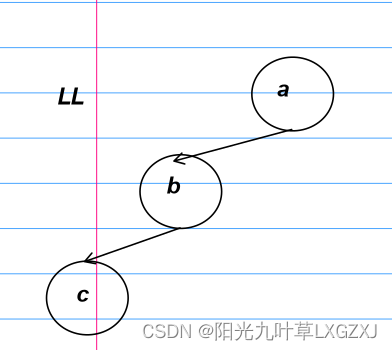
299201529e3d4287a9665232542a66be.png

2、RR型

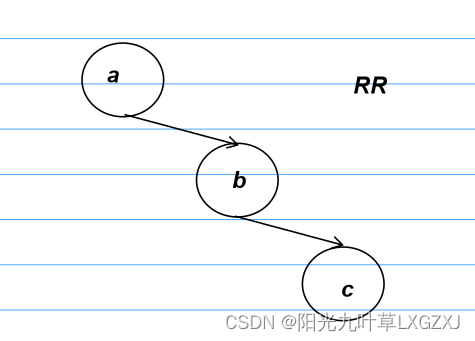
 17c6ef533e6743a0b4213ca713bb02cc.png

3、LR型 

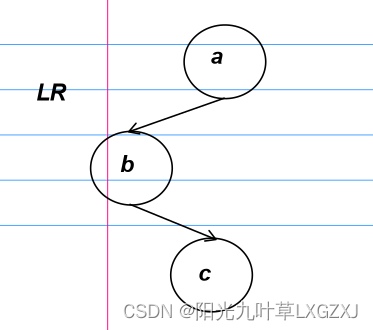
4a777bd27471421e80f34984891ab301.png

 4、RL型

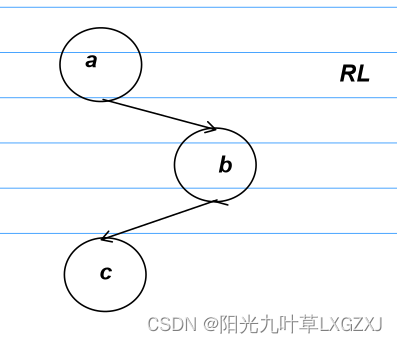
d3639ba3faa14f4c94eb880c9be61f0f.png

 

四、如何平衡调整

 

本文讲解其中两种LL，LR如何进行调整。

 

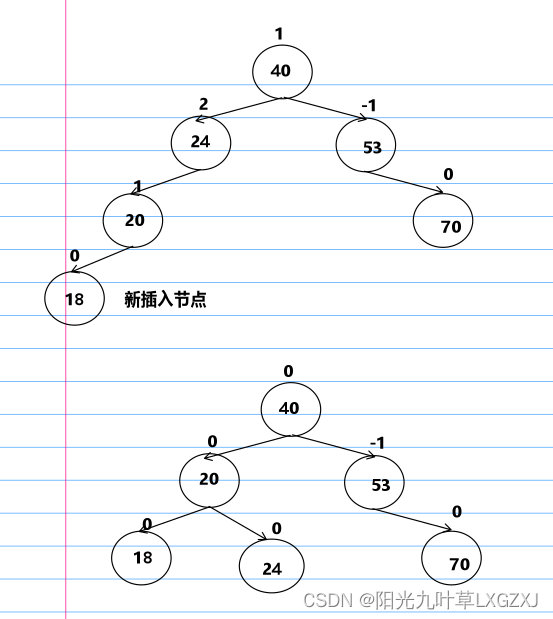
1、LL型调整

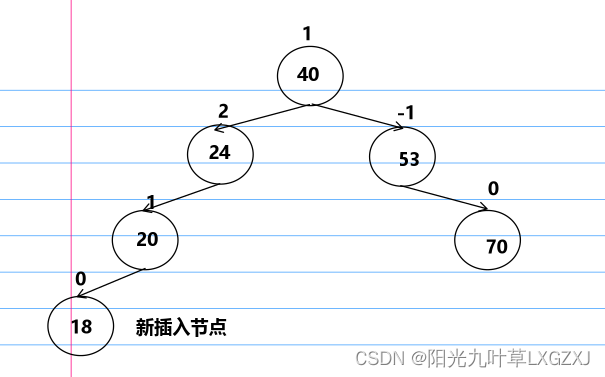
b530a45396ed46b88a374459f5a2b85e.png

 插入18，发现24结点出现失衡且为最小失衡子树，判断为LL型。

之后我们找到中间值结点，这里为20，我们把24挂到20的右侧上，这时需要注意20是否有右子树，如果有的话，需要挂到24的左子树上，最后断开24和40的链接，将20与40链接，如下图，重新计算平衡因子，已调整回平衡二叉树。

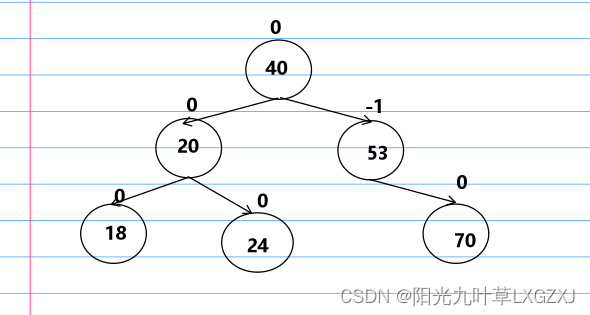
ed0a336e59cc4316952ad03187e363b2.png

 

2、LR型调整

 

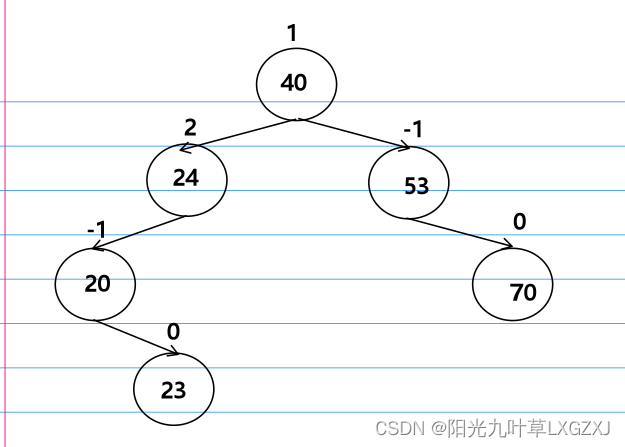
4771a149a3294c4d9cef470af20ef7f2.png

 

插入23，发现24结点出现失衡且为最小失衡子树，判断为LR型。

之后我们找到中间值结点，这里为23，断开24与40的链接，23和40进行链接，23如果有左孩子需要放到20的右指针上。如果23右右孩子的话，需要放到24的左指针上。23的左指针链接20，右指针链接24，如下图，重新计算平衡因子，已调整回平衡二叉树。

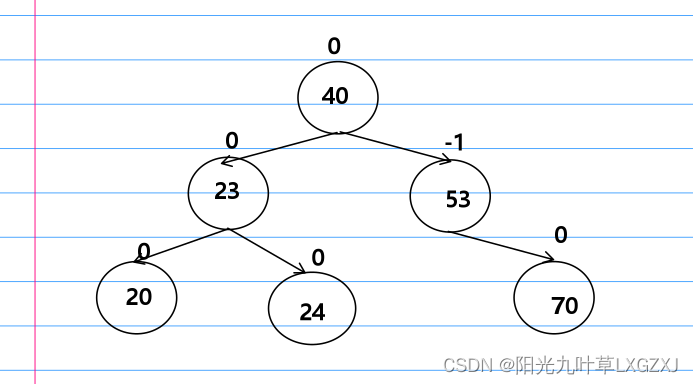
3961923aa4fa4211b9f7061861a2f8a7.png

五、宏定义

#define CMP_LARGE           0
#define CMP_LITTLE          1
#define CMP_EQUAL           2
#define BALANCE_FACTOR_INIT 0
#define AVL_BALANCE_FLAG    1
#define AVL_NO_BALANCE_FLAG 2
#define AVL_LEFT_DIRECTION  'l'
#define AVL_RIGHT_DIRECTION 'r'

六、结构体类型定义

1、AVL树结点类型

typedef struct AvlTreeNode
{
    AvlTreeNodeDataType Data;
    BalanceFactorType   BalanceFactor;
    struct AvlTreeNode* LeftNodePtr;
    struct AvlTreeNode* RightNodePtr;
}AvlTreeNode;
名称解释
Data存放数据。
BalanceFactor存放平衡因子。
LeftNodePtr存放左子树指针。
RightNodePtr存放右子树指针。

 

2、AVL树类型

typedef struct AvlTree
{
    AvlTreeNode*        RootNodePtr;
    AvlTreeNodeDataType TreeNodeNum;
}AvlTree;
名称解释
RootNodePtr存放AVL树根结点指针。
TreeNodeNum存放AVL树总结点数。

 

3、AVL树结点搜索路径类型

typedef struct AvlNodeSelectPathType
{
    AvlTreeNode**       NodePtrArray;
    AvlDirectionFlag*   DirectionArray;
    AvlTreeNodeDataType ArrayLen;
    AvlTreeNodeDataType ArrayMaxLen;
}AvlNodeSelectPathType;
名称解释
NodePtrArray存放AVL树插入数据时访问的结点指针。
DirectionArray存放AVL树插入数据时访问的方向标识（是左子树还是右子树）。
ArrayLen存放上述两个数组的实际使用长度。
ArrayMaxLen存放上述两个数组的最大使用长度。

其实也就是用了串的思想。

 

七、函数定义

 

1、初始化AVL树

Status InitAvlTree(AvlTree** AT)
{
    JudgeAllNullPointer(AT);
    *AT = (AvlTree*)MyMalloc(sizeof(AvlTree));
    (*AT)->RootNodePtr = NULL;
    (*AT)->TreeNodeNum = 0;
    Log("Init Avl Tree OK\n",Debug);
    return SuccessFlag;
}

 

2、新建一个AVL树结点

AvlTreeNode* NewAvlTreeNode(AvlTreeNodeDataType InputData)
{
    AvlTreeNode* NewNodePtr   = (AvlTreeNode*)MyMalloc(sizeof(AvlTreeNode));
    NewNodePtr->Data          = InputData;
    NewNodePtr->BalanceFactor = BALANCE_FACTOR_INIT;
    NewNodePtr->LeftNodePtr   = NULL;
    NewNodePtr->RightNodePtr  = NULL;
    //Log("New Avl Tree Node OK\n",Debug);
    return NewNodePtr;
}

 

3、比较数据大小

NumCmpType CmpAvlTreeNodeData(AvlTreeNodeDataType Data1, AvlTreeNodeDataType Data2)
{
    if(Data1 > Data2)
    {
        return CMP_LARGE;
    }
    else if(Data1 < Data2)
    {
        return CMP_LITTLE;
    }
    else
    {
        return CMP_EQUAL;
    }
}

 

4、数学中的LOG

//实现数学中的log，Num1为底数，Num2为对数。
//实现比较粗糙。以后改进。
AvlTreeNodeDataType MathLog(AvlTreeNodeDataType Num1, AvlTreeNodeDataType Num2)
{
    AvlTreeNodeDataType Cnt    = 1;
    AvlTreeNodeDataType TmpVal = Num1;
    while(TmpVal < Num2)
    {
        TmpVal = TmpVal * Num1;
        Cnt++;
    }
    return Cnt;
}

 

5、初始化AVL树搜索路径

Status InitAvlNodeSelectPath(AvlTree* AT, AvlNodeSelectPathType** SelectPath)
{
    JudgeAllNullPointer(AT);
    JudgeAllNullPointer(SelectPath);

    *SelectPath                   = (AvlNodeSelectPathType*)MyMalloc(sizeof(AvlNodeSelectPathType));
    (*SelectPath)->ArrayMaxLen    = MathLog(2,AT->TreeNodeNum) + 2;//平衡二叉树的最大高度,log2(n)+1,多加一个一节点，再加一。
    (*SelectPath)->NodePtrArray   = (AvlTreeNode**)MyMalloc(sizeof(AvlTreeNode*) * (*SelectPath)->ArrayMaxLen);
    (*SelectPath)->DirectionArray = (AvlDirectionFlag*)MyMalloc(sizeof(AvlDirectionFlag) * (*SelectPath)->ArrayMaxLen);
    (*SelectPath)->ArrayLen       = 0;

    Log("Init Avl Node Select Path OK\n",Debug);
    return SuccessFlag;    
}

 

6、插入AVL树搜索路径

Status InsertAvlNodeSelectPath(AvlNodeSelectPathType* SelectPath, AvlTreeNode* AvlTreeNodePtr, AvlDirectionFlag DirectionFlag)
{
    JudgeAllNullPointer(SelectPath);
    JudgeAllNullPointer(AvlTreeNodePtr);

    if(SelectPath->ArrayLen == SelectPath->ArrayMaxLen)
    {
        Log("Insert Avl Node Select Path Fail, reason : array is full.\n",Warning);
        return FailFlag;
    }

    SelectPath->NodePtrArray[SelectPath->ArrayLen]   = AvlTreeNodePtr;
    SelectPath->DirectionArray[SelectPath->ArrayLen] = DirectionFlag;
    SelectPath->ArrayLen++;

    Log("Insert Avl Node Select Path OK\n",Debug);
    return SuccessFlag; 
}

 

7、销毁AVL树搜索路径

Status DestoryAvlNodeSelectPath(AvlNodeSelectPathType** SelectPath)
{
    JudgeAllNullPointer(SelectPath);
    JudgeAllNullPointer(*SelectPath);

    free((*SelectPath)->NodePtrArray);
    free((*SelectPath)->DirectionArray);
    (*SelectPath)->ArrayMaxLen    = 0;
    (*SelectPath)->NodePtrArray   = NULL;
    (*SelectPath)->DirectionArray = NULL;
    (*SelectPath)->ArrayLen       = 0;
    free(*SelectPath);
    *SelectPath                   = NULL;

    Log("Destory Avl Node Select Path OK\n",Debug);
    return SuccessFlag;
}

 

8、RL型转换

Status RevoleRL(AvlNodeSelectPathType* SelectPath, AvlTreeNodeDataType StartIndex, AvlTreeNodeDataType EndIndex, AvlTreeNode** NewNodePtr)
{
    *NewNodePtr = SelectPath->NodePtrArray[EndIndex];
    SelectPath->NodePtrArray[StartIndex]->RightNodePtr    = (*NewNodePtr)->LeftNodePtr;
    SelectPath->NodePtrArray[StartIndex + 1]->LeftNodePtr = (*NewNodePtr)->RightNodePtr;
    (*NewNodePtr)->LeftNodePtr                            = SelectPath->NodePtrArray[StartIndex];
    (*NewNodePtr)->RightNodePtr                           = SelectPath->NodePtrArray[StartIndex + 1];
    
    Log("Revole RL OK\n",Debug);
    return SuccessFlag;
}

 

9、LR型转换

Status RevoleLR(AvlNodeSelectPathType* SelectPath, AvlTreeNodeDataType StartIndex, AvlTreeNodeDataType EndIndex, AvlTreeNode** NewNodePtr)
{
    *NewNodePtr = SelectPath->NodePtrArray[EndIndex];
    SelectPath->NodePtrArray[StartIndex]->LeftNodePtr      = (*NewNodePtr)->RightNodePtr;
    SelectPath->NodePtrArray[StartIndex + 1]->RightNodePtr = (*NewNodePtr)->LeftNodePtr;
    (*NewNodePtr)->LeftNodePtr                             = SelectPath->NodePtrArray[StartIndex + 1]; 
    (*NewNodePtr)->RightNodePtr                            = SelectPath->NodePtrArray[StartIndex];

    Log("Revole LR OK\n",Debug);
    return SuccessFlag;
}

 

10、RL型转换

Status RevoleRL(AvlNodeSelectPathType* SelectPath, AvlTreeNodeDataType StartIndex, AvlTreeNodeDataType EndIndex, AvlTreeNode** NewNodePtr)
{
    *NewNodePtr = SelectPath->NodePtrArray[EndIndex];
    SelectPath->NodePtrArray[StartIndex]->RightNodePtr    = (*NewNodePtr)->LeftNodePtr;
    SelectPath->NodePtrArray[StartIndex + 1]->LeftNodePtr = (*NewNodePtr)->RightNodePtr;
    (*NewNodePtr)->LeftNodePtr                            = SelectPath->NodePtrArray[StartIndex];
    (*NewNodePtr)->RightNodePtr                           = SelectPath->NodePtrArray[StartIndex + 1];
    
    Log("Revole RL OK\n",Debug);
    return SuccessFlag;
}

 

11、LL型转换

Status RevoleLL(AvlNodeSelectPathType* SelectPath, AvlTreeNodeDataType StartIndex, AvlTreeNodeDataType EndIndex, AvlTreeNode** NewNodePtr)
{
    *NewNodePtr = SelectPath->NodePtrArray[StartIndex + 1];
    SelectPath->NodePtrArray[StartIndex]->LeftNodePtr    = (*NewNodePtr)->RightNodePtr;
    (*NewNodePtr)->RightNodePtr                          = SelectPath->NodePtrArray[StartIndex];

    Log("Revole LL OK\n",Debug);
    return SuccessFlag;
}

 

12、RR型转换

Status RevoleRR(AvlNodeSelectPathType* SelectPath, AvlTreeNodeDataType StartIndex, AvlTreeNodeDataType EndIndex, AvlTreeNode** NewNodePtr)
{
    *NewNodePtr = SelectPath->NodePtrArray[StartIndex + 1];
    SelectPath->NodePtrArray[StartIndex]->RightNodePtr    = (*NewNodePtr)->LeftNodePtr;
    (*NewNodePtr)->LeftNodePtr                            = SelectPath->NodePtrArray[StartIndex]; 

    Log("Revole RR OK\n",Debug);
    return SuccessFlag;
}

 

13、AVL树转换

Status RevoleAvlTree(AvlNodeSelectPathType* SelectPath, AvlTreeNodeDataType StartIndex, AvlTreeNodeDataType EndIndex, AvlTreeNode** NewNodePtr)
{
    JudgeAllNullPointer(SelectPath);
    JudgeAllNullPointer(NewNodePtr);

    if(SelectPath->DirectionArray[StartIndex] == AVL_LEFT_DIRECTION)
    {
        if(SelectPath->DirectionArray[StartIndex + 1] == AVL_LEFT_DIRECTION)//LL
        {
            RevoleLL(SelectPath, StartIndex, EndIndex, NewNodePtr);
        }
        else//LR
        {
            RevoleLR(SelectPath, StartIndex, EndIndex, NewNodePtr);
        }
    }
    else
    {
        if(SelectPath->DirectionArray[StartIndex + 1] == AVL_LEFT_DIRECTION)//RL
        {
            RevoleRL(SelectPath, StartIndex, EndIndex, NewNodePtr);
        }
        else//RR
        {
            RevoleRR(SelectPath, StartIndex, EndIndex, NewNodePtr);
        }
    }
    return SuccessFlag;
}

就是把RR,RL,LL,LR进行封装了一层。

 

14、求AVL树的深度

AvlTreeNodeDataType GetAvlTreeDepth(AvlTreeNode* NodePtr)
{
    if(NodePtr == NULL)
    {
        return 0;
    }
    else
    {
        AvlTreeNodeDataType l = GetAvlTreeDepth(NodePtr->LeftNodePtr);
        AvlTreeNodeDataType r = GetAvlTreeDepth(NodePtr->RightNodePtr);
        if(l >= r)
        {
            return l + 1;
        }
        else
        {
            return r + 1;
        }
    }
}

详细的实现和思路可以参考之前写的文章《数据结构与算法基础-学习-16-二叉树之层次遍历、创建树、复制树、销毁树，获取树的深度、结点数、叶子结点数》

 

15、计算结点平衡因子

Status ComputeAvlNodeBalanceFactor(AvlTreeNode* NodePtr)
{
    JudgeAllNullPointer(NodePtr);
    NodePtr->BalanceFactor = GetAvlTreeDepth(NodePtr->LeftNodePtr) - GetAvlTreeDepth(NodePtr->RightNodePtr);
    Log("Compute Avl Node Balance Factor OK\n",Debug);
    return SuccessFlag;
}

给出需要重新计算平衡因子的Avl树的节点，即可把此节点的平衡因子重新计算一次。
 

16、插入数据到AVL树

//假设Avl树中没有相同元素，根节点大于左子树，小于右子树。
Status AddAvlTreeNode(AvlTree* AT, AvlTreeNodeDataType InputData)
{
    JudgeAllNullPointer(AT);
    if(AT->RootNodePtr == NULL)
    {
        AT->RootNodePtr = NewAvlTreeNode(InputData);
        AT->TreeNodeNum++;
        Log("Add Avl Tree Root Node OK\n",Debug);
        return SuccessFlag;
    }

    AvlTreeNode* TmpPtr               = AT->RootNodePtr;
    AvlNodeSelectPathType* SelectPath = NULL;
    InitAvlNodeSelectPath(AT, &SelectPath);

    while(TmpPtr)
    {
        if(CmpAvlTreeNodeData(TmpPtr->Data, InputData) == CMP_LARGE)
        {
            InsertAvlNodeSelectPath(SelectPath, TmpPtr, AVL_LEFT_DIRECTION);
            if(TmpPtr->LeftNodePtr == NULL)
            {
                TmpPtr->LeftNodePtr = NewAvlTreeNode(InputData);
                AT->TreeNodeNum++;
                InsertAvlNodeSelectPath(SelectPath, TmpPtr->LeftNodePtr, AVL_LEFT_DIRECTION);
                break;
            }
            TmpPtr = TmpPtr->LeftNodePtr;
        }
        else if(CmpAvlTreeNodeData(TmpPtr->Data, InputData) == CMP_LITTLE)
        {
            InsertAvlNodeSelectPath(SelectPath, TmpPtr, AVL_RIGHT_DIRECTION);
            if(TmpPtr->RightNodePtr == NULL)
            {
                TmpPtr->RightNodePtr = NewAvlTreeNode(InputData);
                AT->TreeNodeNum++;
                InsertAvlNodeSelectPath(SelectPath, TmpPtr->RightNodePtr, AVL_RIGHT_DIRECTION);
                break;
            }
            TmpPtr = TmpPtr->RightNodePtr;
        }
        else
        {
            Log("AddAvlTreeNode function not supported : same element.\n",Debug);
            Log("Add Avl Tree Node Fail\n",Debug);
            return FailFlag;
        }
    }
    PrintfAvlNodeSelectPath(SelectPath);

    //Avl树搜索路径收集完成。
    //倒叙遍历搜索路径，也就是从叶子节点遍历到根节点。
    //如果叶子节点的父节点的平衡因子从1或-1变为0，搜索路径上的其他节点平衡因子不变。
    if(SelectPath->DirectionArray[SelectPath->ArrayLen - 2] == AVL_LEFT_DIRECTION)
    {
        (SelectPath->NodePtrArray[SelectPath->ArrayLen - 2]->BalanceFactor)++;
    }
    else
    {
        (SelectPath->NodePtrArray[SelectPath->ArrayLen - 2]->BalanceFactor)--;
    }

    if(SelectPath->NodePtrArray[SelectPath->ArrayLen - 2]->BalanceFactor == 0)//平衡二叉树的平衡因子不会发生变化的情况
    {
        DestoryAvlNodeSelectPath(&SelectPath);
        Log("Add Avl Tree Node OK, Balance Factor No Change.\n",Debug);
        return SuccessFlag;
    }

    //平衡二叉树的平衡因子会发生变化的情况,需要按照情况讨论。
    //从倒数第二个节点开始计算平衡因子。
    AvlTreeNodeDataType i;
    for(i = SelectPath->ArrayLen - 3; i >= 0; i--)
    {
        if(SelectPath->DirectionArray[i] == AVL_LEFT_DIRECTION)
        {
            (SelectPath->NodePtrArray[i]->BalanceFactor)++;
        }
        else
        {
            (SelectPath->NodePtrArray[i]->BalanceFactor)--;
        }

        if(JudgeBalanceFactorStatus(SelectPath->NodePtrArray[i]->BalanceFactor) == AVL_NO_BALANCE_FLAG)
        {
            Log("Find Avl Tree Node No Balance.\n",Debug);
            break;
        }
    }

    if(i != -1)//表示搜索路径没有遍历完，某节点出现了不平衡因子
    {
        //进行LL,LR,RR,RL
        AvlTreeNode* NewNodePtr = NULL;
        RevoleAvlTree(SelectPath, i, i + 2, &NewNodePtr);

        if(i != 0)//除根节点以外的节点出现节点有不平衡因子，在LL,LR,RR,RL之后，需要把转换之后的子树连回Avl树。
        {
            if(SelectPath->DirectionArray[i - 1] == AVL_LEFT_DIRECTION)
            {
                SelectPath->NodePtrArray[i - 1]->LeftNodePtr = NewNodePtr;
            }
            else
            {
                SelectPath->NodePtrArray[i - 1]->RightNodePtr = NewNodePtr;
            }
        }
        else//根节点出现不平衡因子，在LL,LR,RR,RL之后，需要把转换之后的Avl树根节点放回RootNodePtr。
        {
            AT->RootNodePtr = NewNodePtr;
        }
        //重算平衡因子,只算最小平衡树根节点开始的三个节点的平衡因子即可。 
        AvlTreeNodeDataType j;
        for(j = i; j <= i + 2; j++)
        {
            ComputeAvlNodeBalanceFactor(SelectPath->NodePtrArray[j]);
        }
    }
    
    DestoryAvlNodeSelectPath(&SelectPath);
    Log("Add Avl Tree Node OK.\n",Debug);
    return SuccessFlag; 
}

（1）、插入的数据比根节点小，插入到左子树中，不然插入到右子树中，且把走过的结点指针压入搜索路径SelectPath中，此实现暂时只支持不相同值的插入。

 

（2）、插入完后，通过SelectPath检查插入结点的双亲结点，看其平衡因子是不是变化为0，如果是，说明双亲结点是平衡结点且左右孩子指针都有数据结点。不用需要进行平衡转换，结束。

 

（3）、如果不是0，倒序遍历SelectPath，计算平衡因子，如果出现没有不平衡结点，结束。

 

（4）、如果出现不平衡结点，进行平衡转换RevoleAvlTree，转换之后判断是不是根结点，不是重新链回原AVL树，如果是更新RootNodePtr结点。

 

（5）、重新计算不平衡结点开始的三个结点的平衡因子，就可以了，因为三个节点之后的结点在步骤3已经计算出来了，转换不会影响平衡因子的变化。

 

（6）、三个结点之前的结点不用重新计算，因为平衡了，所以不影响（这一步我测试了几组数据，都正确）。

 

17、销毁AVL树结点

Status DestoryAvlTreeNode(AvlTreeNode** RootPTR)
{
    if(*RootPTR == NULL)
    {
        return SuccessFlag;
    }
    else
    {
        DestoryAvlTreeNode(&((*RootPTR)->LeftNodePtr));
        DestoryAvlTreeNode(&((*RootPTR)->RightNodePtr));
        free(*RootPTR);
        *RootPTR = NULL;
        Log("Destroy Avl Tree Node OK\n",Debug);
    }
    return SuccessFlag;
}

 

 18、销毁AVL树

Status DestoryAvlTree(AvlTree** AvlTree)
{
    DestoryAvlTreeNode(&((*AvlTree)->RootNodePtr));
    (*AvlTree)->RootNodePtr = NULL;
    (*AvlTree)->TreeNodeNum = 0;
    free(*AvlTree);
    *AvlTree                = NULL;
    Log("Destroy Avl Tree OK\n",Debug);
    return SuccessFlag;
}

 

八、Linux环境测试LL型

747ad538c34b4534bc6faa98b7f306e3.png

 

[root@czg2 Select]# make
gcc -Wall -O3 ../Log/Log.c ../PublicFunction/PublicFunction.c Select.c HashTable.c AvlTree.c main.c -o TestSelect -I ../Log/ -I ../PublicFunction/ -I ./ -I ../PublicFunction/SqStack/

[root@czg2 Select]# ./TestSelect 
[2023-4]--[ Debug ]--Init Avl Tree OK
[2023-4]--[ Debug ]--Add Avl Tree Root Node OK
[2023-4]--[ Debug ]--Init Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Printf Avl Node Select Path
[(0x1738fe0,l),(0x1739320,l)]
ArrayLen : 2, ArrayMaxLen : 3
[2023-4]--[ Debug ]--Destory Avl Node Select Path OK
[2023-4]--[ Debug ]--Add Avl Tree Node OK.
[2023-4]--[ Debug ]--Init Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Printf Avl Node Select Path
[(0x1738fe0,r),(0x1739350,r)]
ArrayLen : 2, ArrayMaxLen : 3
[2023-4]--[ Debug ]--Destory Avl Node Select Path OK
[2023-4]--[ Debug ]--Add Avl Tree Node OK, Balance Factor No Change.
[2023-4]--[ Debug ]--Init Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Printf Avl Node Select Path
[(0x1738fe0,l),(0x1739320,l),(0x17393b0,l)]
ArrayLen : 3, ArrayMaxLen : 4
[2023-4]--[ Debug ]--Destory Avl Node Select Path OK
[2023-4]--[ Debug ]--Add Avl Tree Node OK.
[2023-4]--[ Debug ]--Init Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Printf Avl Node Select Path
[(0x1738fe0,r),(0x1739350,r),(0x17393e0,r)]
ArrayLen : 3, ArrayMaxLen : 4
[2023-4]--[ Debug ]--Destory Avl Node Select Path OK
[2023-4]--[ Debug ]--Add Avl Tree Node OK.
[2023-4]--[ Debug ]--Init Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Insert Avl Node Select Path OK
[2023-4]--[ Debug ]--Printf Avl Node Select Path
[(0x1738fe0,l),(0x1739320,l),(0x17393b0,l),(0x1739410,l)]
ArrayLen : 4, ArrayMaxLen : 5
[2023-4]--[ Debug ]--Find Avl Tree Node No Balance.
[2023-4]--[ Debug ]--Revole LL OK
[2023-4]--[ Debug ]--Compute Avl Node Balance Factor OK
[2023-4]--[ Debug ]--Compute Avl Node Balance Factor OK
[2023-4]--[ Debug ]--Compute Avl Node Balance Factor OK
[2023-4]--[ Debug ]--Destory Avl Node Select Path OK
[2023-4]--[ Debug ]--Add Avl Tree Node OK.
Ptr : 0x1739410, Data : 18    , BalanceFactor : 0 , LeftNodePtr : (nil)     , RightNodePtr : (nil)
Ptr : 0x17393b0, Data : 20    , BalanceFactor : 0 , LeftNodePtr : 0x1739410 , RightNodePtr : 0x1739320
Ptr : 0x1739320, Data : 24    , BalanceFactor : 0 , LeftNodePtr : (nil)     , RightNodePtr : (nil)
Ptr : 0x1738fe0, Data : 40    , BalanceFactor : 0 , LeftNodePtr : 0x17393b0 , RightNodePtr : 0x1739350
Ptr : 0x1739350, Data : 53    , BalanceFactor : -1, LeftNodePtr : (nil)     , RightNodePtr : 0x17393e0
Ptr : 0x17393e0, Data : 70    , BalanceFactor : 0 , LeftNodePtr : (nil)     , RightNodePtr : (nil)
[2023-4]--[ Debug ]--Destroy Avl Tree Node OK
[2023-4]--[ Debug ]--Destroy Avl Tree Node OK
[2023-4]--[ Debug ]--Destroy Avl Tree Node OK
[2023-4]--[ Debug ]--Destroy Avl Tree Node OK
[2023-4]--[ Debug ]--Destroy Avl Tree Node OK
[2023-4]--[ Debug ]--Destroy Avl Tree Node OK
[2023-4]--[ Debug ]--Destroy Avl Tree OK

 

 

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/457416.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于CMS项目的JDBC的实战

基于CMS项目的JDBC的实战

基于CMS项目的JDBC的实战 使用的Javase技术&#xff0c;进行控制台输出的客户管理系统&#xff08;CMS&#xff09;&#xff0c;主要功能包含登录&#xff0c;注册、客户信息的展示&#xff0c;客户信息的更新&#xff0c;客户信息添加删除客户、退出系统。 设计创建数据库 …
阅读更多...
PEX高效批量网络装机

PEX高效批量网络装机

目录 一、部署PXE远程安装服务 1&#xff09;PXE概述 若要搭建PEX网络体系&#xff0c;必须满足以下几个前提条件 2&#xff09;搭建PXE远程安装服务器 ①安装并启用 TFTP 服务 ②安装并启用 DHCP 服务 ​编辑 ③准备 Linux 内核、初始化镜像文件 ④准备 PXE 引导程序 …
阅读更多...
CUDA下载与对应版本查询

CUDA下载与对应版本查询

文章目录 1 算力&#xff0c;CUDA Driver Version&#xff0c;CUDA Runtime Version2 显卡型号3 实操4 镜像 1 算力&#xff0c;CUDA Driver Version&#xff0c;CUDA Runtime Version 比如说我们进入pytorch官网中&#xff0c;点击下载&#xff0c;如何找到适合自己的CUDA版本…
阅读更多...
SCAU 统计学 实验5

SCAU 统计学 实验5

8.14 总体平均值&#xff08;μ&#xff09;&#xff1a;7.0 cm 总体方差&#xff08;σ&#xff09;&#xff1a;0.03 cm 样本平均值&#xff08;x̄&#xff09;&#xff1a;6.97 cm 样本方差&#xff08;s&#xff09;&#xff1a;0.0375 cm 样本大小&#xff08;n&#xff…
阅读更多...
复旦MOSS大模型开源了！Github和Hugging Face同时上线

复旦MOSS大模型开源了！Github和Hugging Face同时上线

来源&#xff1a;量子位 复旦大模型MOSS&#xff0c;正式开源了&#xff01; 作为国内首个开放测试的类ChatGPT产品&#xff0c;MOSS开源地址一放出&#xff0c;又冲上知乎热搜&#xff1a; 从官网介绍来看&#xff0c;MOSS是一个拥有160亿参数的开源对话语言模型。 它由约7…
阅读更多...
EventLog Analyzer：高效保护网络安全的强大工具

EventLog Analyzer：高效保护网络安全的强大工具

网络安全是当今数字化世界中最为重要的话题之一。随着越来越多的组织、企业和个人将其业务转移到互联网上&#xff0c;网络安全问题变得越来越严峻。针对这个问题&#xff0c;EventLog Analyzer提供了一个有效的解决方案&#xff0c;让网络管理员可以更好地监控和保护其网络环境…
阅读更多...
【虚拟仿真】Unity3D中实现UI的单击、双击、按压、拖动的不同状态判断

【虚拟仿真】Unity3D中实现UI的单击、双击、按压、拖动的不同状态判断

推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好&#xff0c;我是佛系工程师☆恬静的小魔龙☆&#xff0c;不定时更新Unity开发技巧&#xff0c;觉得有用记得一键三连哦。 一、前言 之前写了一篇在Unity中鼠标的单击、双击、拖动的文章&#xff…
阅读更多...
Improving Language Understanding by Generative Pre-Training 论文阅读

Improving Language Understanding by Generative Pre-Training 论文阅读

论文题目&#xff1a;通过生成式预训练提高语言理解能力 GPT的全称&#xff1a;Generative Pre-trained Transformer。 Generative是指GPT可以利用先前的输入文本来生成新的文本。GPT的生成过程是基于统计的&#xff0c;它可以预测输入序列的下一个单词或字符&#xff0c;从而生…
阅读更多...
春招，进阿里了....

春招，进阿里了....

个人背景是东北某 985 科班本硕&#xff0c;做的 测试开发&#xff0c;有两个自己写的小项目。下面是一些印象比较深刻的面试题 阿里一面 什么是软件测试&#xff1f; 软件测试过程中会面向哪些群体&#xff1f; 开发一个软件都要经过哪些阶段&#xff1f; 什么是黑盒测试&…
阅读更多...
一块钱看Android Debug： avc denied 已存在的目录不能访问

一块钱看Android Debug： avc denied 已存在的目录不能访问

某三方应用&#xff0c;使用了USB摄像头&#xff0c;启动应用后功能不能使用&#xff0c;看log有如下错误&#xff0c; denied后面{}里的是要执行的动作,比如append,open,execmod,link等等 scontext指的是域,对应的是te文件 上面报错这条对应te文件是untrusted_app.te, scontex…
阅读更多...
如何将 WhatsApp 聊天添加到您的网站

如何将 WhatsApp 聊天添加到您的网站

WhatsApp是全球最受欢迎的消息传递应用程序。平台上有超过 2 亿活跃用户与朋友、家人和企业进行交流。对于企业而言&#xff0c;WhatsApp 是与客户进行个人、可访问和非正式对话的理想渠道。 要将 WhatsApp 作为渠道引入您的客户旅程&#xff0c;第一步是将 WhatsApp 聊天按钮…
阅读更多...
2023软件测试工具大全（自动化、接口、性能、安全、测试管理）

2023软件测试工具大全（自动化、接口、性能、安全、测试管理）

目录 前言 一、自动化测试工具 Selenium Appium TestComplete 二、接口测试工具 Postman SoapUI JMeter 三、性能测试工具 LoadRunner JMeter Gatling 四、安全测试工具 Burp Suite OWASP ZAP Nmap 五、测试管理工具 TestRail JIRA TestLink 总结 前言 …
阅读更多...
【JavaScript】this理解总结

【JavaScript】this理解总结

概念 this是函数运行时所在的对象。 使用场合 1.全局环境 全局环境使用this&#xff0c;this指向顶层对象。 2.构造函数 构造函数体里面的this&#xff0c;this指向是构造出来的实例对象。 3.对象的方法 ● 如果对象的方法里面包含this&#xff0c;this的指向就是方法运…
阅读更多...
ASPICE详细介绍-4.车载项目为什么要符合ASPICE标准？

ASPICE详细介绍-4.车载项目为什么要符合ASPICE标准？

目录 车载项目为什么要符合ASPICE标准&#xff1f;ASPICE与功能安全的关系、区别&#xff1f;各大车厂对软件体系的要求 车载项目为什么要符合ASPICE标准&#xff1f; ASPICE&#xff08;Automotive Software Process Improvement and Capability Determination&#xff09;最…
阅读更多...
sacrebleu找不到报错（无法直接下载）

sacrebleu找不到报错（无法直接下载）

网络问题无法下载&#xff0c;下载下来py文件&#xff0c;放到同级目录下面 https://raw.githubusercontent.com/huggingface/datasets/2.11.0/metrics/sacrebleu/sacrebleu.py然后注释掉版本报错
阅读更多...
Devops和Gitops区别

Devops和Gitops区别

一. 什么是devops DevOps 是一种开发&#xff08;Dev&#xff09;和运维&#xff08;Ops&#xff09;之间协作和沟通的文化、流程和工具的实践方法。它强调迭代、快速交付和持续集成/持续交付&#xff0c;旨在加速软件交付的速度、质量和稳定性。 DevOps 的核心目标是通过自动…
阅读更多...
中国视频云市场报告：腾讯云连续五年解决方案市场份额第一

中国视频云市场报告：腾讯云连续五年解决方案市场份额第一

4月24日&#xff0c;全球领先的IT市场研究和咨询公司IDC发布《中国视频云市场跟踪&#xff08;2022下半年&#xff09;》报告&#xff0c;腾讯云音视频的解决方案市场份额已连续五年排名第一&#xff0c;斩获自2018年IDC对外发布数据以来的“五年连冠”。其中&#xff0c;腾讯云…
阅读更多...
C++模板使用

C++模板使用

感谢你的阅读&#xff01;&#xff01;&#xff01; 目录 感谢你的阅读&#xff01;&#xff01;&#xff01; 举个例子&#xff1a; template 有什么意义为什么要用模板 与typedef的区别 使用方法 模板&#xff1a;隐式实例化与显示实例化 和非模板函数以及多个模板类…
阅读更多...
SAP ABAP MARA-MSBOOKPARTNO 制造商登记部分编号

SAP ABAP MARA-MSBOOKPARTNO 制造商登记部分编号

BAPI_MATERIAL_SAVEDATA CLIENTDATA结构无此字段。 DATA:LS_TE_MARA TYPE BAPI_TE_MARA. DATA:LS_TE_MARAX TYPE BAPI_TE_MARAX. DATA:LT_BAPIPAREX TYPE TABLE OF BAPIPAREX. DATA:LS_BAPIPAREX TYPE BAPIPAREX. …
阅读更多...
Spring Bean作用域与生命周期

Spring Bean作用域与生命周期

目录 Bean的作用域&#xff1a; Bean有六大行为模式 1、singleton:单例模式(默认) 2、prototype: 原型模式(多例模式) 3、request: 请求作用域(Spring MVC) 4、session: 会话作用域(Spring MVC) 5、application: 全局作用域(Spring MVC) 6、websocket: HTTP WebSocket …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023