框架

第一步：定义s[i][j]存储i到j的(最短)路径长度，并按如下顺序进行初始化：
- 自己到自己的长度初始化为0
- 其他两点赋予Integer.MAX_VALUE/2。（防止两个最大值相加时溢出）
- 最后赋值题目已知的某两点距离

// 节点从1-n
int[][] s = new int[n+1][n+1]; // s[i][j]表示i到j的（最小）距离
// 数据初始化（到自己是0）
for(int i = 1; i <= n; i++)
	for(int j = 1; j <= n; j++){
		if(i==j)
			s[i][j] = 0; // 自己到自己为0
		else s[i][j] = Integer.MAX_VALUE/2;// 没有通路，赋予最大值
	}

for(int i = 0;i < times.length;i++){
	s[起点][终点] = 题目已给出的两点间的距离（权重）;
}

第二步：弗洛伊德算法核心，三个For循环（递推式部分）
- 当经过k时的i到j的距离s[i][k]+s[k][j]比已知距离s[i][j]小，则更新s[i][j]。（此步骤在《算法导论》中称之为松弛Relaxation）

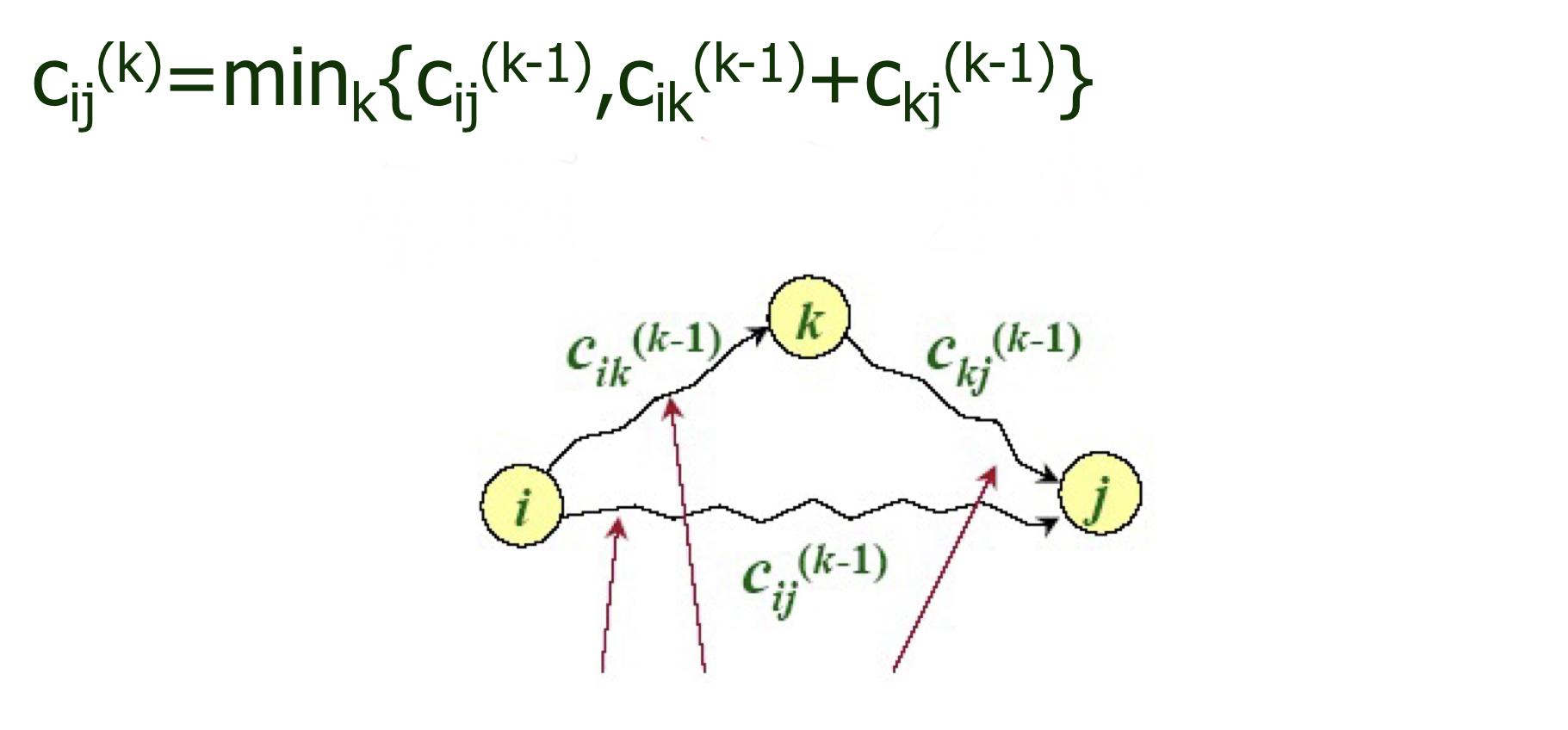
在这里插入图片描述

// 第二步：弗洛伊德算法
for(int k = 1;k <= n;k++){
   // 计算经过k节点时，i到j的最短路径长度
   for(int i = 1;i <= n;i++){
      for(int j = 1; j<= n;j++){
         s[i][j] = Math.min(s[i][j],s[i][k]+s[k][j]);
      }
   }
}

第三步：查看s[i][j]任意两点之间的最短路径只要不是Integer.MAX_VALUE/2，便可达。

时间复杂度为O(n^3)

实战

题目链接 LeetCode 中等 743. 网络延迟时间

按照如上模板进行解答：

class Solution {

    int[][] s;
    public int networkDelayTime(int[][] times, int n, int k) {
		s = new int[n+1][n+1]; // s[i][j]表示i到j的（最小）距离
		// 数据初始化（到自己是0）
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= n; j++){
				if(i==j)
					s[i][j] = 0; // 自己到自己为0
				else s[i][j] = Integer.MAX_VALUE/2;// 没有通路，赋予最大值
			}

		for(int i = 0;i < times.length;i++){
			s[times[i][0]][times[i][1]] = times[i][2];
		}
		// 弗洛伊德算法
		for(int m = 1;m <= n;m++){
			 // 计算经过m节点时，更新i到j的最短路径长度
			for(int i = 1;i <= n;i++){
				for(int j = 1; j<= n;j++){
					s[i][j] = Math.min(s[i][j],s[i][m]+s[m][j]);
				}
			}
		}
		// 寻找k到每个节点的最大距离
		int result  = 0;
		for(int i = 1;i <= n;i++){
			result = Math.max(result,s[k][i]);
		}
		if(result == Integer.MAX_VALUE/2){
			return -1;
		}
		return result;
    }
}