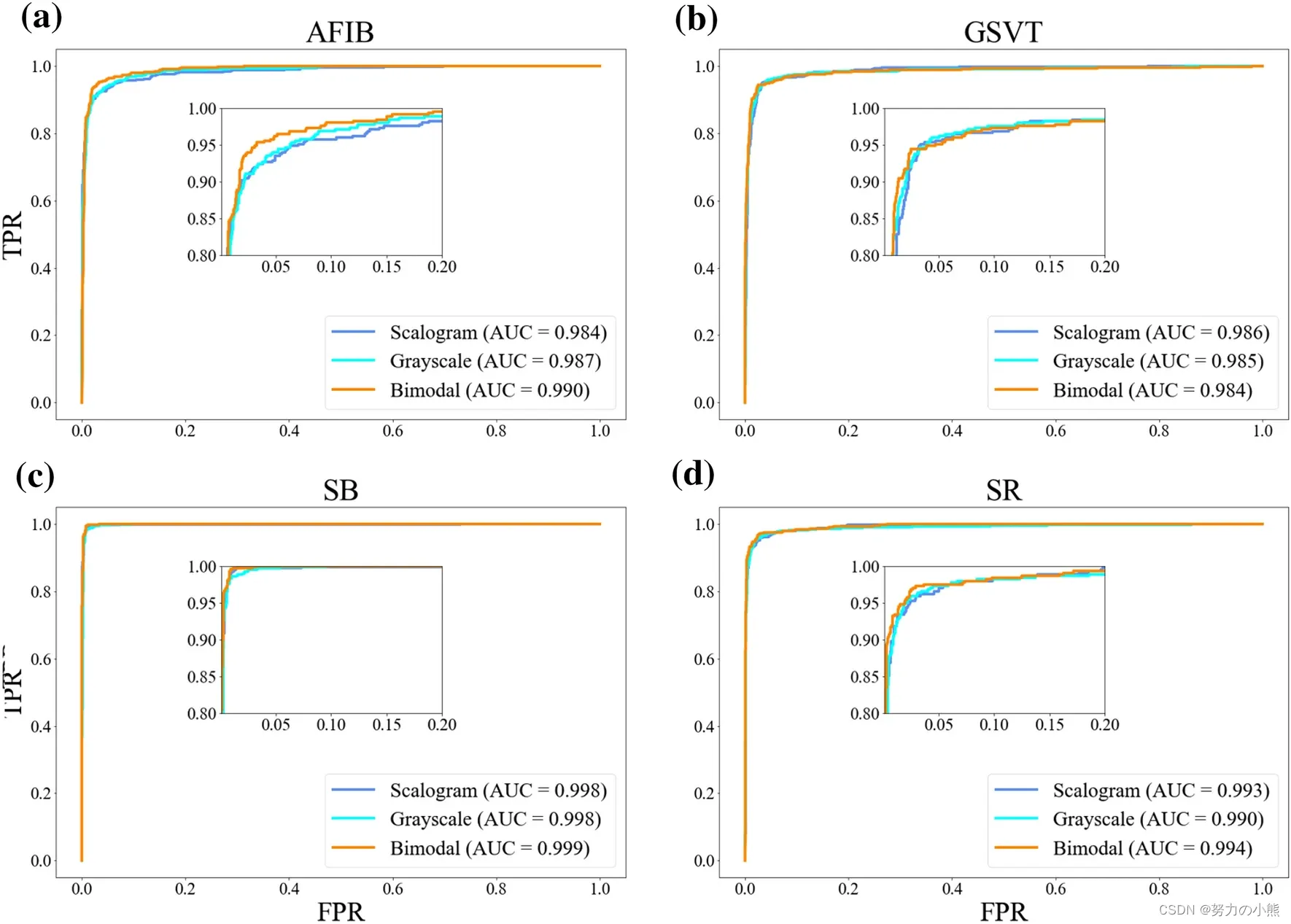
欧拉函数
欧拉函数表示的是1-n中与n互质数的个数。
如1-6中:1,5都和6互质,因此互质数为2
欧拉函数分解质因数后表示为:

互质数个数可表示为
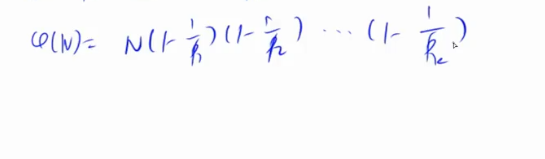

int main()
{
int n;
cin >> n;
while(n--)
{
int a;
cin >> a;
//分解质因数
int res = a;
for (int i = 2; i <= a / i; ++i)
{
if (a % i == 0)//如果a能整除i,说明i是质因子
{
//i是a的质因子
res = res / i * (i- 1);// res* (1 - 1 / a);这俩式子等价
while (a % i == 0)//把i除干净
{
a /= i;
}
}
}
if (a > 1)//a有一个大的质因子
res = res / a * (a-1);
cout << res << endl;
}
return 0;
}筛法求欧拉函数
如果求1-n的每个欧拉函数上面的方法就比较复杂,我们用筛法求欧拉函数比较简单。
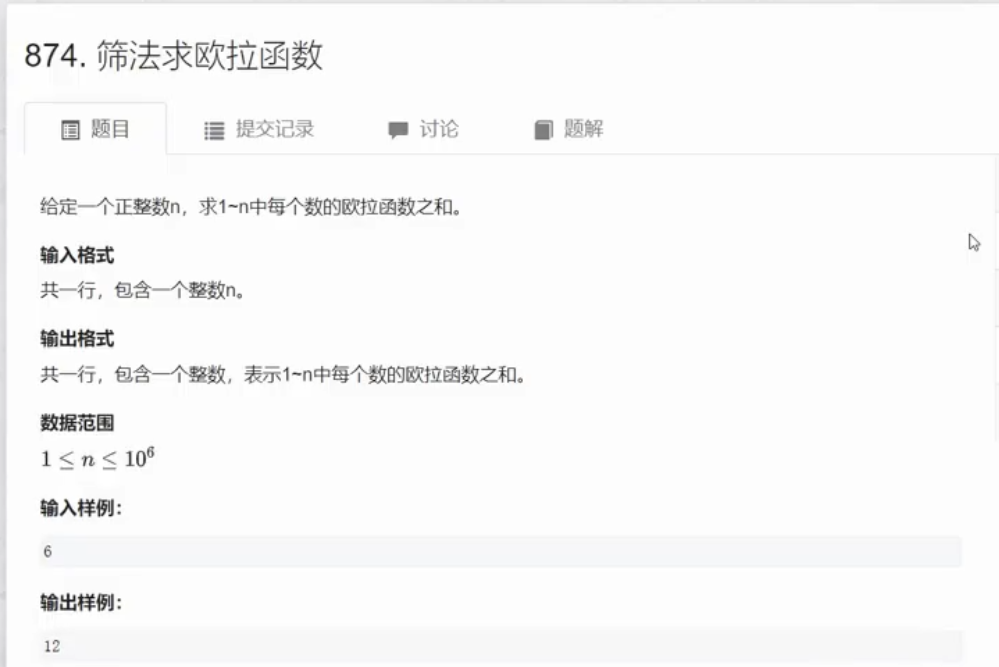
如果一个数为n,而且该数是质数,则从1到n-1所有的数都与它互质,即有n-1个数跟它互质。
给这个公式乘i,即α (pj,i)比α(i)多了一项pj ,即分解质因数后多乘了一个pj
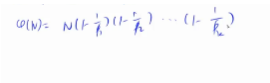
乘j之后欧拉函数是这样,即α (pj,i)=pj*α(i)


当i%pj不等于0时

const int N = 1000010;
int n;
int primes[N];//存每一个质数
int cnt;//质数的下标
bool st[N];//每个数是否被筛掉
int phi[N];//存储欧拉函数
typedef long long LL;
LL get_eulers(int n)
{
phi[1] = 1;
//线性筛法
for (int i = 2; i <= n ; ++i)
{
if (!st[i])//如果当前数没有被筛过,就说明当前是质数
{
primes[cnt++] = i;
phi[i] = i - 1;//有i-1个数跟它互质
}
for (int j = 0; primes[j] <= n / i; j++)//从小到大枚举所有的质数
{
st[primes[j] * i] = true;
if (i % primes[j] == 0)//如果当前数模primes[j]为0
{
phi[primes[j] * i] = phi[i]* primes[j];//α (pj,i)=pj*α(i)
break;
}
phi[primes[j] *i] = phi[i] * (primes[j] - 1);
}
}
LL res = 0;
for (int i = 1; i <=n ; ++i)
{
res += phi[i];
}
return res;
}
int main()
{
int n;
cin >> n;
cout<<get_eulers(n)<<endl;
return 0;
}三条横线是余数
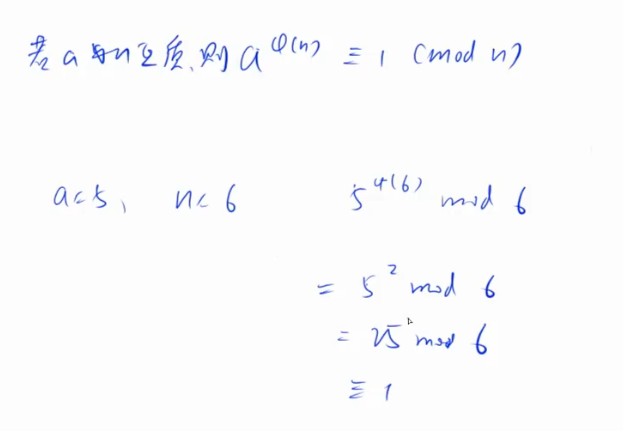
快速幂
快速的求出来a的k次方模p的结果。

快速幂预处理出这些值

目标就是把k拆成下面这种形式
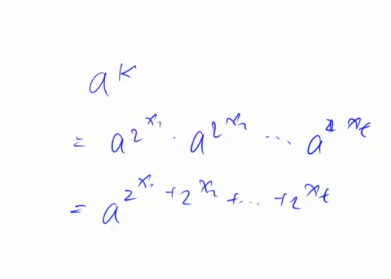
把K化成二进制,二进制表示里面所有是1的位,都写成2的多少次方即可。

小结

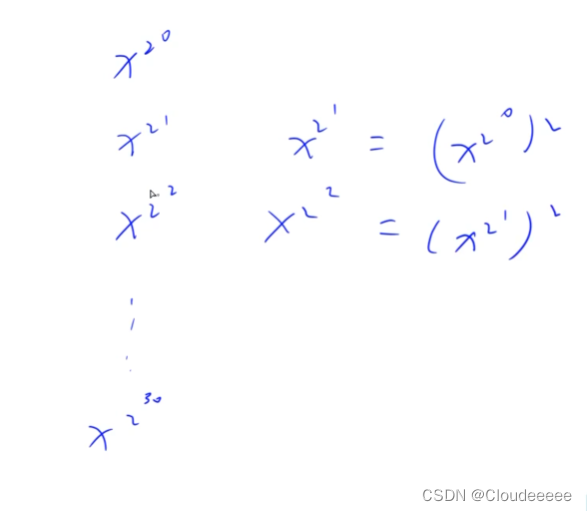
即每一个数是上一个数的平方。
看下面这个例子
先预处理出4的2的0次方到4的2的2次方
4的2的0次方是4
4的2的1次方是4的平方模10=6
4的2的2次方是上面结果6的平方模10,结果还是6
之后把4的5次方中的5拆成2进制形式
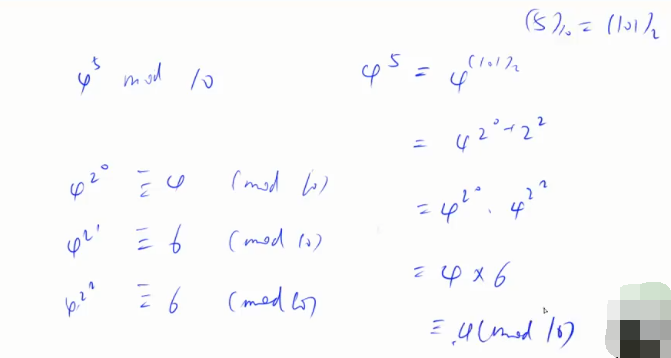

由于这里范围是10的9次方,有乘积int会报错,所以我们用long long
typedef long long LL;
//求a的k次方模p
int qmi(int a, int k, int p)
{
//若有4的5次方模10,这里的a相当于4,5相当于k只不过k要用二进制形式,p就是10
int res = 1;
while (k)
{
//这里要用k的二进制
if (k & 1) //判断二进制下,最后以为是不是1
res = (LL)res * a % p;
//第一项是a的2的0次方,其实就是a自己
/*先求4的2的0次方是4
再求4的2的1次方是4的平方模10 = 6
再求4的2的2次方是上面结果6的平方模10,结果还是6*/
k >>= 1;
a = (LL)a * a % p;//让a变为下一个,a的2的0次方,下一个就是a的2的一次方
/* 4的2的0次方,下一个就是4的2的1次方
* 4的2的1次方用完之后,变成4的2的2次方
*/
}
return res;
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int a, k, p;
scanf("%d %d %d", &a, &k, &p);
printf("%d\n", qmi(a, k, p));//a的k次方模p
}
return 0;
}快速幂求逆元
逆元的性质:
同余式
设有正整数m,a,b。若满足m|(a-b),即m能被(a-b)整除,则称a与b对m同余。记为:
a ≡ b (mod p) ,也可以记为 a = b + kp
费马小定理
如果p是一个质数,而整数a不是p的倍数,则有a^(p-1) ≡ 1 (mod p)
乘法逆元的定义(太长不看)
若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a × x (mod m),则称 x 为 b 的模 m 乘法逆元,记为 b^−1 (mod m)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,b^(m−2) 即为 b 的乘法逆元。
(看这里)简而言之:
找到一个x,使得b × x ≡ 1 (mod m),这个x,则称 x 为 b 的模 m 的乘法逆元。
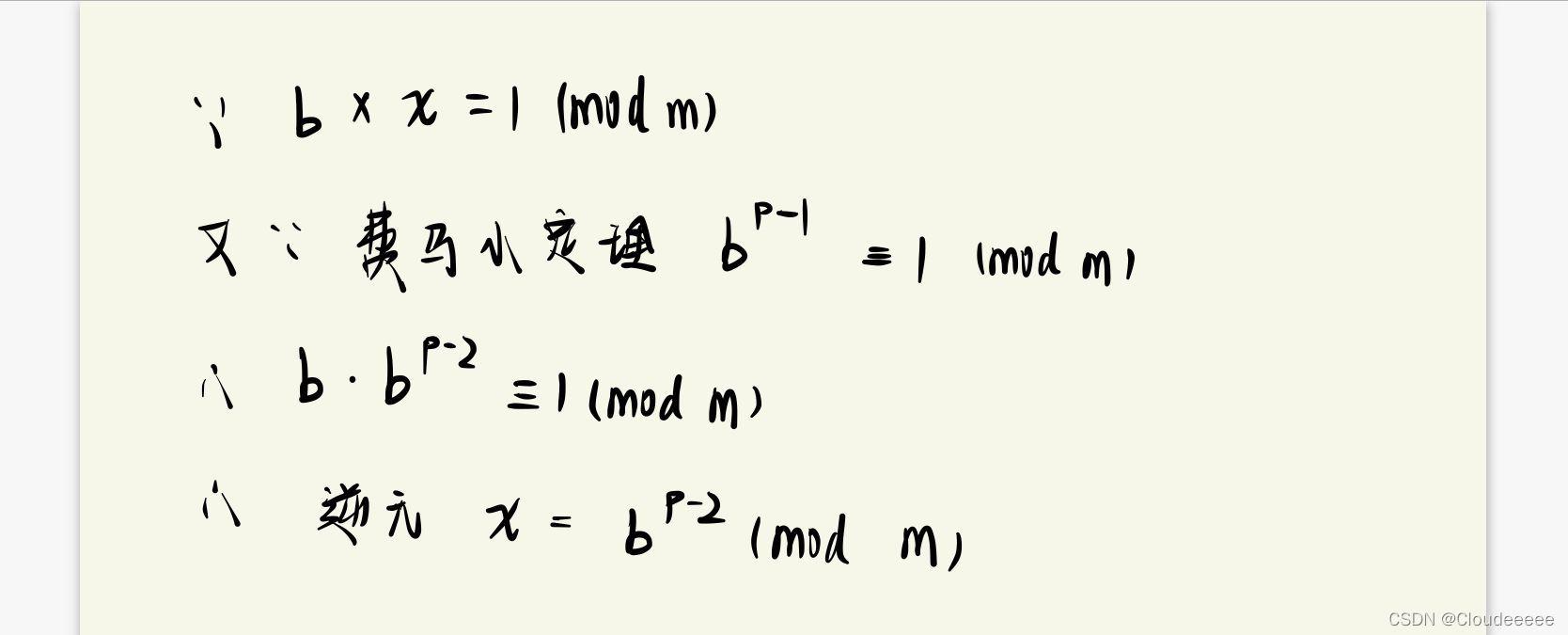
因此,求逆元就等同于求b的p-2次方模上m的结果,即快速幂。
typedef long long LL;
//求a的k次方模p
int qmi(int a, int k, int p)
{
//若有4的5次方模10,这里的a相当于4,5相当于k只不过k要用二进制形式,p就是10
int res = 1;
while (k)
{
//这里要用k的二进制
if (k & 1) //判断二进制下,最后以为是不是1
res = (LL)res * a % p;
//第一项是a的2的0次方,其实就是a自己
/*先求4的2的0次方是4
再求4的2的1次方是4的平方模10 = 6
再求4的2的2次方是上面结果6的平方模10,结果还是6*/
k >>= 1;
a = (LL)a * a % p;//让a变为下一个,a的2的0次方,下一个就是a的2的一次方
/* 4的2的0次方,下一个就是4的2的1次方
* 4的2的1次方用完之后,变成4的2的2次方
*/
}
return res;
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int a, p;
scanf("%d %d", &a, &p);
int res = qmi(a, p - 2, p);
if (a%p)
printf("%d\n", res);//a的k次方模p
else puts("impossible");
}
return 0;
}扩展欧几里得算法
裴蜀定理:有一对正整数a,b,一定存在非0整数x,y使得ax+by=(a,b)括号表示a和b的最大公约数,即ax+by=d,d一定是a,b的最大公约数的倍数。
当b为0时
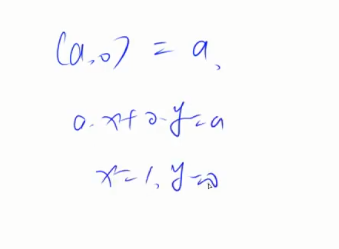

int exgcd(int a, int b, int& x, int& y)
{
if (!b)
{
x=1,y=0;
return a;
}
int d=exgcd(b, a % b,y,x);//注意这里x和y传参要翻转一下
y -= a / b * x;
return d;
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int a, b,x,y;
scanf("%d %d", &a, &b);
exgcd(a, b, x, y);//扩展欧几里得
printf("%d %d\n", x, y);
}
return 0;
}线性同余方程
使得(a*x)/m余数是b

第一个无解,第二个答案2,7都可以
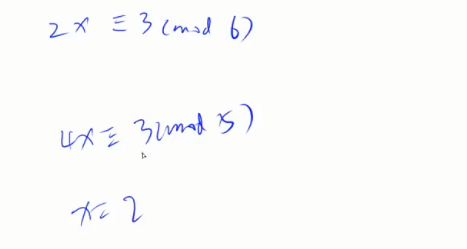
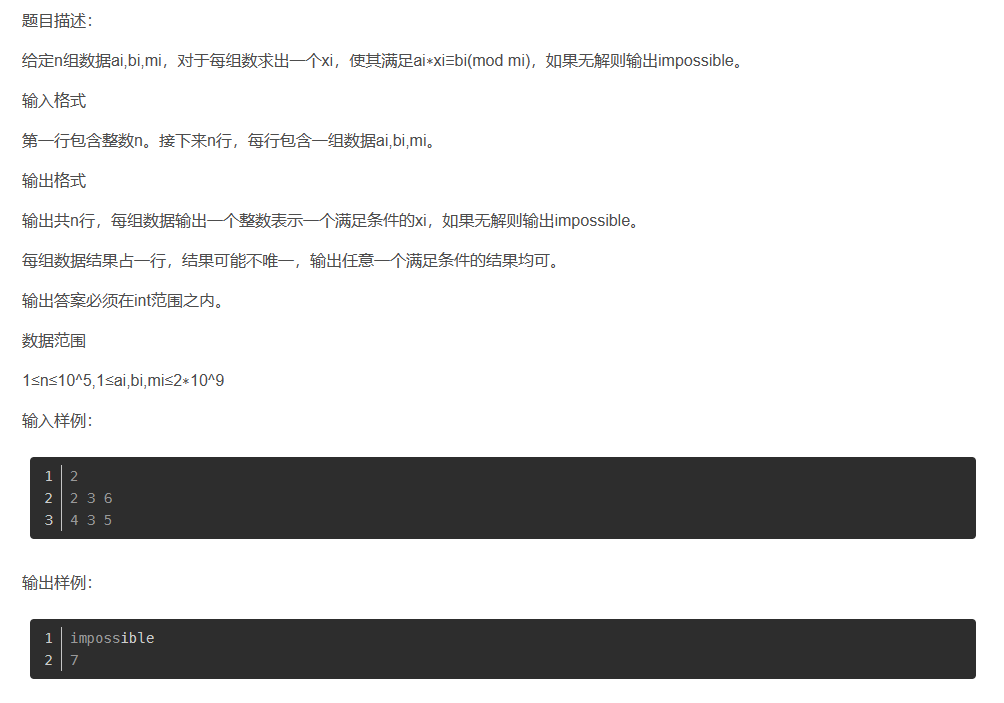
最顶部的方程有解,等价于最下面的等式有解,而这个等式有解的充分必要条件是,b必须整除a,m的最大公约数。

有解的重复必要条件

用扩展欧几里得算法求出x和y'算出d,d是最大公约数。
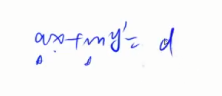
typedef long long LL;
int exgcd(int a, int b, int& x, int& y)
{
if (!b)
{
x=1,y=0;
return a;
}
int d=exgcd(b, a % b,y,x);//注意这里x和y传参要翻转一下
y -= a / b * x;
return d;
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int a, b,m;
scanf("%d %d %d", &a, &b,&m);
int x, y;
int d=exgcd(a, m, x,y);//扩展欧几里得
if (b % d) puts("impossible");//如果b不是d的倍数,一定无解
else printf("%d\n", (LL)x * (b / d) % m);
}
return 0;
}