1、排队模型

1. 排队：通常为了得到某种服务必须排队。有一类排队是有形的，例如在售票处等待买票的排队，加油站前汽车等待加油的排队等；还有一类排队是无形的，例如电话交换机接到的电话呼叫信号的排队，等待计算机中心处理机处理的信息的排队等。
2. 顾客：为了叙述的方便，排队者无论是人、物或信息，以后都统称为“顾客”。
3. 服务台：服务者无论是人或事物，例如一台电子计算机也可以是排队系统中的服务者，以后都统称为“服务台”，服务台用于服务队列中的顾客，可以多个服务台并发工作。
   

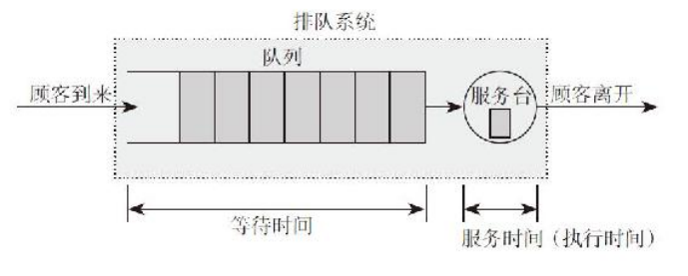
2、什么是排队论

• 排队论也称为随机服务系统理论、排队理论，是数学运筹学的分支学科。它是研究服务系统中排队现象随机规律的学科。排队论广泛应用于电信、交通工程、计算机网络、生产、运输、库存等各项资源共享的随机服务系统和工厂、商店、办公室、医院等的设计。
• 顾客总是希望服务机构越大越好，但是如果服务机构过大，人力和物力方面的开支就会相应地增加，从而就会造成浪费，因此研究排队模型的目的就是要在顾客需要和服务机构的规模之间进行权衡和决策，使其达到合理的平衡。
• 在计算机领域，许多软硬件组件都可以模型化为排队系统。我们可以使用排队理论分析排队现象，分析队列的长度、等待时间、利用率等指标。

3、李特尔法则（Little’s law）

3.1、李特尔法则的内容

1. 李特尔法则其实是一个公式，用来计算一个系统的平均请求数。
2. 李特尔法则可以用如下公式来表示：L=λW。即 平均访问请求数 = 平均到达速率 × 平均服务时间。比如，我们有一个系统，平均到达速率是10000次请求/s，每个请求需要花费0.05s来处理，即平均服务时间为0.05s，那么根据李特尔法则，服务器在任何时刻都将承担10000×0.05=500个请求的业务处理。

3.2、李特尔法则的意义

李特尔法则其实为我们改善服务器并发响应给出了思路：如果过了一段时间，由于客户端流量的上升，并发的访问速率达到了20000次请求/s，这种情况下，我们该如何改进系统的性能呢？根据李特尔法则，我们有如下两种方案：

• 提高服务器的并发处理能力，即20000×0.5=1000。
• 减少服务器的平均服务时间，即W=L/λ=500/20000=0.025s。

4、肯德尔排队表示法

4.1、肯德尔表示法的核心要素A/S/m

• 可以用肯德尔表示法来对排队系统进行分类，肯德尔表示法可使用如下的简化形式：A/S/m
  • A：到达的规则，即到达的时间间隔的分布，可能是随机的、确定型的或泊松分布等其他分布方式。
  • S：服务规则，即指服务时间的分布，可能是固定的或指数的等其他分布方式。
  • m：服务台个数，一个或多个。

4.2、肯德尔表示法中对顾客达到分布的表示：

• 表示顾客到达的间隔时间和服务时间的分布常用的约定符号分别如下。
  • M：指数分布，在概率论和统计学中，指数分布（Exponential Distribution）是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔，等等。
  • D：确定型（Determini stic）。
  • G：一般（General）服务时间的分布。

4.3、用肯德尔表示法表示的常见排队模型

一些常见的排队系统模型具体如下：

• M/M/1：表示顾客相继到达的间隔时间为指数分布、服务时间为指数分布、单服务台。
• M/M/c：表示顾客相继到达的间隔时间为指数分布、服务时间为指数分布、多服务台。
• M/G/1：表示顾客相继到达的间隔时间为指数分布、服务时间为一般服务时间分布、单服务台。
• M/D/1：表示顾客相继到达的间隔时间为指数分布、服务时间为确定型时间分布、单服务台。比如我们的旋转磁盘可用此模型进行分析。

5、总结

1. 用排队模型可以对MySQL等系统的性能进行建模，排队模型主要有顾客（排队者）和服务台（服务者）这两个核心要素。
2. 李特尔法则：平均请求数 = 平均到达速率 × 平均服务时间。根据李特尔法则，我们要想调节其中一个变量，就需要变动另外两个变量。
3. 可以用肯德尔表示法来表示常见排队模型，主要包括A/S/m三个要素，分别为到达规则、服务规则和服务台数量。