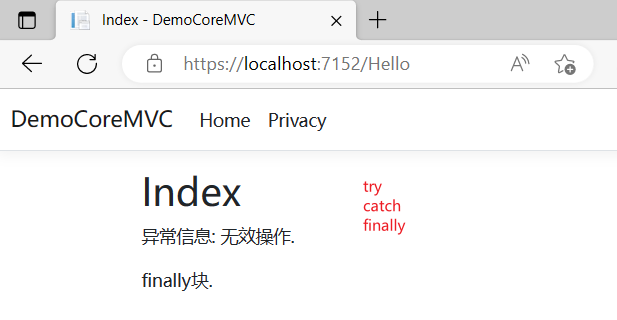
在时间序列分析中,相位轨迹也被广泛应用于提取隐藏在数据中的结构信息。例如,在人类活动识别任务中,通过构建不同活动对应的相位轨迹,可以揭示活动间的相似性和差异性,从而有助于设计有效的分类方法。
相空间(Phase Space)是一个用于描述动态系统状态的数学概念。在相空间中,一个系统的状态由一组变量(通常称为状态变量)表示,这些变量共同定义了系统在某一时刻的完整状态。相空间可以是有限维的(例如,二维或三维),也可以是无限维的。动态系统在相空间中的演化规律则由一组微分方程或差分方程来描述。
在相空间中,系统状态的轨迹称为相轨迹。相轨迹描绘了系统随时间演化的状态变化,表现为一条线或曲线。通过分析相轨迹,我们可以揭示动态系统的一些重要特性,如稳定性、周期性、混沌性等。
以下是一些相空间的关键概念:
-
状态变量:描述系统状态的变量。例如,在力学系统中,状态变量通常包括位置和速度;在电子电路中,状态变量可能包括电压和电流。
-
状态空间:由状态变量的所有可能取值组成的空间。状态空间的维度等于状态变量的数量。例如,一个有两个状态变量(位置和速度)的力学系统的状态空间是二维的。
-
相轨迹:系统状态在相空间中随时间演化的轨迹。相轨迹可以帮助我们理解系统的动态行为,如稳定性、周期性、混沌性等。
-
吸引子:在相空间中,系统演化过程中可能会趋向于某个集合的特征。这个集合称为吸引子。吸引子可以是一个点(固定点),一条线(周期轨迹)或更复杂的形状(如奇异吸引子,例如洛伦兹吸引子)。
-
初始条件敏感性:动态系统的相轨迹可能对初始条件非常敏感,这意味着即使初始条件的微小变化也可能导致系统状态演化出现显著差异。这种现象在混沌系统中尤为明显。
在时间序列分析和动态系统研究中,相空间是一个非常重要的概念。通过研究相空间和相轨迹,我们可以更好地理解系统的内在动力学行为,从而有助于设计有效的控制策略和预测方法。
生成相空间轨迹并进行可视化:
-
数据预处理:对加速度数据进行去噪、滤波、标准化等预处理操作,以消除噪声和非相关信息。
-
选择嵌入维数和延迟:使用启发式方法或信息论方法估计嵌入维数和时间延迟。例如,通过法肯斯均值定理(FNN)确定嵌入维数,使用互信息法确定时间延迟。
-
状态空间重构:根据所选的嵌入维数和时间延迟,将加速度数据转换为状态空间表示。给定加速度时间序列 a(t),构建一个 n 维状态向量 A(t) = [a(t), a(t + τ), a(t + 2τ), ..., a(t + (n-1)τ)],其中 n 是嵌入维数,τ 是时间延迟。
-
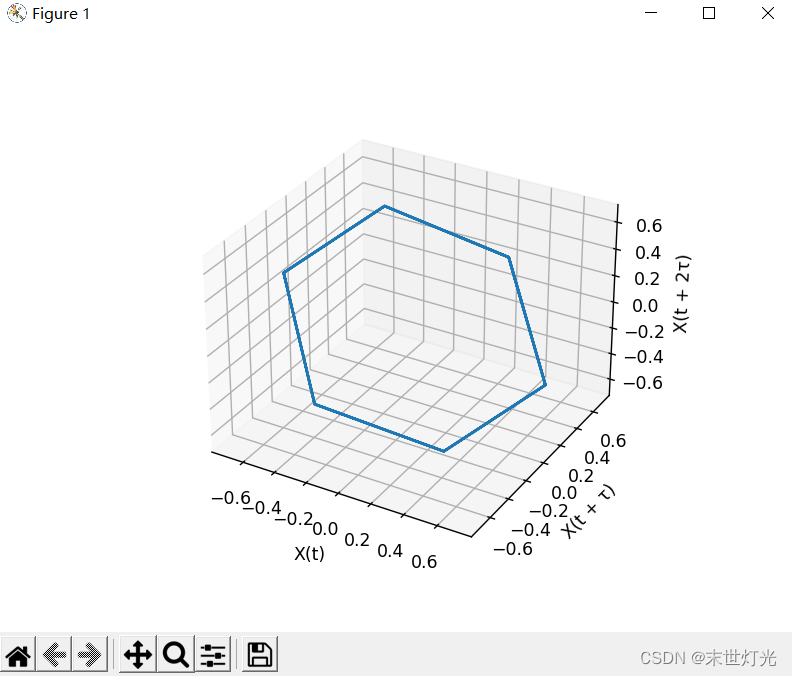
绘制相位轨迹:在状态空间中,将每个状态向量表示为一个点。根据数据的维度,您可以选择二维、三维或更高维的可视化方法。在Python中,可以使用matplotlib库进行绘图。
以下是一个使用matplotlib绘制三维相位轨迹的Python示例:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 加载加速度数据
accel_data = np.loadtxt('acceleration_data.txt')
# 假设已经确定了嵌入维数和时间延迟
embedding_dim = 3
time_delay = 5
# 状态空间重构
state_vectors = []
for i in range(len(accel_data) - (embedding_dim - 1) * time_delay):
state_vector = [accel_data[i + j * time_delay] for j in range(embedding_dim)]
state_vectors.append(state_vector)
state_vectors = np.array(state_vectors)
# 绘制三维相位轨迹
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(state_vectors[:, 0], state_vectors[:, 1], state_vectors[:, 2])
ax.set_xlabel('X(t)')
ax.set_ylabel('X(t + τ)')
ax.set_zlabel('X(t + 2τ)')
plt.show()
数据:
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0