一谈到 NLP,大家都听说过 Transformer, Self-attention 这些词汇,以及 Attension is all you need 这篇论文。 大家可能多多少少看过这类博客,对这些概念有一些了解,什么 QKV呀, encoder, decoder呀。我也看过,但是对 multiHeadAttention 一直以来都是迷迷糊糊的,主要是一些 shape 的变换把人搞懵了。本博客站在大家的肩膀上整理了下,描述这些概念的同时,加上 shape 的说明,让这些概念更清晰。最后用代码复现论文中的这些概念。
建议一边阅读本博客一边对着代码看,完整代码见最后。
Transformer
- 总揽
- Self-Attention
- 1. Scaled Dot-Product Attention
- 2.Q K V矩阵
- 3. d k \sqrt{d_k} dk的意义
- 4. 再谈Mask
- 5. 总结
- MultiHeadAttention
- FeedForwardNet
- 代码复现
- 最后的 Linear 和 Softmax
- 代码解读
- greed_search 编码
总揽
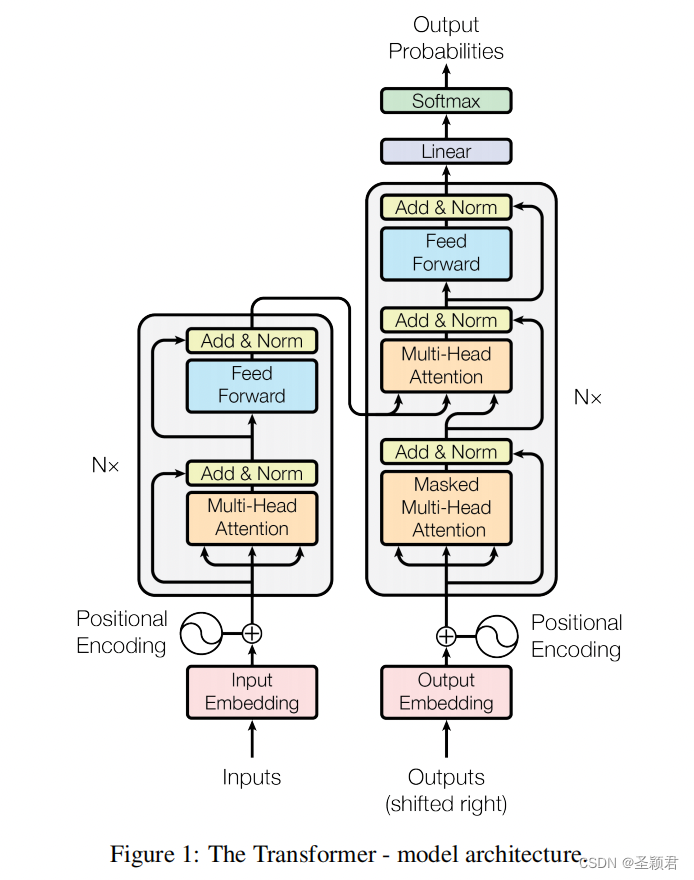

左边是 Encoder,
N
X
N_X
NX表示重复多次, 右边是 Decoder。
对于 Encoder, Inputs 表述输入的句子,embeding 之后加入位置信息(Positional Encoding 不需要学习)。 其 shape 为
X
_
e
m
b
e
d
=
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
d
_
m
o
d
e
l
]
;
d
_
m
o
d
e
l
=
e
m
b
e
d
_
d
i
m
X\_embed = [batch, seq\_len,d\_model]; d\_model = embed\_dim
X_embed=[batch,seq_len,d_model];d_model=embed_dim
Decoder 中每个 Layer 做两次 Attention,第一次可以称作 decoder_self_attention,第二次 decoder_encoder_attention,注意第二次 attention,KV 来自 encoder 的最后的输出。
Self-Attention
1. Scaled Dot-Product Attention
Self-Attention 是 Transformer最核心的思想, 一说到 self-attension(论文中也叫作 Scaled Dot-Product Attention), 大家脑海中都能想到一个图:
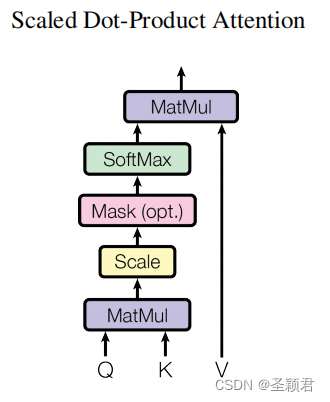
当不考虑图中的 Mask 时,该图对应的公式为:
S o f t m a x ( Q K T d k ) V Softmax(\frac{QK^T}{\sqrt{d_k}})V Softmax(dkQKT)V
首先, QKV 都是唬人的,对于Self-attention而言,暂时可以认为Q,K, V的输入源其实都是 embeding 之后的输入 X。
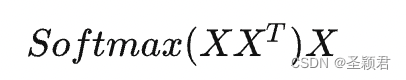
我们先抛开Q K V三个矩阵不谈,self-Attention最原始的形态其实长上面这样。那么这个公式到底是什么意思呢?
一个矩阵乘以它自己的转置,会得到什么结果,有什么意义?
向量的内积,其几何意义是什么?
答:表征两个向量的夹角,表征一个向量在另一个向量上的投影
记住这个知识点,我们进入一个超级详细的实例:
我们假设 ,其中 X = [ x 1 T ; x 2 T ; X 3 T ] X =[x_1^T; x_2^T;X_3^T] X=[x1T;x2T;X3T],其中 X X X 为一个二维矩阵, x i T x_i^T xiT为一个行向量(很多教材都默认向量是列向量,所以转置之后可以认为是行向量)。对应下面的图, x 1 T x_1^T x1T 对应"早"字embedding之后的结果,以此类推。
下面的运算模拟了一个过程,即
X
X
T
XX^T
XXT。我们来看看其结果究竟有什么意义
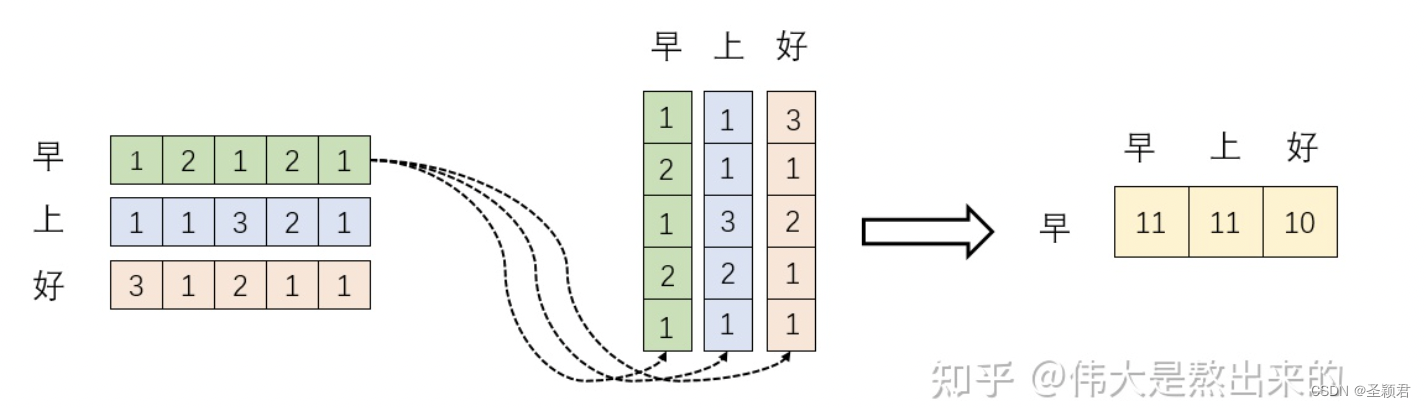
首先,行向量
x
i
T
x_i^T
xiT 分别与自己和其他两个行向量做内积(“早"分别与"上”"好"计算内积),得到了一个新的向量。我们回想前文提到的向量的内积表征两个向量的夹角,表征一个向量在另一个向量上的投影。那么新的向量向量有什么意义的?是行向量
x
i
T
x_i^T
xiT 在自己和其他两个行向量上的投影。我们思考,投影的值大有什么意思?投影的值小又如何?
投影的值大,说明两个向量相关度高。
我们考虑,如果两个向量夹角是九十度,那么这两个向量线性无关,完全没有相关性!
更进一步,这个向量是词向量,是词在高维空间的数值映射。词向量之间相关度高表示什么?是不是在一定程度上(不是完全)表示,在关注词A的时候,应当给予词B更多的关注?
上图展示了一个行向量运算的结果,那么矩阵 X X T XX^T XXT的意义是什么呢?
矩阵 X X T XX^T XXT是一个方阵,我们以行向量的角度理解,里面保存了每个向量与自己和其他向量进行内积运算的结果。
至此,我们理解了公式
S
o
f
t
m
a
x
(
X
X
T
)
X
Softmax(XX^T)X
Softmax(XXT)X 中
X
X
T
XX^T
XXT的意义。我们进一步,Softmax 的意义何在呢?请看下图
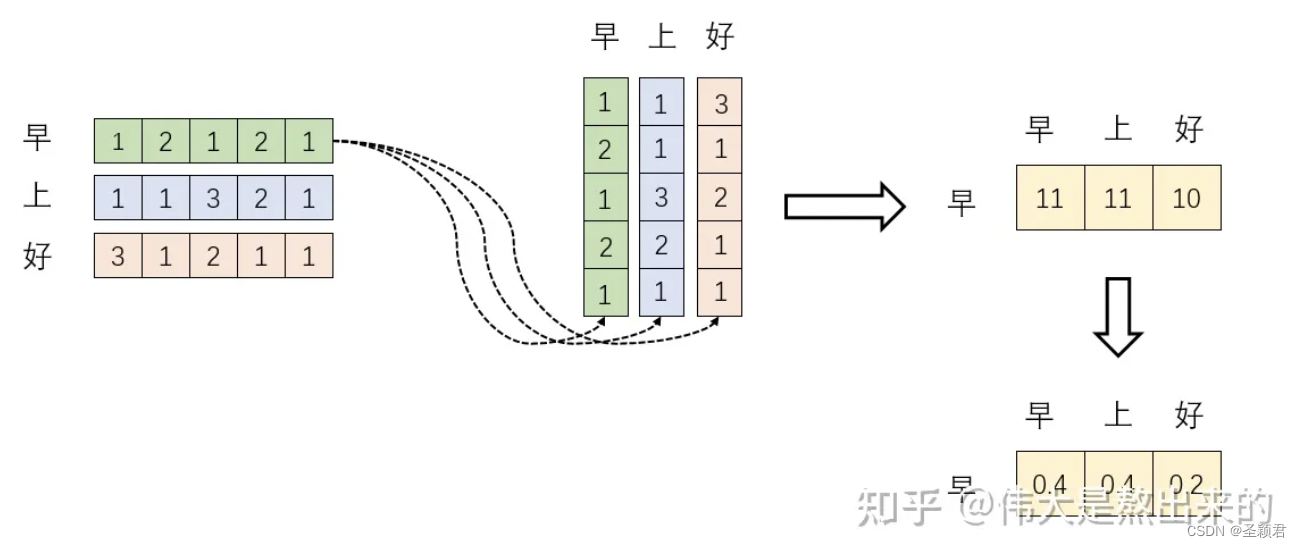
我们回想Softmax的公式,Softmax操作的意义是什么呢?
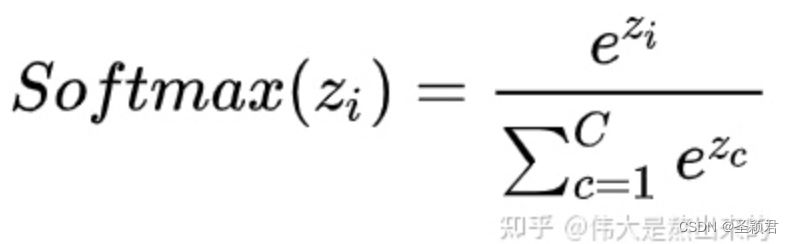
答:归一化
我们结合上面图理解,Softmax之后,这些数字的和为1了。我们再想,Attention机制的核心是什么?
加权求和
那么权重从何而来呢?就是这些归一化之后的数字。当我们关注"早"这个字的时候,我们应当分配0.4的注意力给它本身,剩下0.4关注"上",0.2关注"好"。当然具体到我们的Transformer,就是对应向量的运算了,这是后话。
我们仿佛已经拨开了一些迷雾,公式
S
o
f
t
m
a
x
(
X
X
T
)
X
Softmax(XX^T)X
Softmax(XXT)X 已经理解了其中的一半。最后一个 X 有什么意义?完整的公式究竟表示什么?我们继续之前的计算,请看下图

我们取
S
o
f
t
m
a
x
(
X
X
T
)
X
Softmax(XX^T)X
Softmax(XXT)X 的一个行向量举例。这一行向量与
X
X
X 的一个列向量相乘,表示什么?
观察上图,行向量与 X X X 的第一个列向量相乘,得到了一个新的行向量,且这个行向量与 X X X 的维度相同。
在新的向量中,每一个维度的数值都是由三个词向量在这一维度的数值加权求和得来的,这个新的行向量就是"早"字词向量经过注意力机制加权求和之后的表示。
如果您坚持阅读到这里,相信对公式 S o f t m a x ( X X T ) X Softmax(XX^T)X Softmax(XXT)X 已经有了更深刻的理解。
我们接下来解释原始公式中一些细枝末节的问题。
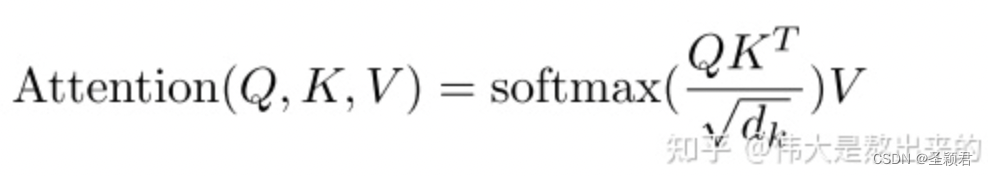
2.Q K V矩阵
在我们之前的例子中并没有出现Q K V的字眼,因为其并不是公式中最本质的内容。
Q K V究竟是什么?我们看下面的图

其实,许多文章中所谓的Q K V矩阵、查询向量之类的字眼,其来源是
X
X
X 与矩阵的乘积,本质上都是
X
X
X 的线性变换(映射)。
为什么不直接使用 X X X 而要对其进行线性变换(映射)?
当然是为了提升模型的拟合能力,矩阵 W W W 都是可以训练的,起到一个缓冲的效果。
如果你真正读懂了前文的内容,读懂了 S o f t m a x ( X X T ) X Softmax(XX^T)X Softmax(XXT)X 这个矩阵的意义,相信你也理解了所谓查询向量一类字眼的含义。
3. d k \sqrt{d_k} dk的意义

4. 再谈Mask
前面说过
Q
∗
K
T
Q*K^T
Q∗KT,可以理解为每个词之间的相关性,或者说词与词之间的 attention 得分,即
S
c
o
r
e
s
=
Q
∗
K
T
Scores = Q*K^T
Scores=Q∗KT。用图表示如下:

然后把这个 Scores 矩阵加上三角形的 Attention Mask,它将我们想要屏蔽的单元格设置为负无穷大或者一个非常大的负数。

然后对每一行使用 softmax, 会产生实际的注意力分数,然后使用这些分数进行加权求和。

这个分数表的函数如下:
- 当模型处理数据集中的第 1 个数据(第 1 行),其中只包含着一个单词(robut),它将 100 %的注意力集中在这个单词上。
- 当模型处理数据集中的第 2 个数据(第 2 行),其中只包含着单词(robut must),它将 42%的注意力集中在robot上,将57%的注意力集中在 must。
- 诸如此类,继续处理后面的单词。
5. 总结
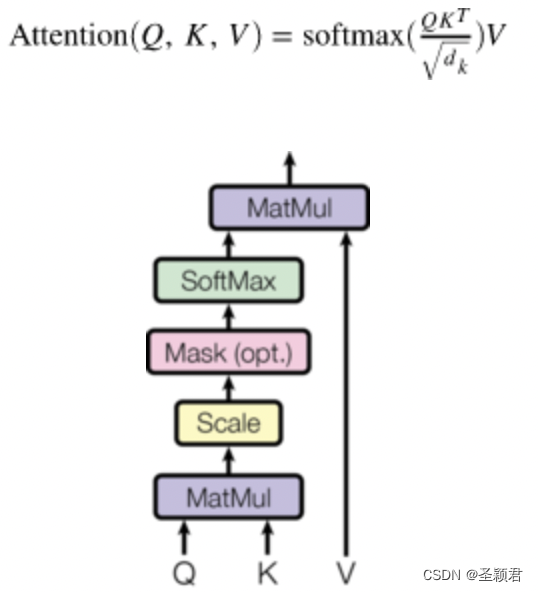
我们来看下 shape 的变化过程,也算是一个总结。
S
o
f
t
m
a
x
(
Q
K
T
d
k
)
V
Softmax(\frac{QK^T}{\sqrt{d_k}})V
Softmax(dkQKT)V
Q
:
[
b
a
t
c
h
,
q
u
e
r
y
_
l
e
n
,
d
_
q
]
Q : [batch, query\_len, d\_q]
Q:[batch,query_len,d_q]
K
:
[
b
a
t
c
h
,
k
e
y
_
l
e
n
,
d
_
k
]
K : [batch, key\_len, d\_k]
K:[batch,key_len,d_k]
V
:
[
b
a
t
c
h
,
v
a
l
u
e
_
l
e
n
,
d
_
v
]
V : [batch, value\_len, d\_v]
V:[batch,value_len,d_v]
k
e
y
_
l
e
n
key\_len
key_len =
v
a
l
u
e
_
l
e
n
value\_len
value_len
d
_
q
d\_q
d_q =
d
_
k
d\_k
d_k =
d
_
v
d\_v
d_v
O u t = Q ∗ K T ∗ V : [ b a t c h , q u e r y _ l e n , d _ v ] Out = Q*K^T*V: [batch, query\_len, d\_v] Out=Q∗KT∗V:[batch,query_len,d_v]
可以看出, 最后的输出 Out 和 Q 的 shape 一致
对于实际场景(如Encoder):
X
_
e
m
b
e
d
:
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
d
_
m
o
d
e
l
]
X\_embed : [batch, seq\_len, d\_model]
X_embed:[batch,seq_len,d_model],
d
_
m
o
d
e
l
d\_model
d_model 为 embeding size
Q
K
V
QKV
QKV 是
X
X
X 线性变换后得到的:
W
Q
=
[
d
_
m
o
d
e
l
,
d
_
q
]
W^Q= [d\_model, d\_q]
WQ=[d_model,d_q]
W
K
=
[
d
_
m
o
d
e
l
,
d
_
k
]
W^K= [d\_model, d\_k]
WK=[d_model,d_k]
W
V
=
[
d
_
m
o
d
e
l
,
d
_
v
]
W^V= [d\_model, d\_v]
WV=[d_model,d_v]
Q
=
X
_
e
m
b
e
d
∗
W
Q
:
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
d
_
q
]
Q = X\_embed * W^Q: [batch, seq\_len, d\_q]
Q=X_embed∗WQ:[batch,seq_len,d_q]
K
=
X
_
e
m
b
e
d
∗
W
K
:
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
d
_
k
]
K = X\_embed * W^K: [batch, seq\_len, d\_k]
K=X_embed∗WK:[batch,seq_len,d_k]
V
=
X
_
e
m
b
e
d
∗
W
V
:
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
d
_
v
]
V = X\_embed * W^V: [batch, seq\_len, d\_v]
V=X_embed∗WV:[batch,seq_len,d_v]
MultiHeadAttention
上面 Scaled Dot-Product Attention 相信大多数人都能理解,大多数博客都是重点介绍 Scaled Dot-Product Attention, 对于 MultiHeadAttention 都解释得一笔带过,看着始终有点迷糊,我们先不用看论文里面那个图,先自己回想一下。
回想一下,大致的意思是,多头就是多个空间,Q K V 的shape 变为:
Q
:
[
b
a
t
c
h
,
q
u
e
r
y
_
l
e
n
,
n
_
h
e
a
d
s
∗
d
_
q
]
Q : [batch, query\_len, n\_heads * d\_q]
Q:[batch,query_len,n_heads∗d_q]
K
:
[
b
a
t
c
h
,
k
e
y
_
l
e
n
,
n
_
h
e
a
d
s
∗
d
_
k
]
K : [batch, key\_len, n\_heads * d\_k]
K:[batch,key_len,n_heads∗d_k]
V
:
[
b
a
t
c
h
,
v
a
l
u
e
_
l
e
n
,
n
_
h
e
a
d
s
∗
d
_
v
]
V : [batch, value\_len, n\_heads * d\_v]
V:[batch,value_len,n_heads∗d_v]
对于 Encoder 的输入
X
_
e
m
b
e
d
:
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
d
_
m
o
d
e
l
]
X\_embed: [batch, seq\_len, d\_model]
X_embed:[batch,seq_len,d_model]
W
Q
=
[
d
_
m
o
d
e
l
,
n
_
h
e
a
d
s
∗
d
_
q
]
W^Q= [d\_model, n\_heads * d\_q]
WQ=[d_model,n_heads∗d_q]
W
K
=
[
d
_
m
o
d
e
l
,
n
_
h
e
a
d
s
∗
d
_
k
]
W^K= [d\_model, n\_heads * d\_k]
WK=[d_model,n_heads∗d_k]
W
V
=
[
d
_
m
o
d
e
l
,
n
_
h
e
a
d
s
∗
d
_
v
]
W^V= [d\_model, n\_heads * d\_v]
WV=[d_model,n_heads∗d_v]
映射输入 X X X(计算 Q K V QKV QKV)
Q
=
X
∗
W
Q
=
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
n
_
h
e
a
d
s
∗
d
_
q
]
−
−
−
拆成多头
>
[
b
a
t
c
h
,
s
e
q
_
l
e
n
,
n
_
h
e
a
d
s
,
d
_
q
]
−
−
−
r
e
s
h
a
p
e
>
[
b
a
t
c
h
,
n
_
h
e
a
d
s
,
s
e
q
_
l
e
n
,
d
_
q
]
Q = X * W^Q = [batch, seq\_len, n\_heads * d\_q] ---拆成多头> [batch, seq\_len, n\_heads, d\_q] ---reshape> [batch, n\_heads, seq\_len, d\_q]
Q=X∗WQ=[batch,seq_len,n_heads∗d_q]−−−拆成多头>[batch,seq_len,n_heads,d_q]−−−reshape>[batch,n_heads,seq_len,d_q]
K
V
KV
KV的计算方式一样
计算self-attention
此时
S
o
f
t
m
a
x
(
Q
K
T
d
k
)
V
Softmax(\frac{QK^T}{\sqrt{d_k}})V
Softmax(dkQKT)V 的计算shape 为:
O
u
t
1
=
Q
∗
K
T
=
[
b
a
t
c
h
,
n
_
h
e
a
d
s
,
s
e
q
_
l
e
n
,
s
e
q
_
l
e
n
]
Out_1 = Q*K^T = [batch,n\_heads,seq\_len,seq\_len]
Out1=Q∗KT=[batch,n_heads,seq_len,seq_len]
C
o
n
t
e
x
t
=
O
u
t
1
∗
V
=
[
b
a
t
c
h
,
n
_
h
e
a
d
s
,
s
e
q
_
l
e
n
,
d
_
v
]
Context = Out_1 * V = [batch,n\_heads,seq\_len,d\_v]
Context=Out1∗V=[batch,n_heads,seq_len,d_v]
将不同头的输出向量拼接在一起(Concat)
C o n t e x t = [ b a t c h , s e q _ l e n , n _ h e a d s ∗ d _ v ] Context = [batch,seq\_len,n\_heads * d\_v] Context=[batch,seq_len,n_heads∗d_v]
然后通过一个全连接层,保证多头attention的输出仍然是seq_len x d_model
L i n e a r = ( n _ h e a d s ∗ d _ v , d _ m o d e l ) Linear = (n\_heads * d\_v, d\_model) Linear=(n_heads∗d_v,d_model)
O u t p u t = C o n t e x t ∗ L i n e r = [ b a t c h , s e q _ l e n , d _ m o d e l ] Output = Context* Liner = [batch,seq\_len,d\_model] Output=Context∗Liner=[batch,seq_len,d_model]
OK, 现在上一个图:
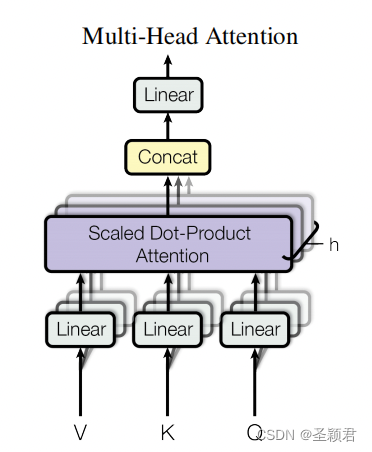
这个图中的
Q
K
V
QKV
QKV,其实是输入
X
X
X,或者理解为“映射之前的QKV”,我觉得这个映射之前的说法是准确的。
与最开始 Scaled Dot-Product Attention 中的
Q
K
V
QKV
QKV有些不同。即一个是映射之后的
Q
K
V
QKV
QKV, 一个是映射之前的
Q
K
V
QKV
QKV,即
X
X
X。
从 Scaled Dot-Product Attention 和 MultiHeadAttention 的图中也可以看出这种区别,一个
Q
K
V
QKV
QKV之后有 Linear(映射),一个没有。
FeedForwardNet
Feed Forward 层比较简单,是一个两层的全连接层,第一层的激活函数为 Relu,第二层不使用激活函数。
代码复现
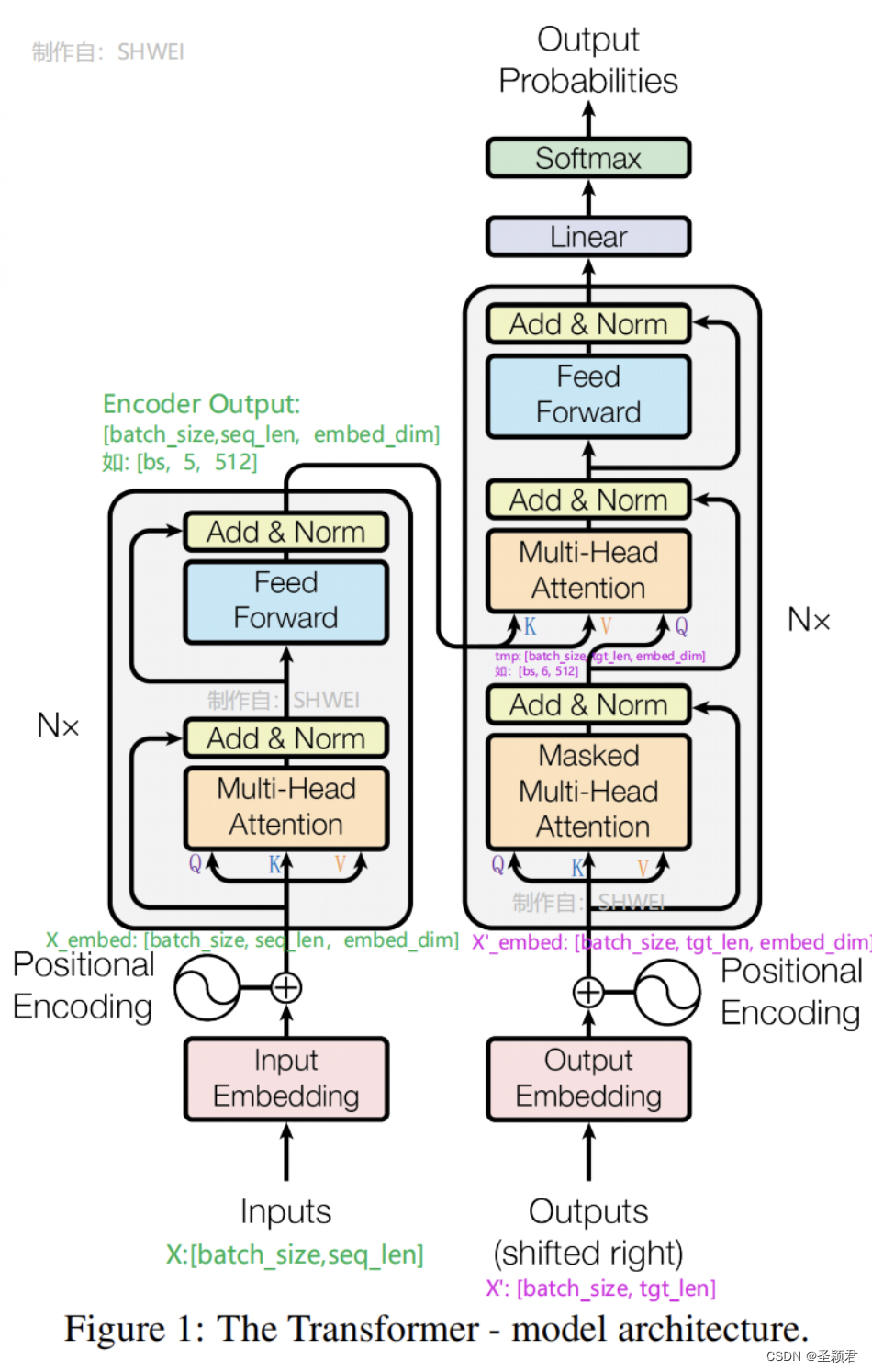
现在完全遵照这幅图的架构,组网一个 transformer 模型。注意一共有三个 Multi-Head Attention,注意 Decoder 中的第一个 Multi-Head Attention 是有 mask 的。
Encoder 最后需要经过一个 Linear 和 Softmax
最后的 Linear 和 Softmax
Encoder 的输出shape 为
e
n
c
o
d
e
r
_
o
u
t
:
[
b
a
t
c
h
_
s
i
z
e
,
t
g
t
_
l
e
n
,
d
_
m
o
d
e
l
]
encoder\_out :[batch\_size, tgt\_len,d\_model]
encoder_out:[batch_size,tgt_len,d_model]
n
n
.
L
i
n
e
a
r
(
d
_
m
o
d
e
l
,
t
g
t
_
v
o
c
a
b
_
s
i
z
e
)
nn.Linear(d\_model, tgt\_vocab\_size)
nn.Linear(d_model,tgt_vocab_size)
所以最后的输出shape为:
o
u
t
:
[
b
a
t
c
h
_
s
i
z
e
,
t
g
t
_
l
e
n
,
t
g
t
_
v
o
c
a
b
_
s
i
z
e
]
out :[batch\_size, tgt\_len,tgt\_vocab\_size]
out:[batch_size,tgt_len,tgt_vocab_size]
假设
b
a
t
c
h
_
s
i
z
e
=
1
,
t
g
t
_
l
e
n
=
4
batch\_size = 1,tgt\_len=4
batch_size=1,tgt_len=4, 词表长度
t
g
t
_
v
o
c
a
b
_
s
i
z
e
=
6
tgt\_vocab\_size=6
tgt_vocab_size=6
经过 softmax,得到的每个位置上的 tocken 在词表上的概率分布。

代码解读
模型组网代码:
# ====================================================================================================
# Transformer模型
# 位置编码,无需学习
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0).transpose(0, 1)
self.register_buffer('pe', pe)
def forward(self, x):
"""
x: [seq_len, batch_size, d_model]
"""
x = x + self.pe[:x.size(0), :]
return self.dropout(x)
def get_attn_mask(seq):
"""建议打印出来看看是什么的输出(一目了然)
seq: [batch_size, tgt_len]
"""
attn_shape = [seq.size(0), seq.size(1), seq.size(1)]
# attn_shape: [batch_size, tgt_len, tgt_len]
subsequence_mask = np.triu(np.ones(attn_shape), k=1) # 生成一个上三角矩阵
subsequence_mask = torch.from_numpy(subsequence_mask).bool()
return subsequence_mask # [batch_size, tgt_len, tgt_len]
class ScaledDotProductAttention(nn.Module):
def __init__(self):
super(ScaledDotProductAttention, self).__init__()
def forward(self, Q, K, V, attn_mask = None):
"""
Q: [batch_size, n_heads, len_q, d_k]
K: [batch_size, n_heads, len_k, d_k]
V: [batch_size, n_heads, len_v(=len_k), d_v]
attn_mask: [batch_size, n_heads, seq_len, seq_len]
说明: 在encoder-decoder的Attention层中 len_q 和 len_k 可能不同
"""
scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k) # scores : [batch_size, n_heads, len_q, len_k]
# mask矩阵填充scores(用-1e9填充scores中与attn_mask中值为1位置相对应的元素)
if(attn_mask is not None):
scores.masked_fill_(attn_mask, -1e9) # Fills elements of self tensor with value where mask is True.
attn = nn.Softmax(dim=-1)(scores) # 对最后一个维度(v)做softmax
# scores : [batch_size, n_heads, len_q, len_k] * V: [batch_size, n_heads, len_v(=len_k), d_v]
context = torch.matmul(attn, V) # context: [batch_size, n_heads, len_q, d_v]
return context
class MultiHeadAttention(nn.Module):
"""这个Attention类可以实现:
Encoder的Self-Attention
Decoder的Masked Self-Attention
Encoder-Decoder的Attention
输入:seq_len x d_model
输出:seq_len x d_model
"""
def __init__(self):
super(MultiHeadAttention, self).__init__()
self.W_Q = nn.Linear(d_model, d_k * n_heads, bias=False) # q,k必须维度相同,不然无法做点积
self.W_K = nn.Linear(d_model, d_k * n_heads, bias=False)
self.W_V = nn.Linear(d_model, d_v * n_heads, bias=False)
# 这个全连接层可以保证多头attention的输出仍然是seq_len x d_model
self.fc = nn.Linear(n_heads * d_v, d_model, bias=False)
def forward(self, input_Q, input_K, input_V, attn_mask = None):
"""
input_Q: [batch_size, len_q, d_model]
input_K: [batch_size, len_k, d_model]
input_V: [batch_size, len_v(=len_k), d_model]
"""
residual, batch_size = input_Q, input_Q.size(0)
# 下面的多头的参数矩阵是放在一起做线性变换的,然后再拆成多个头,这是工程实现的技巧
# B: batch_size, S:seq_len
# (B, S, d_model) -proj-> (B, S, d_k * n_heads) -split-> (B, S, n_heads, d_k) -trans-> (B, n_heads, S, d_k)
# 线性变换 拆成多头
# 计算 Q K V
# Q: [batch_size, n_heads, len_q, d_k]
Q = self.W_Q(input_Q).view(batch_size, -1, n_heads, d_k).transpose(1, 2)
# K: [batch_size, n_heads, len_k, d_k] # K和V的长度一定相同,维度可以不同
K = self.W_K(input_K).view(batch_size, -1, n_heads, d_k).transpose(1, 2)
# V: [batch_size, n_heads, len_v(=len_k), d_v]
V = self.W_V(input_V).view(batch_size, -1, n_heads, d_v).transpose(1, 2)
# 因为是多头,所以mask矩阵要扩充成4维的
# attn_mask: [batch_size, len_q, len_k] -> [batch_size, n_heads, len_q, len_k]
if(attn_mask is not None):
attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1)
# context: [batch_size, n_heads, len_q, d_v], attn: [batch_size, n_heads, len_q, len_k]
context = ScaledDotProductAttention()(Q, K, V, attn_mask)
# 下面将不同头的输出向量拼接在一起
# context: [batch_size, n_heads, len_q, d_v] -> [batch_size, len_q, n_heads * d_v]
context = context.transpose(1, 2).reshape(batch_size, -1, n_heads * d_v)
# 这个全连接层可以保证多头attention的输出仍然是len_q x d_model
output = self.fc(context) # [batch_size, len_q, d_model]
return nn.LayerNorm(d_model).to(device)(output + residual)
# Pytorch中的Linear只会对最后一维操作,所以正好是我们希望的每个位置用同一个全连接网络
class PoswiseFeedForwardNet(nn.Module):
def __init__(self):
super(PoswiseFeedForwardNet, self).__init__()
self.fc = nn.Sequential(
nn.Linear(d_model, d_ff, bias=False),
nn.ReLU(),
nn.Linear(d_ff, d_model, bias=False)
)
def forward(self, inputs):
"""
inputs: [batch_size, seq_len, d_model]
"""
residual = inputs
output = self.fc(inputs)
return nn.LayerNorm(d_model).to(device)(output + residual) # [batch_size, seq_len, d_model]
class EncoderLayer(nn.Module):
def __init__(self):
super(EncoderLayer, self).__init__()
self.enc_self_attn = MultiHeadAttention()
self.pos_ffn = PoswiseFeedForwardNet()
def forward(self, enc_inputs):
"""E
enc_inputs: [batch_size, src_len, d_model]
"""
# enc_outputs: [batch_size, src_len, d_model]
# 第一个enc_inputs * W_Q = Q
# 第二个enc_inputs * W_K = K
# 第三个enc_inputs * W_V = V
enc_outputs = self.enc_self_attn(enc_inputs, enc_inputs, enc_inputs) # enc_inputs to same Q,K,V(未线性变换前)
enc_outputs = self.pos_ffn(enc_outputs)
# enc_outputs: [batch_size, src_len, d_model]
return enc_outputs
class DecoderLayer(nn.Module):
def __init__(self):
super(DecoderLayer, self).__init__()
self.dec_self_attn = MultiHeadAttention()
self.dec_enc_attn = MultiHeadAttention()
self.pos_ffn = PoswiseFeedForwardNet()
def forward(self, dec_inputs, enc_outputs, dec_self_attn_mask):
"""
dec_inputs: [batch_size, tgt_len, d_model]
enc_outputs: [batch_size, src_len, d_model]
dec_self_attn_mask: [batch_size, tgt_len, tgt_len]
"""
# dec_outputs: [batch_size, tgt_len, d_model]
dec_outputs = self.dec_self_attn(dec_inputs, dec_inputs, dec_inputs,
dec_self_attn_mask) # 这里的Q,K,V全是Decoder自己的输入
# dec_outputs: [batch_size, tgt_len, d_model]
dec_outputs = self.dec_enc_attn(dec_outputs, enc_outputs, enc_outputs) # Attention层的Q(来自decoder) 和 K,V(来自encoder)
dec_outputs = self.pos_ffn(dec_outputs) # [batch_size, tgt_len, d_model]
return dec_outputs
class Encoder(nn.Module):
def __init__(self):
super(Encoder, self).__init__()
self.src_emb = nn.Embedding(src_vocab_size, d_model) # token Embedding
self.pos_emb = PositionalEncoding(d_model) # Transformer中位置编码时固定的,不需要学习
self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)])
def forward(self, enc_inputs):
"""
enc_inputs: [batch_size, src_len]
"""
enc_outputs = self.src_emb(enc_inputs) # [batch_size, src_len, d_model]
enc_outputs = self.pos_emb(enc_outputs.transpose(0, 1)).transpose(0, 1) # [batch_size, src_len, d_model]
for layer in self.layers: # for循环访问nn.ModuleList对象
# 上一个layer的输出enc_outputs作为当前layer的输入
# enc_outputs: [batch_size, src_len, d_model]
enc_outputs = layer(enc_outputs)
return enc_outputs
class Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
self.tgt_emb = nn.Embedding(tgt_vocab_size, d_model) # Decoder输入的embed词表
self.pos_emb = PositionalEncoding(d_model)
self.layers = nn.ModuleList([DecoderLayer() for _ in range(n_layers)]) # Decoder的blocks
def forward(self, dec_inputs, enc_outputs):
"""
dec_inputs: [batch_size, tgt_len]
enc_outputs: [batch_size, src_len, d_model] # 用在Encoder-Decoder Attention层
"""
dec_outputs = self.tgt_emb(dec_inputs) # [batch_size, tgt_len, d_model]
dec_outputs = self.pos_emb(dec_outputs.transpose(0, 1)).transpose(0, 1).to(
device) # [batch_size, tgt_len, d_model]
# Decoder输入序列的 mask 矩阵
dec_self_attn_mask = get_attn_mask(dec_inputs).to(device) # [batch_size, tgt_len, tgt_len]
for layer in self.layers:
# dec_outputs: [batch_size, tgt_len, d_model]
# Decoder的当前 layer 的输入是上一个 layer 的输出dec_outputs(变化)和Encoder网络的输出enc_outputs(固定)
dec_outputs = layer(dec_outputs, enc_outputs, dec_self_attn_mask)
# dec_outputs: [batch_size, tgt_len, d_model]
return dec_outputs
class Transformer(nn.Module):
def __init__(self):
super(Transformer, self).__init__()
self.encoder = Encoder().to(device)
self.decoder = Decoder().to(device)
self.projection = nn.Linear(d_model, tgt_vocab_size, bias=False).to(device)
def forward(self, enc_inputs, dec_inputs):
"""Transformers的输入:两个序列
enc_inputs: [batch_size, src_len]
dec_inputs: [batch_size, tgt_len]
"""
# tensor to store decoder outputs
# outputs = torch.zeros(batch_size, tgt_len, tgt_vocab_size).to(self.device)
# enc_outputs: [batch_size, src_len, d_model]
# 经过Encoder网络后,得到的输出还是[batch_size, src_len, d_model]
enc_outputs = self.encoder(enc_inputs)
# dec_outputs: [batch_size, tgt_len, d_model]
dec_outputs = self.decoder(dec_inputs, enc_outputs)
# dec_outputs: [batch_size, tgt_len, d_model] -> dec_logits: [batch_size, tgt_len, tgt_vocab_size]
dec_logits = self.projection(dec_outputs)
return dec_logits.view(-1, dec_logits.size(-1))
训练:
# ====================================================================================================
# 数据构建
import math
import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim
import torch.utils.data as Data
device = 'cpu'
# device = 'cuda'
# transformer epochs
epochs = 100
# epochs = 1000
# 这里我没有用什么大型的数据集,而是手动输入了两对中文→英语的句子
# 还有每个字的索引也是我手动硬编码上去的,主要是为了降低代码阅读难度
# S: Symbol that shows starting of decoding input
# E: Symbol that shows ending of decoding output
# P: Symbol that will fill in blank sequence if current batch data size is short than time steps
# 训练集
sentences = [
# 中文和英语的单词个数不要求相同
# enc_input dec_input dec_output
['我 有 一 个 好 朋 友 P', 'S i have a good friend .', 'i have a good friend . E'],
['我 有 零 个 女 朋 友 P', 'S i have zero girl friend .', 'i have zero girl friend . E']
]
# 测试集(希望transformer能达到的效果)
# 输入:"我 有 一 个 女 朋 友"
# 输出:"i have a girlfriend"
# 中文和英语的单词要分开建立词库
# Padding Should be Zero
src_vocab = {'P': 0, '我': 1, '有': 2, '一': 3, '个': 4, '好': 5, '朋': 6, '友': 7, '零': 8, '女': 9}
src_idx2word = {i: w for i, w in enumerate(src_vocab)}
src_vocab_size = len(src_vocab)
tgt_vocab = {'P': 0, 'i': 1, 'have': 2, 'a': 3, 'good': 4, 'friend': 5, 'zero': 6, 'girl': 7, 'S': 8, 'E': 9, '.': 10}
idx2word = {i: w for i, w in enumerate(tgt_vocab)}
tgt_vocab_size = len(tgt_vocab)
src_len = 8 # (源句子的长度)enc_input max sequence length
tgt_len = 7 # dec_input(=dec_output) max sequence length
# Transformer Parameters
d_model = 512 # Embedding Size(token embedding和position编码的维度)
d_ff = 2048 # FeedForward dimension (两次线性层中的隐藏层 512->2048->512,线性层是用来做特征提取的),当然最后会再接一个projection层
d_k = d_v = 64 # dimension of K(=Q), V(Q和K的维度需要相同,这里为了方便让K=V)
n_layers = 6 # number of Encoder of Decoder Layer(Block的个数)
n_heads = 8 # number of heads in Multi-Head Attention(有几套头)
def make_data(sentences):
"""把单词序列转换为数字序列"""
enc_inputs, dec_inputs, dec_outputs = [], [], []
for i in range(len(sentences)):
enc_input = [[src_vocab[n] for n in sentences[i][0].split()]] # [[1, 2, 3, 4, 0], [1, 2, 3, 5, 0]]
dec_input = [[tgt_vocab[n] for n in sentences[i][1].split()]] # [[6, 1, 2, 3, 4, 8], [6, 1, 2, 3, 5, 8]]
dec_output = [[tgt_vocab[n] for n in sentences[i][2].split()]] # [[1, 2, 3, 4, 8, 7], [1, 2, 3, 5, 8, 7]]
enc_inputs.extend(enc_input)
dec_inputs.extend(dec_input)
dec_outputs.extend(dec_output)
return torch.LongTensor(enc_inputs), torch.LongTensor(dec_inputs), torch.LongTensor(dec_outputs)
enc_inputs, dec_inputs, dec_outputs = make_data(sentences)
class MyDataSet(Data.Dataset):
"""自定义DataLoader"""
def __init__(self, enc_inputs, dec_inputs, dec_outputs):
super(MyDataSet, self).__init__()
self.enc_inputs = enc_inputs
self.dec_inputs = dec_inputs
self.dec_outputs = dec_outputs
def __len__(self):
return self.enc_inputs.shape[0]
def __getitem__(self, idx):
return self.enc_inputs[idx], self.dec_inputs[idx], self.dec_outputs[idx]
loader = Data.DataLoader(MyDataSet(enc_inputs, dec_inputs, dec_outputs), 2, True)
# ==========================================================================================
# 训练
model = Transformer().to(device)
# 这里的损失函数里面设置了一个参数 ignore_index=0,因为 "pad" 这个单词的索引为 0,这样设置以后,就不会计算 "pad" 的损失(因为本来 "pad" 也没有意义,不需要计算)
criterion = nn.CrossEntropyLoss(ignore_index=0)
optimizer = optim.SGD(model.parameters(), lr=1e-3, momentum=0.99) # 用adam的话效果不好
for epoch in range(epochs):
for enc_inputs, dec_inputs, dec_outputs in loader:
"""
enc_inputs: [batch_size, src_len]
dec_inputs: [batch_size, tgt_len]
dec_outputs: [batch_size, tgt_len]
"""
enc_inputs, dec_inputs, dec_outputs = enc_inputs.to(device), dec_inputs.to(device), dec_outputs.to(device)
# outputs: [batch_size * tgt_len, tgt_vocab_size]
outputs = model(enc_inputs, dec_inputs)
loss = criterion(outputs, dec_outputs.view(-1)) # dec_outputs.view(-1):[batch_size * tgt_len * tgt_vocab_size]
print('Epoch:', '%04d' % (epoch + 1), 'loss =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
greed_search 编码
# ==========================================================================================
# 预测阶段
def greedy_decoder(model, enc_input, start_symbol):
"""贪心编码
For simplicity, a Greedy Decoder is Beam search when K=1. This is necessary for inference as we don't know the
target sequence input. Therefore we try to generate the target input word by word, then feed it into the transformer.
:param model: Transformer Model
:param enc_input: The encoder input
:param start_symbol: The start symbol. In this example it is 'S' which corresponds to index 8
:return: The target input
"""
enc_outputs = model.encoder(enc_input)
dec_input = torch.zeros(1, 0).type_as(enc_input.data) # 初始化一个空的tensor: tensor([], size=(1, 0), dtype=torch.int64)
terminal = False
next_symbol = start_symbol
while not terminal:
# 预测阶段:dec_input序列会一点点变长(每次添加一个新预测出来的单词)
dec_input = torch.cat([dec_input.to(device), torch.tensor([[next_symbol]], dtype=enc_input.dtype).to(device)],
-1)
# print("dec_input: ", dec_input)
dec_outputs = model.decoder(dec_input, enc_outputs)
projected = model.projection(dec_outputs)
print("projected: ", projected)
print("projected: ", projected.squeeze(0).max(dim=-1, keepdim=False))
prob = projected.squeeze(0).max(dim=-1, keepdim=False)[1]
# 增量更新(我们希望重复单词预测结果是一样的)
# 我们在预测是会选择性忽略重复的预测的词,只摘取最新预测的单词拼接到输入序列中
next_word = prob.data[-1] # 拿出当前预测的单词(数字)。我们用x'_t对应的输出z_t去预测下一个单词的概率,不用z_1,z_2..z_{t-1}
next_symbol = next_word
if next_symbol == tgt_vocab["E"]:
terminal = True
# print(next_word)
greedy_dec_predict = dec_input[:, 1:]
return greedy_dec_predict
# 测试集
sentences = [
# enc_input dec_input dec_output
['我 有 零 个 女 朋 友', '', '']
]
enc_inputs, dec_inputs, dec_outputs = make_data(sentences)
test_loader = Data.DataLoader(MyDataSet(enc_inputs, dec_inputs, dec_outputs), 2, True)
enc_inputs, _, _ = next(iter(test_loader))
print()
print("="*30)
print("利用训练好的Transformer模型将中文句子'我 有 零 个 女 朋 友' 翻译成英文句子: ")
for i in range(len(enc_inputs)):
greedy_dec_predict = greedy_decoder(model, enc_inputs[i].view(1, -1).to(device), start_symbol=tgt_vocab["S"])
print(enc_inputs[i], '->', greedy_dec_predict.squeeze())
print([src_idx2word[t.item()] for t in enc_inputs[i]], '->',
[idx2word[n.item()] for n in greedy_dec_predict.squeeze()])
参考:
https://ugirc.blog.csdn.net/article/details/120394042
https://zhuanlan.zhihu.com/p/338817680