😀大家好，我是白晨，一个不是很能熬夜，但是也想日更的人✈。如果喜欢这篇文章，点个赞👍，关注一下👀白晨吧！你的支持就是我最大的动力！💪💪💪

📗前言

---

大家好，我是白晨。本次为大家带来的常用数据结构的模拟实现，主要用于在算法比赛中快速实现一种常用模拟实现。那为什么不用STL呢？首先，STL为了保证其接口的通用性以及要严格符合一个数据结构的定义，在使用时可能不是非常方便；其次，模拟实现的数据结构在运行速度方面是要快于STL的容器的。

本篇文章将详细介绍单链表、双链表、栈、队列以及堆这五种常见数据结构的模拟实现，由于本次是面向新人的教程，白晨使用大量图片、动图和语言描述详细拆解一个模拟数据结构的实现。如果以前没有接触过这几类数据结构的同学可以先阅读每个标题下的文章。话不多说，我们开始吧。

---

📙常用数据结构（一）

---

🍉单链表

---

如果对于单链表还不是特别熟悉的同学可以先看白晨这篇文章——【数据结构】链表全解析。

• 逻辑结构

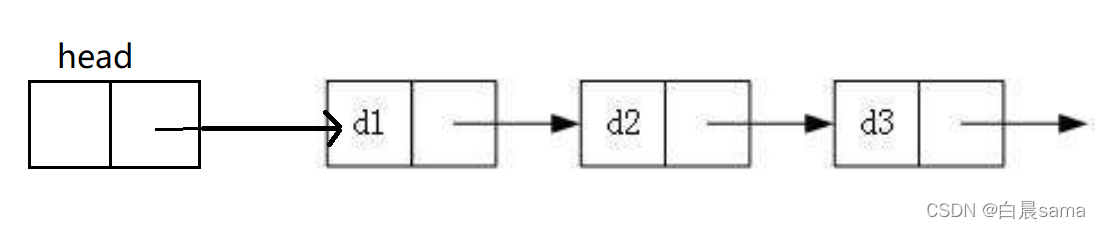
• 物理结构

本篇文章全部都是模拟实现。所以，这次我们选择用数组模拟单链表。

• 具体实现

1. 初始化

v数组存放结点值，ne存放下一个结点的下标，idx为当前可使用结点的下标。头节点默认为0。

const int N = 100010;

int v[N], ne[N]; // v数组存放结点值，ne存放下一个结点的下标
int idx; // 头节点默认为0，idx为当前可使用结点的下标

// 初始化
void init()
{
    idx = 1;
}

2. 在下标为k的结点后面插入

在下标为k的结点后面插入值为x的结点，只需要将新结点的值存入v数组中，然后将新结点的指针ne指向原来k结点的下一个结点，再将k结点的指针ne指向新结点即可。

如上图，每插入一个数据，v[idx]中填入一个数据，ne[idx]指向k（插入方式为头插），idx向后移动一次

void add(int k, int x)
{
    v[idx] = x;
    ne[idx] = ne[k]; // 头插
    ne[k] = idx++;
}

3. 删除下标为k结点后面的结点

删除下标为k结点后面的结点，只需要将k结点的指针ne指向下下个节点即可。

下标为2的结点本来指向下标为1的结点，删除2结点后面的结点也就是直接让ne[2]指向 ne[ne[2]] <==> ne[1] <==> 0。

void remove(int k)
{
    ne[k] = ne[ne[k]];
}

---

🍋双链表

---

如果对于双链表还不是特别熟悉的同学可以先看白晨这篇文章——【数据结构】链表全解析。

• 逻辑结构

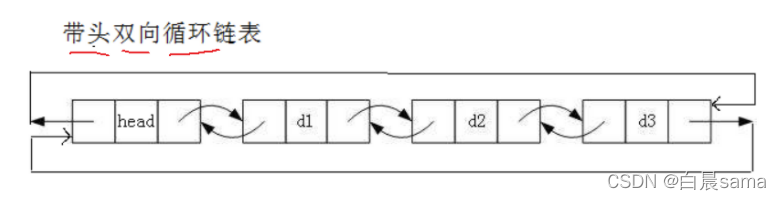
• 物理结构

同样数组模拟单链表。

• 具体实现

双链表使用没有单链表使用的多，但是双链表是基于单链表实现的，是个更深理解单链表实现的好例子。

1. 初始化

v数组存放结点值，l存放左边结点的下标，r存放右边结点的下标，head为左端点，tail为右端点，idx为当前可使用结点的下标。相当将双链表拆成了两个单链表，l从右指向左，r从左指向右。

const int N = 100010;

int v[N], l[N], r[N];
int head = 0, tail = 1, idx;

void init()
{
    l[0] = 1; // 0为左结点
    r[0] = 1;
    l[1] = 0; // 1为右结点
    r[1] = 0;
    idx = 2; // 从2开始插入数据
}

2. 在下标为k的数的右边插入

在下标为k的数的右边插入值为x的数，只需要将新数的值存入v数组中，然后将新数的左指针l指向k，右指针r指向k的右边结点r[k]。接着将k的右指针r[k]指向新数，新数的右边结点r[idx]的左指针l[r[idx]]指向新数即可。

void insert(int k, int x)
{
    v[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    r[k] = idx;
    l[r[idx]] = idx;
    idx++;
}

3. 删除下标为k的元素

删除下标为k的元素时，只需要将k的左边结点l[k]的右指针r[l[k]]指向k的右边结点r[k]，将k的右边结点r[k]的左指针l[r[k]]指向k的左边结点l[k]即可。

void erase(int k)
{
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

---

🥭栈

---

如果对于栈还不是特别熟悉的同学可以先看白晨这篇文章——【数据结构】栈结构全解析。

• 逻辑结构

• 物理结构

数组模拟栈。

• 具体实现

1. 初始化

定义了一个数组st和一个变量back，st用于存储栈中的元素，back表示栈顶元素的下标。

init函数用于初始化栈，将back设为-1表示栈为空。

const int N = 100010;

int st[N], back;

void init()
{
    back = -1;
}

2. 压栈

将元素x压入栈中，back加1表示栈顶指针向上移动一位，将x存入st[back]中。

void push(int x)
{
    st[++back] = x;
}

3. 出栈

弹出栈顶元素，back减1表示栈顶指针向下移动一位。

void pop()
{
    --back;
}

4. 取栈顶元素

返回栈顶元素，即st[back]。

int top()
{
    return st[back];
}

5. 判断栈是否为空

判断栈是否为空，即back是否小于0

bool empty()
{
    return back < 0;
}

• 练习题目

• 题目链接：表达式求值

• 参考解法：这里只给出使用STL中栈的解法，模拟栈解法大家可以自行实现，维护两个模拟栈即可，思路与STL栈没有任何区别。

#include <iostream>
#include <stack>
#include <unordered_map>
#include <cstdlib>
#include <string>

using namespace std;

stack<int> num;
stack<char> op;
unordered_map<char, int> dict{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; // 按照操作符优先级设置权值

void eval()
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();
    int x;
    
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;
    
    num.push(x);
}

int main()
{
    string str;
    cin >> str;
    
    for (int i = 0; i < str.size(); ++i)
    {
        char e = str[i];
        if (isdigit(e))
        {
            int j = i, x = 0;
            while (isdigit(str[j])) x = x * 10 + str[j++] - '0';
            num.push(x);
            i = j - 1;
        }
        else if (e == '(') op.push(e);
        else if (e == ')')
        {
            // 将括号中的数据运算完
            while (op.top() != '(') eval();
            op.pop();
        }
        else
        {
            // 如果当前操作符优先级 小于等于 前面操作符，就要算出前面操作符所操作的值
            while (op.size() && op.top() != '(' && dict[e] <= dict[op.top()]) eval();
            op.push(e);
        }
    }
    
    // 上面过程进行完，表达式中没有括号 并且 操作符的优先级是升序排列，此时将数据按出栈顺序计算即可
    while (op.size()) eval();
    
    cout << num.top() << endl;
    return 0;
}

---

🍊队列

---

如果对于队列还不是特别熟悉的同学可以先看白晨这篇文章——【数据结构】栈与队列全解析。

• 物理结构

数组模拟队列。

• 具体实现

1. 初始化

q为数组队列，front为队头下标，tail为队尾下标。

初始化队列，将队头指针front赋值为0，将队尾指针tail赋值为-1。

const int N = 100010;

int q[N], front, tail;

void init()
{
    front = 0, tail = -1;
}

2. 入队

将元素x插入到队列的末尾。由于数组下标从0开始，因此需要先将tail加1，然后再将x插入到q[tail]中。

void push(int x)
{
    q[++tail] = x;
}

3. 出队

弹出队首元素。由于数组下标从0开始，因此只需要将front加1即可。

void pop()
{
    ++front;
}

4. 取队头元素

返回队首元素。由于数组下标从0开始，因此只需要返回q[front]即可。

int top()
{
    return q[front];
}

5. 判断队列是否为空

当 front > tail下标时，这个队列为空

bool empty()
{
    return front > tail;
}

---

🍎堆

---

如果对于堆还不是特别熟悉的同学可以先看白晨这篇文章——【数据结构】堆的全解析。

• 逻辑结构

小根堆

大根堆

• 物理结构

数组模拟堆。

• 具体实现

由于大小根堆的实现思路大致相同，这里具体讲解小根堆的实现思路，大根堆只需要将结点元素比较时的比较符号取反即可。

1. 初始化

这个堆是用数组来实现的，下标从1开始。数组h存储了堆中的元素，Size表示堆中元素的个数。

const int N = 100010;

int h[N], Size; 

2. 将堆中下标为x的数向下调整

1. 保证要调整结点x的左右子树都是小堆。
2. 比较N与孩子结点的大小关系。如果x小于等于两个孩子结点，调整结束；不然就让x与较小的孩子交换。
3. 重复2过程，直到x调整结束或者被调整到叶子结点。

首先将cur赋值为x，然后判断2 * x和2 * x + 1是否小于等于Size，如果是，则将cur赋值为其中较小的那个。如果cur不等于x，则交换h[x]和h[cur]，然后递归调用down(cur)。

void down(int x)
{
    int cur = x;
    // 大根堆将 h[cur] > h[2 * x] 和 h[cur] > h[2 * x + 1] 改为 h[cur] < h[2 * x] 和 h[cur] < h[2 * x + 1]
    if (2 * x <= Size && h[cur] > h[2 * x]) cur = 2 * x;
    if (2 * x + 1 <= Size && h[cur] > h[2 * x + 1]) cur = 2 * x + 1;

    if (cur != x)
    {
        swap(h[x], h[cur]);
        down(cur);
    }
}

3. 将堆中下标为x的数向上调整

1. 保证要调整结点x的祖先是满足小堆性质的。
2. 比较x与父结点的大小关系。如果x大于父结点，调整结束；不然就让x与父节点交换。
3. 重复2过程，直到x调整结束或者被调整到根结点。

首先将cur赋值为x，然后判断cur / 2是否大于0且h[cur / 2]是否大于h[cur]，如果是，则交换h[cur / 2]和h[cur]，然后将cur除以2。重复这个过程直到cur / 2等于0或者h[cur / 2]不大于h[cur]。

void up(int x)
{
    int cur = x;
    // 大根堆将 h[cur / 2] > h[cur] 改为 h[cur / 2] < h[cur]
    while (cur / 2 && h[cur / 2] > h[cur])
    {
        swap(h[cur / 2], h[cur]);
        cur /= 2;
    }
}

4. 向下建堆

从第一个非叶子节点Size/2开始向下调整，直到调整到根节点。时间复杂度约为O(N)。

如果有[31, 30, 29, …, 1]这一组数据建堆，建堆过程如下：

void build()
{
	for (int i = Size / 2; i; --i) down(i);
}

5. 将x插入堆

Size++，再将x赋予h[Size]，再向上调整h[Size]。时间复杂度为O(logN)

在[10, 9, 8, …, 1]所建成的堆中，插入一个0：

void insert(int x)
{
    Size++;
    h[Size] = x;
    up(Size);
}

6. 删除堆顶元素

• 我们可以将栈顶元素与栈底元素交换，然后删除数组最后一个数据，这时候栈顶元素已经被删除了。
• 现在根结点左右子树都是小堆，所以我们可以使用向下调整，调整根结点的位置，重新构建成堆。

首先交换h[1]和h[Size]，然后将Size减1，最后调用down(1)。

删除堆顶元素：

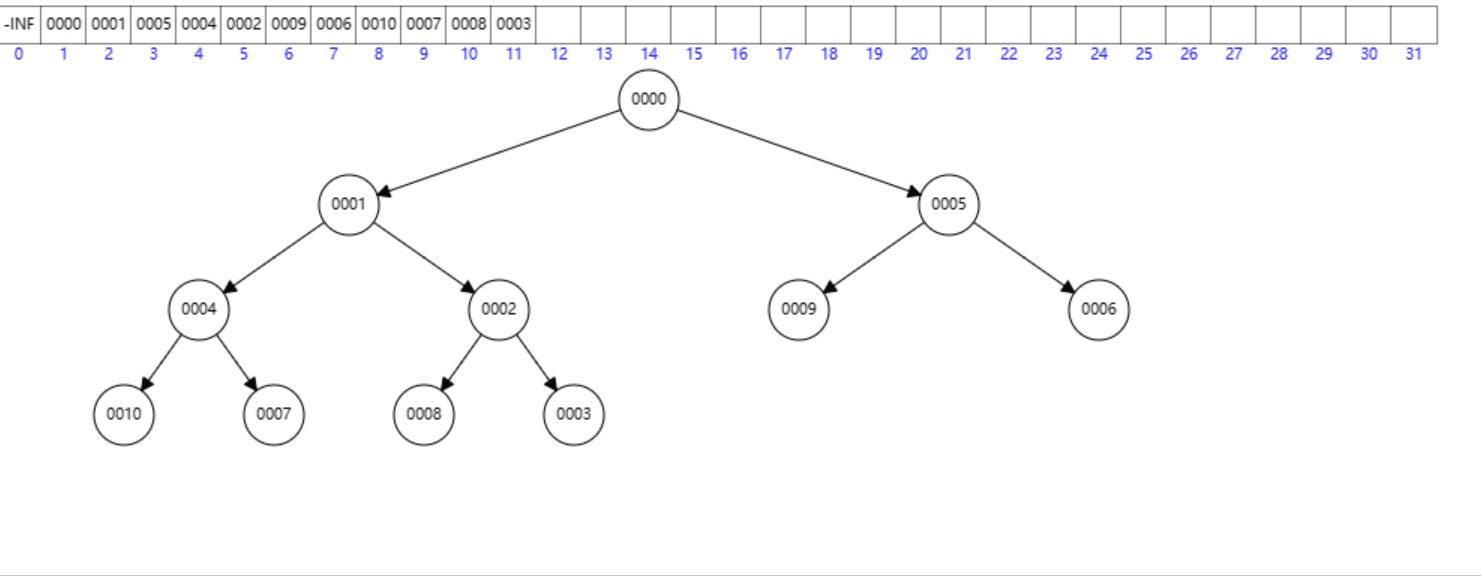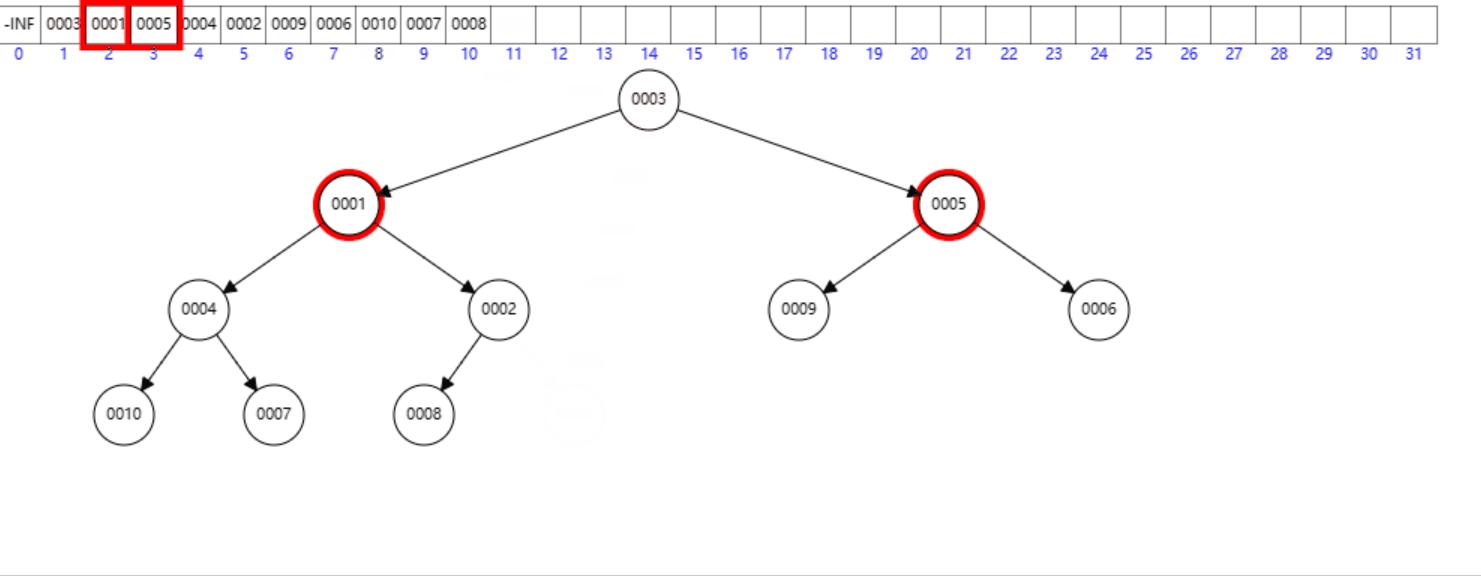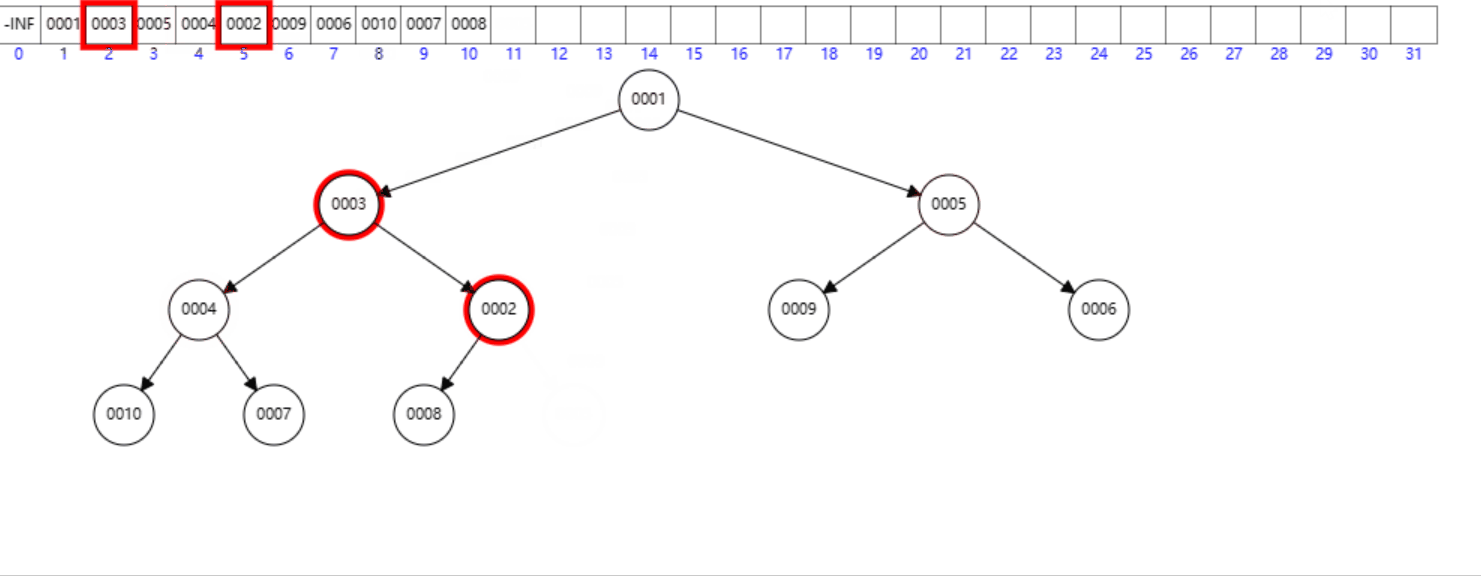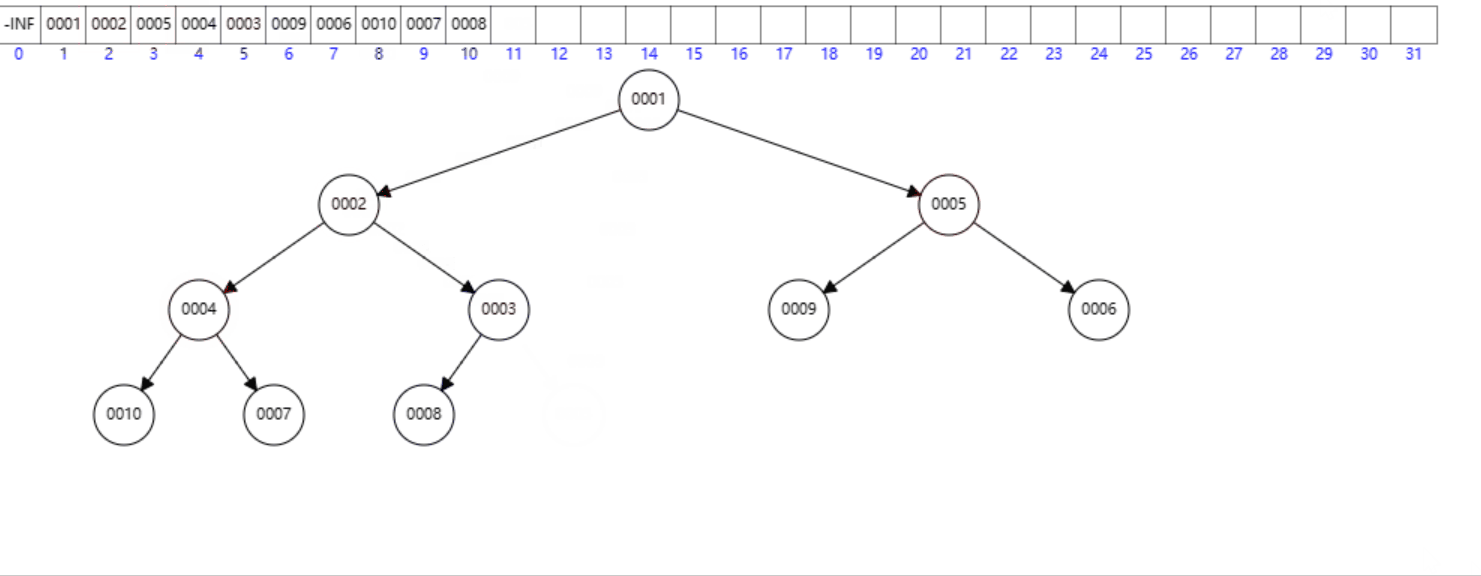
void erase()
{
    swap(h[1], h[Size]);
    Size--;
    down(1);
}

• 练习题目

🍬原题链接：堆排序

🪅算法思想：

• 先建堆，再一个个删除，按照堆的性质，就能得到一串排好序的序列。

🪆代码实现：

#include <iostream>

using namespace std;

const int N = 100010;

int h[N], Size; // 下标从1开始，小根堆

// 将堆中下标为x的数向下调整
void down(int x)
{
    int cur = x;
    if (2 * x <= Size && h[cur] > h[2 * x]) cur = 2 * x;
    if (2 * x + 1 <= Size && h[cur] > h[2 * x + 1]) cur = 2 * x + 1;

    if (cur != x)
    {
        swap(h[x], h[cur]);
        down(cur);
    }
}

// 将堆中下标为x的数向上调整
void up(int x)
{
    int cur = x;
    while (cur / 2 && h[cur / 2] > h[cur])
    {
        swap(h[cur / 2], h[cur]);
        cur /= 2;
    }
}

void erase()
{
    swap(h[1], h[Size]);
    Size--;
    down(1);
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    // 向下建堆，时间复杂度为O(n)
    // n / 2 为最后一个有叶结点的结点
    for (int i = 1; i <= n; ++i) scanf("%d", &h[i]);
    Size = n;
    for (int i = n / 2; i; --i) down(i);
  

    while (m--)
    {
        printf("%d ", h[1]);
        erase();
    }
    return 0;
}

---

📘后记

---

本篇文章的数据结构非常重要，不仅是常用数据结构（二）的引子，也是以后图论等算法的基础，最好能将其拿下。

如果讲解的有不对之处还请指正，我会尽快修改，多谢大家的包容。

如果大家喜欢这个系列，还请大家多多支持啦😋！

如果这篇文章有帮到你，还请给我一个大拇指 👍和小星星 ⭐️支持一下白晨吧！喜欢白晨【算法】系列的话，不如关注👀白晨，以便看到最新更新哟！！！

我是不太能熬夜的白晨，我们下篇文章见。

---