主成分分析的统计学视角
文章目录
- 主成分分析的统计学视角
- PCA 的统计学视角
- 1. 寻找第一个主成分
- 2. 获取第二个主成分
- 3. 非零均值随机变量的主元
- 4. 零均值随机变量的样本主元
- 5. PCA 降维案例
主成分分析是将高维空间中的数据集拟合成一个低维子空间的方法,到目前为止它已成功应用于数学建模、数据压缩、数据可视化等领域。
主成分分析是将高维空间的数据集 { x i ∈ R D ∣ i = 1 , 2 , ⋯ , n } \{\boldsymbol{x}_i\in\mathbb{R}^D\vert i=1,2,\cdots,n\} {xi∈RD∣i=1,2,⋯,n} 拟合到一个低维放射子空间 S S S 中,且其维数 d ≪ D d\ll D d≪D。该问题可视为统计问题或者代数几何问题。
PCA 的统计学视角
多维随机变量
x
∈
R
D
\boldsymbol{x}\in \mathbb{R}^D
x∈RD 满足
E
[
x
]
=
0
\mathbb{E}[\boldsymbol{x}]=\boldsymbol{0}
E[x]=0,可寻找
d
(
≪
D
)
d\;\;(\ll D)
d(≪D) 个主元
y
i
(
i
=
1
,
2
,
⋯
,
d
)
y_i\;\;(i=1,2,\cdots,d)
yi(i=1,2,⋯,d),使
y
=
[
y
1
,
y
2
,
⋯
,
y
d
]
⊤
\boldsymbol{y}=[y_1,y_2,\cdots,y_d]^\top
y=[y1,y2,⋯,yd]⊤ 可表示为
x
\boldsymbol{x}
x 的
d
d
d 个不线性相关的成分
y
=
[
y
1
y
2
⋮
y
d
]
=
[
u
1
⊤
x
u
2
⊤
x
⋮
u
d
⊤
x
]
=
[
u
1
⊤
u
2
⊤
⋮
u
d
⊤
]
x
=
U
⊤
x
\boldsymbol{y}=\begin{bmatrix} y_1\\ y_2 \\ \vdots \\ y_d \end{bmatrix} =\begin{bmatrix} \boldsymbol{u}_1^\top\boldsymbol{x}\\ \boldsymbol{u}_2^\top\boldsymbol{x}\\ \vdots \\ \boldsymbol{u}_d^\top\boldsymbol{x}\\ \end{bmatrix} =\begin{bmatrix} \boldsymbol{u}_1^\top\\ \boldsymbol{u}_2^\top\\ \vdots \\ \boldsymbol{u}_d^\top\\ \end{bmatrix}\boldsymbol{x} =U^\top\boldsymbol{x}
y=
y1y2⋮yd
=
u1⊤xu2⊤x⋮ud⊤x
=
u1⊤u2⊤⋮ud⊤
x=U⊤x
或
y
i
=
u
i
⊤
x
,
i
=
1
,
2
,
⋯
,
d
y_i=\boldsymbol{u}_i^\top\boldsymbol{x},\qquad i=1,2,\cdots,d
yi=ui⊤x,i=1,2,⋯,d
满足
u
i
⊤
u
i
=
1
,
u
i
⊤
u
j
=
0
\boldsymbol{u}_i^\top\boldsymbol{u}_i=1,\;\;\boldsymbol{u}_i^\top\boldsymbol{u}_j=0
ui⊤ui=1,ui⊤uj=0 且
Var
[
y
1
]
≥
Var
[
y
2
]
≥
⋯
≥
Var
[
y
d
]
\text{Var}[y_1]\geq \text{Var}[y_2]\geq\cdots\geq\text{Var}[y_d]
Var[y1]≥Var[y2]≥⋯≥Var[yd],其中,
y
1
,
y
2
,
⋯
,
y
d
y_1,y_2,\cdots,y_d
y1,y2,⋯,yd 分别称为
x
\boldsymbol{x}
x 的第1、第2、
⋯
\cdots
⋯、第
d
d
d 个主成分.
1. 寻找第一个主成分
以第一主成分为例,我们试图寻找向量
u
1
∗
\boldsymbol{u}_1^*
u1∗ 使得
max
u
1
∗
∈
R
D
Var
[
u
1
⊤
x
]
s
.
t
.
u
1
⊤
u
1
=
1
\begin{align*} \max_{\boldsymbol{u}_1^*\in\mathbb{R}^D} \quad \text{Var}[\boldsymbol{u}_1^{\top}\boldsymbol{x}] \\ s.t. \quad\boldsymbol{u}_1^{\top}\boldsymbol{u}_1=1 \end{align*}
u1∗∈RDmaxVar[u1⊤x]s.t.u1⊤u1=1
定理:(随机变量的主成分)
对于随机变量
x
∈
R
D
\boldsymbol{x}\in\mathbb{R}^D
x∈RD 且满足
E
[
x
]
=
0
\mathbb{E}[\boldsymbol{x}]=\boldsymbol{0}
E[x]=0,协方差矩阵为
Σ
x
=
E
[
x
x
⊤
]
\Sigma_{\boldsymbol{x}}=\mathbb{E}[\boldsymbol{x}\boldsymbol{x}^\top]
Σx=E[xx⊤],假设
rank
(
Σ
x
)
≥
d
\text{rank}(\Sigma_{\boldsymbol{x}})\geq d
rank(Σx)≥d,则多维随机变量
x
\boldsymbol{x}
x 的第
i
i
i 个主成分
y
i
y_i
yi 可表示为
y
i
=
u
i
⊤
x
y_i=\boldsymbol{u}_i^\top\boldsymbol{x}
yi=ui⊤x
其中,
{
u
i
}
i
=
1
d
\{\boldsymbol{u}_i\}_{i=1}^d
{ui}i=1d 是协方差矩阵
Σ
x
\Sigma_{\boldsymbol{x}}
Σx 的第
i
i
i 个最大特征值对应的特征向量(相互正交),且
λ
i
=
Var
[
y
i
]
\boldsymbol\lambda_i=\text{Var}[\boldsymbol y_i]
λi=Var[yi].
证明: 为简单起见,假定
Σ
x
\Sigma_{\boldsymbol{x}}
Σx 无重复特征值。由
Σ
x
u
j
=
λ
j
u
j
\Sigma_{\boldsymbol{x}}\boldsymbol{u}_j=\lambda_j\boldsymbol{u}_j
Σxuj=λjuj 或
u
j
⊤
Σ
x
=
λ
j
u
j
⊤
\boldsymbol{u}_j^\top\Sigma_{\boldsymbol{x}}=\lambda_j\boldsymbol{u}_j^\top
uj⊤Σx=λjuj⊤ 知
u
i
⊤
Σ
x
u
j
⏟
=
λ
j
u
i
⊤
u
j
u
i
⊤
Σ
x
⏟
u
j
=
λ
i
u
i
⊤
u
j
\boldsymbol{u}_i^\top\underbrace{\Sigma_{\boldsymbol{x}}\boldsymbol{u}_j}=\lambda_j\boldsymbol{u}_i^\top\boldsymbol{u}_j\\ \underbrace{\boldsymbol{u}_i^\top\Sigma_{\boldsymbol{x}}}\boldsymbol{u}_j=\lambda_i\boldsymbol{u}_i^\top\boldsymbol{u}_j
ui⊤
Σxuj=λjui⊤uj
ui⊤Σxuj=λiui⊤uj
即
(
λ
i
−
λ
j
)
u
i
⊤
u
j
=
0
(\boldsymbol\lambda_i-\boldsymbol\lambda_j)\boldsymbol{u}_i^\top\boldsymbol{u}_j=0
(λi−λj)ui⊤uj=0,又由于
λ
i
≠
λ
j
\boldsymbol\lambda_i\ne\boldsymbol\lambda_j
λi=λj,可知
u
i
⊤
u
j
=
0
\boldsymbol{u}_i^\top\boldsymbol{u}_j=0
ui⊤uj=0
由于
Var
[
y
i
]
=
Var
[
u
i
⊤
x
]
=
E
[
(
u
i
⊤
x
)
2
]
=
E
[
u
i
⊤
x
x
⊤
u
i
]
=
u
i
⊤
E
[
x
x
⊤
]
u
i
=
u
i
Σ
x
u
i
\begin{aligned} \operatorname{Var}\left[\boldsymbol y_{i}\right] &=\operatorname{Var}\left[\boldsymbol{u_{i}^{\top}} \boldsymbol x\right]=E\left[\left(u_{i}^{\top} x\right)^{2}\right] \\ &=E\left[\boldsymbol {u_{i}^{\top}} \boldsymbol x \boldsymbol{x^{\top}} \boldsymbol u_{i}\right]=\boldsymbol{u_{i}^{\top}} E\left[\boldsymbol x \boldsymbol{x^{\top}}\right] u_{i}=\boldsymbol u_{i} \Sigma_{x} \boldsymbol u_{i} \end{aligned}
Var[yi]=Var[ui⊤x]=E[(ui⊤x)2]=E[ui⊤xx⊤ui]=ui⊤E[xx⊤]ui=uiΣxui
则优化问题
max
Var
[
y
1
]
\max \operatorname{Var}\left[\boldsymbol y_{1}\right]
maxVar[y1]可建模为
{
max
u
1
∈
R
D
u
1
⊤
Σ
x
u
1
s.t.
u
1
⊤
u
1
=
1
\left\{\begin{array}{l} \max _{\boldsymbol{u}_1\in\mathbb{R}^D} \boldsymbol u_1^{\top} \Sigma_x \boldsymbol u_1 \\ \text { s.t. } \boldsymbol{u_1^{\top}} \boldsymbol u_1=1 \end{array}\right.
{maxu1∈RDu1⊤Σxu1 s.t. u1⊤u1=1
构造拉格朗日函数,将约束优化化成无约束优化
L
(
u
1
)
=
u
1
⊤
Σ
x
u
1
+
λ
(
1
−
u
1
⊤
u
1
)
\mathcal{L}\left( \boldsymbol{u}_{1}\right)= \boldsymbol{u}_{1}^{\top} \ {\Sigma}_{\boldsymbol{x}} \boldsymbol{u}_{1}+\boldsymbol{\lambda}\left(1-\boldsymbol{{u}_{1}^{\top}} \boldsymbol{u}_{1}\right)
L(u1)=u1⊤ Σxu1+λ(1−u1⊤u1)
偏导数值为零
∂
L
(
u
1
)
∂
u
1
=
2
Σ
x
u
1
−
2
λ
u
1
=
2
(
Σ
x
u
1
−
λ
u
1
)
=
0
\frac{\partial \mathcal{L}\left(\boldsymbol{u}_{1}\right)}{\partial \boldsymbol{u}_{1}}=2 \ {\Sigma}_{x} \boldsymbol{u}_{1}-2 \boldsymbol{\lambda} \boldsymbol {u}_{1}=2\left(\ {\Sigma}_{x} \boldsymbol {u}_{1}-\boldsymbol\lambda \boldsymbol {u}_{1}\right)=0
∂u1∂L(u1)=2 Σxu1−2λu1=2( Σxu1−λu1)=0
即
Σ
x
u
1
=
λ
u
1
{\Sigma}_{x} \boldsymbol {u}_{1}=\boldsymbol \lambda \boldsymbol {u}_{1}
Σxu1=λu1
可知
u
1
{u}_{1}
u1是协方差矩阵
∑
x
{\sum}_{x}
∑x的特征值
λ
\boldsymbol\lambda
λ对应的特征向量,最优值
u
1
⊤
∑
x
u
1
=
λ
u
1
u
1
⊤
=
λ
1
>
0
\boldsymbol{ {u}_{1}^{\top}} {\sum}_{x} \boldsymbol u_{1}=\boldsymbol\lambda \boldsymbol u_{1} \boldsymbol{u_{1}^{\top}}=\boldsymbol\lambda_{1}>0
u1⊤∑xu1=λu1u1⊤=λ1>0。
2. 获取第二个主成分
第二个最优解
u
2
\boldsymbol{u}_2
u2 需要满足随机变量
y
1
=
u
1
⊤
x
y_{1}=\boldsymbol{u_{1}^{\top}} \boldsymbol x
y1=u1⊤x 与随机变量
y
2
=
u
2
⊤
x
y_{2}=\boldsymbol{u_{2}^{\top}} \boldsymbol x
y2=u2⊤x 不相关,即
u
1
⊥
u
2
\boldsymbol {u}_{1} \perp \boldsymbol {u}_{2}
u1⊥u2. 由于
E
[
x
]
=
0
\mathbb{E}[\boldsymbol x]=\boldsymbol 0
E[x]=0,则
E
[
y
i
]
=
E
[
u
i
⊤
x
]
=
0
\mathbb{E}[y_i]=\mathbb{E}[\boldsymbol u^\top_i\boldsymbol x]=0
E[yi]=E[ui⊤x]=0. 两个随机变量的协方差可表示为
Cov
(
y
1
,
y
2
)
=
Cov
(
u
1
⊤
x
,
u
2
⊤
x
)
=
E
[
(
u
1
⊤
x
)
(
u
2
⊤
x
)
⊤
]
=
E
[
u
1
⊤
x
x
⊤
u
2
]
=
u
1
⊤
Σ
x
u
2
=
λ
1
u
1
⊤
u
2
=
0
\begin{array}{l} \operatorname{Cov}\left(y_{1}, y_{2}\right)=\operatorname{Cov}\left(\boldsymbol {{u}_{1}^{\top}} \boldsymbol x, \boldsymbol {u_{2}^{\top}}\boldsymbol x\right)=E\left[\left(\boldsymbol{u_{1}^{\top}} \boldsymbol x\right)\left(\boldsymbol{u_{2}^{\top}} \boldsymbol x\right)^{\top}\right] \\ =E\left[\boldsymbol {{u}_{1}^{\top}} \boldsymbol x \boldsymbol{x^{\top}} \boldsymbol {u}_{2}\right]=\boldsymbol {{u}_{1}^{\top}} \Sigma_{\boldsymbol x} \boldsymbol {u}_{2}=\boldsymbol\lambda_{1} \boldsymbol{u_{1}^{\top}} \boldsymbol u_{2}=0 \end{array}
Cov(y1,y2)=Cov(u1⊤x,u2⊤x)=E[(u1⊤x)(u2⊤x)⊤]=E[u1⊤xx⊤u2]=u1⊤Σxu2=λ1u1⊤u2=0
可知
u
1
⊤
u
2
=
0
\boldsymbol {u_1^{\top}} \boldsymbol u_2=0
u1⊤u2=0,
则优化模型为
max
u
2
∈
R
D
Var
[
y
2
]
=
u
2
⊤
Σ
x
u
2
s.t.
u
2
⊤
u
2
=
1
u
1
⊤
u
2
=
0
\begin{array}{l} \max_{\boldsymbol{u}_2 \in\mathbb R^{D}} \operatorname{Var}\left[y_{2}\right]=\boldsymbol {u}_{2}^{\top} \Sigma_{x} \boldsymbol u_{2}\\ \text { s.t. } \;\;\boldsymbol {{u}_{2}^{\top}} \boldsymbol {u}_{2}=1 \\ \qquad\;\;\boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{2}=0 \end{array}
maxu2∈RDVar[y2]=u2⊤Σxu2 s.t. u2⊤u2=1u1⊤u2=0
构造拉格朗日函数
L
(
u
2
,
λ
2
,
γ
)
=
u
2
⊤
Σ
x
u
2
+
λ
2
(
1
−
u
2
⊤
u
2
)
+
γ
u
1
⊤
u
2
\mathcal{L}\left(\boldsymbol {u}_{2}, \boldsymbol\lambda_2,\boldsymbol\gamma \right)=\boldsymbol {{u}_{2}^{\top}} {\Sigma}_x \boldsymbol {u}_{2}+\boldsymbol\lambda_{2}\left(1-\boldsymbol {{u}_{2}^{\top}} \boldsymbol {u}_{2}\right)+\boldsymbol\gamma \boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{2}
L(u2,λ2,γ)=u2⊤Σxu2+λ2(1−u2⊤u2)+γu1⊤u2
置偏导数为0,得
∂
L
(
u
2
,
λ
2
,
γ
)
∂
u
2
=
2
Σ
x
u
2
−
2
λ
2
u
2
+
γ
u
1
=
0
(1)
\frac{\partial \mathcal{L}\left(\boldsymbol u_{2}, \boldsymbol\lambda_{2}, \boldsymbol\gamma\right)}{\partial \boldsymbol {u}_{2}}=2 {\Sigma}_{x} \boldsymbol {u}_{2}-2 \boldsymbol\lambda_{2} \boldsymbol {u}_{2}+\boldsymbol\gamma \boldsymbol {u}_{1}=\ {0} \tag{1}
∂u2∂L(u2,λ2,γ)=2Σxu2−2λ2u2+γu1= 0(1)
∂ L ( u 2 , λ 2 , γ ) ∂ λ 2 = 1 − u 2 ⊤ u 2 = 0 \frac{\partial \mathcal{L}\left(\boldsymbol {u}_{2}, \boldsymbol\lambda_{2}, \boldsymbol\gamma\right)}{\partial \boldsymbol\lambda_{2}}=1-\boldsymbol {{u}_{2}^{\top}} \boldsymbol{u}_{2}=0 ∂λ2∂L(u2,λ2,γ)=1−u2⊤u2=0
∂ L ( u 2 , λ 2 , γ ) ∂ γ = u 2 ⊤ u 2 = 0 \frac{\partial \mathcal{L}\left(\boldsymbol {u}_{2}, \boldsymbol\lambda_{2}, \boldsymbol\gamma\right)}{\partial \boldsymbol\gamma}=\boldsymbol {{u}_{2}^{\top}} \boldsymbol{u}_{2}=0 ∂γ∂L(u2,λ2,γ)=u2⊤u2=0
(1) 式两边同时左乘
u
1
⊤
\boldsymbol{{u}_{1}^{\top}}
u1⊤得
2
u
1
⊤
Σ
x
u
2
−
2
λ
2
u
1
⊤
u
2
+
γ
u
1
⊤
u
1
=
0
2
λ
1
u
1
⊤
u
2
−
2
λ
2
u
1
⊤
u
2
+
γ
=
0
\begin{array}{l} 2 \boldsymbol {{u}_{1}^{\top}} \Sigma_{x} \boldsymbol {u}_{2}-2 \boldsymbol\lambda_{2} \boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{2}+\boldsymbol\gamma \boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{1}=0 \\ 2 \boldsymbol\lambda_{1} \boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{2}-2 \boldsymbol\lambda_{2} \boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{2}+\boldsymbol\gamma=0 \end{array}
2u1⊤Σxu2−2λ2u1⊤u2+γu1⊤u1=02λ1u1⊤u2−2λ2u1⊤u2+γ=0
即
γ
=
2
(
λ
2
−
λ
1
)
u
1
⊤
u
2
=
0
\boldsymbol\gamma=2\left(\boldsymbol\lambda_{2}-\boldsymbol\lambda_{1}\right) \boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{2}=0
γ=2(λ2−λ1)u1⊤u2=0
则 (1) 式可简化为
Σ
x
u
2
=
λ
2
u
2
{\Sigma}_ {\boldsymbol x} \boldsymbol {u}_{2}=\boldsymbol\lambda_{2} \boldsymbol {u}_{2}
Σxu2=λ2u2
说明最优解
u
2
\boldsymbol{u}_{2}
u2 为协方差矩阵
Σ
x
\Sigma_{\boldsymbol x}
Σx 的第二大特征值
λ
2
\boldsymbol\lambda_2
λ2对应的特征向量,此时的极值
max
u
2
⊤
Σ
x
u
2
=
λ
2
u
2
⊤
u
2
=
λ
2
\max \boldsymbol {{u}_{2}^{\top}} {\Sigma}_{x} \boldsymbol u_2=\boldsymbol\lambda_{2} \boldsymbol {{u}_{2}^{\top}} \boldsymbol {u}_{2}=\boldsymbol\lambda_{2}
maxu2⊤Σxu2=λ2u2⊤u2=λ2
对于其余的主元
y
i
y_i
yi与
y
i
(
i
≠
j
)
y_i(i\not=j)
yi(i=j)需满足
y
i
=
u
i
⊤
x
y_{i}=\boldsymbol{u}_i^{\top}\boldsymbol x
yi=ui⊤x 与
y
j
=
u
j
⊤
x
y_{j}=\boldsymbol {u}_{j}^{\top}\boldsymbol x
yj=uj⊤x 不相关,即
Cov
(
y
i
,
y
j
)
=
E
[
u
i
⊤
x
x
⊤
u
j
]
=
u
i
⊤
Σ
x
u
j
=
0
\operatorname{Cov}\left( y_{i}, y_{j}\right)=E\left[\boldsymbol {{u}_{i}^{\top}} \boldsymbol {x} \boldsymbol{x^{\top}}\boldsymbol {u}_{j}\right]=\boldsymbol {{u}_{i}^{\top}} \ {\Sigma}_x \boldsymbol {u}_{j}=0
Cov(yi,yj)=E[ui⊤xx⊤uj]=ui⊤ Σxuj=0
假设
u
1
,
u
2
,
⋯
,
u
i
−
1
\boldsymbol {u}_{1}, \boldsymbol {u}_{2}, \cdots, \boldsymbol {u}_{i-1}
u1,u2,⋯,ui−1为协方差矩阵
Σ
x
{\Sigma}_x
Σx的最大
i
−
1
i-1
i−1个归一化的特征向量,而最优解
u
i
\boldsymbol {u}_i
ui定义为第
i
i
i个主元
y
i
\boldsymbol y_i
yi对应的向量(未必为特征向量)。由前过程可知
Σ
x
u
j
=
λ
j
u
j
j
=
1
,
2
,
⋯
,
i
−
1
\ {\Sigma}_x \boldsymbol {u}_{j}=\boldsymbol\lambda_{j} \boldsymbol {u}_{j}\qquad j=1,2, \cdots, i-1
Σxuj=λjujj=1,2,⋯,i−1
且满足
u
i
⊤
Σ
x
u
j
=
λ
j
u
i
⊤
u
j
=
0
j
=
1
,
2
,
⋯
,
i
−
1
,
λ
j
>
0
\boldsymbol {u_i^{\top}}\ {\Sigma}_{x} \boldsymbol u_j = \boldsymbol\lambda_j \boldsymbol {u_i^{\top}} \boldsymbol u_j = 0 \qquad j=1,2, \cdots, i-1,\qquad \lambda_j>0
ui⊤ Σxuj=λjui⊤uj=0j=1,2,⋯,i−1,λj>0
即
u
i
⊤
u
j
=
0
j
=
1
,
2
,
⋯
,
i
−
1
\boldsymbol{u_i^{\top}} \boldsymbol u_j=0 \qquad j=1,2, \cdots, i-1
ui⊤uj=0j=1,2,⋯,i−1
最优化模型为
{
max
V
a
r
[
y
i
]
=
u
i
⊤
Σ
x
u
i
s.t.
u
i
⊤
u
i
=
1
u
i
⊤
u
j
=
0
j
=
1
,
2
,
⋯
,
i
−
1
\left\{\begin{array}{l} \max Var[y_i] = \boldsymbol u_i^{\top} \Sigma_{\boldsymbol x} \boldsymbol u_i \\ \text { s.t. } \boldsymbol u_i^{\top} \boldsymbol u_i=1\\ \qquad \boldsymbol u_i^{\top} \boldsymbol u_j = 0 \qquad j = 1,2,\cdots,i-1 \end{array}\right.
⎩
⎨
⎧maxVar[yi]=ui⊤Σxui s.t. ui⊤ui=1ui⊤uj=0j=1,2,⋯,i−1
构造拉格朗日函数
L
(
u
i
,
λ
i
,
γ
j
)
=
u
i
⊤
Σ
x
u
i
+
λ
i
(
1
−
u
i
⊤
u
i
)
+
∑
j
=
1
i
−
1
γ
j
u
i
⊤
u
j
\mathcal{L}\left(\boldsymbol {u}_{i}, \boldsymbol\lambda_i,\boldsymbol\gamma_j \right)=\boldsymbol {{u}_{i}^{\top}} {\Sigma}_ x \boldsymbol {u}_{i}+\boldsymbol\lambda_{i}\left(1-\boldsymbol {{u}_{i}^{\top}} \boldsymbol {u}_{i}\right)+\sum_{j=1}^{i-1}\boldsymbol\gamma_j \boldsymbol {{u}_{i}^{\top}} \boldsymbol {u}_{j}
L(ui,λi,γj)=ui⊤Σxui+λi(1−ui⊤ui)+j=1∑i−1γjui⊤uj
置偏导数为0,得
∂
L
(
u
i
,
λ
i
,
γ
j
)
∂
u
i
=
2
Σ
x
u
i
−
2
λ
i
u
i
+
∑
j
=
1
i
−
1
γ
j
u
j
=
0
(2)
\frac{\partial \mathcal{L}\left(\boldsymbol u_{i}, \boldsymbol\lambda_{i}, \boldsymbol\gamma_j\right)}{\partial \boldsymbol {u}_{i}}=2 {\Sigma}_{x} \boldsymbol {u}_{i}-2 \boldsymbol\lambda_{i} \boldsymbol {u}_{i}+\sum_{j=1}^{i-1}\boldsymbol\gamma_j \boldsymbol {u}_{j}=\ {0}\tag{2}
∂ui∂L(ui,λi,γj)=2Σxui−2λiui+j=1∑i−1γjuj= 0(2)
∂ L ( u i , λ i , γ j ) ∂ λ i = 1 − u i ⊤ u i = 0 \frac{\partial \mathcal{L}\left(\boldsymbol u_{i}, \lambda_{i}, \boldsymbol\gamma_j\right)}{\partial \ {\lambda}_{i}}=1-\boldsymbol {u_i^{\top}} \boldsymbol u_i = {0} ∂ λi∂L(ui,λi,γj)=1−ui⊤ui=0
∂ L ( u i , λ i , γ j ) ∂ γ j = u i ⊤ u j = 0 j = 1 , 2 , ⋯ , i − 1 \frac{\partial \mathcal{L}\left(\boldsymbol u_{i}, \boldsymbol\lambda_{i}, \boldsymbol\gamma_j\right)}{\partial \ {\boldsymbol\gamma}_{j}}=\boldsymbol{u_i^{\top}} \boldsymbol u_j = 0 \qquad j = 1,2, \cdots ,i-1 ∂ γj∂L(ui,λi,γj)=ui⊤uj=0j=1,2,⋯,i−1
(2)式两边同时左乘
u
j
⊤
\boldsymbol{u_j^{\top}}
uj⊤,得
2
u
j
⊤
Σ
x
u
i
−
2
λ
i
u
j
⊤
u
i
+
∑
j
=
1
i
−
1
γ
j
u
j
⊤
u
j
=
0
2
λ
j
u
j
⊤
u
i
−
2
λ
j
u
j
⊤
u
i
+
∑
j
=
1
i
−
1
γ
j
=
0
\boldsymbol{2u_j^{\top}} \Sigma_ x \boldsymbol u_i-2\lambda_i \boldsymbol {u_j^{\top}} \boldsymbol u_i + \sum_{j=1}^{i-1} \boldsymbol\gamma_j \boldsymbol u_j^{\top} \boldsymbol u_j=0 \\ 2\lambda_j \boldsymbol u_j^{\top} \boldsymbol u_i - 2\lambda_j \boldsymbol{u_j^{\top}} \boldsymbol u_i + \sum_{j=1}^{i-1} \boldsymbol\gamma_j = 0
2uj⊤Σxui−2λiuj⊤ui+j=1∑i−1γjuj⊤uj=02λjuj⊤ui−2λjuj⊤ui+j=1∑i−1γj=0
即
∑
j
=
1
i
−
1
γ
j
=
2
(
λ
j
−
λ
i
)
u
j
⊤
u
i
=
0
\sum_{j=1}^{i-1} \boldsymbol\gamma_j = 2 \left(\lambda_j - \lambda_i \right) \boldsymbol {u_j^{\top}} \boldsymbol u_i = 0
j=1∑i−1γj=2(λj−λi)uj⊤ui=0
由拉格朗日乘子 γ j \boldsymbol\gamma_j γj非负,则 γ j = 0 j = 1 , ⋯ , i − 1 \boldsymbol\gamma_j = 0 \quad j = 1,\cdots,i-1 γj=0j=1,⋯,i−1。
(72) 式可简化为
Σ
x
u
i
=
λ
i
u
i
\Sigma_ {\boldsymbol x} \boldsymbol u_i = \boldsymbol\lambda_i \boldsymbol u_i
Σxui=λiui
即最优解
u
i
\boldsymbol u_i
ui为协方差矩阵
Σ
x
\Sigma_{\boldsymbol x}
Σx 第
i
i
i 个特征值
λ
i
\lambda_i
λi 对应的特征向量,此时的极值为
max
u
i
⊤
Σ
x
u
i
=
λ
i
u
i
⊤
u
i
=
λ
i
=
V
a
r
[
y
i
]
\text{max}\;\; \boldsymbol {u_i^{\top}} \boldsymbol\Sigma_x \boldsymbol u_i = \lambda_i \boldsymbol {u_i^{\top}} \boldsymbol u_i = \lambda_i = Var[y_i]
maxui⊤Σxui=λiui⊤ui=λi=Var[yi]
对于
Σ
x
\Sigma_{\boldsymbol x}
Σx 有重复特征根的情形亦如此,略。
由上述定理可知,随机变量
x
\boldsymbol x
x 的
d
d
d 个主元要优于一个主元,将所有的
d
d
d 个主元表示成一个向量
y
=
[
y
1
y
2
⋮
y
d
]
=
[
u
1
⊤
x
u
2
⊤
x
⋮
u
d
⊤
x
]
=
[
u
1
⊤
u
2
⊤
⋮
u
d
⊤
]
x
=
U
⊤
x
\boldsymbol{y}=\begin{bmatrix} y_1\\ y_2 \\ \vdots \\ y_d \end{bmatrix} =\begin{bmatrix} \boldsymbol{u}_1^\top\boldsymbol{x}\\ \boldsymbol{u}_2^\top\boldsymbol{x}\\ \vdots \\ \boldsymbol{u}_d^\top\boldsymbol{x}\\ \end{bmatrix} =\begin{bmatrix} \boldsymbol{u}_1^\top\\ \boldsymbol{u}_2^\top\\ \vdots \\ \boldsymbol{u}_d^\top\\ \end{bmatrix}\boldsymbol{x} =U^\top\boldsymbol{x}
y=
y1y2⋮yd
=
u1⊤xu2⊤x⋮ud⊤x
=
u1⊤u2⊤⋮ud⊤
x=U⊤x
其中
y
∈
R
d
,
U
∈
R
D
×
d
\boldsymbol y \in R^d,U \in R^{D\times d}
y∈Rd,U∈RD×d,此时
y
\boldsymbol y
y 的协方差矩阵可表示为
Σ
y
=
E
[
y
y
⊤
]
=
E
[
U
⊤
x
x
⊤
U
]
=
U
⊤
Σ
x
U
\Sigma_{\boldsymbol y} = E[\boldsymbol y \boldsymbol y^{\top}] = E[U^{\top}\boldsymbol x\boldsymbol x^{\top}U] = U^{\top} \Sigma_{\boldsymbol x} U
Σy=E[yy⊤]=E[U⊤xx⊤U]=U⊤ΣxU
满足
U
⊤
U
=
I
d
U^{\top}U = I_d
U⊤U=Id。
由线性代数知识可知,对于任意可对角化的矩阵 A A A,则存在由 A A A的特征向量组成的列表示的矩阵 V V V,有 Λ = V − 1 A V \boldsymbol\Lambda = V^{-1}AV Λ=V−1AV,而当矩阵 A A A是实对称半正定矩阵时,其特征值 λ i ≥ 0 \boldsymbol\lambda_i \ge 0 λi≥0,特征向量互相正交,且 V − 1 = V ⊤ V^{-1} = V^{\top} V−1=V⊤。因此,由于 Σ x \Sigma_x Σx是实对称正定矩阵,则方程 Σ y = U ⊤ Σ x U \Sigma_y = U^{\top} \Sigma_x U Σy=U⊤ΣxU中 U U U的列是协方差矩阵 Σ x \Sigma_x Σx的 d d d个特征向量组成。而 Σ y \Sigma_y Σy是一个对角矩阵,对角元为 Σ x \Sigma_x Σx的 d d d个特征值。因为我们的目标是极大化 y i \boldsymbol y_i yi的方差 V a r [ y i ] = λ i Var[\boldsymbol y_i] = \lambda_i Var[yi]=λi,所以我们的结论是协方差矩阵 Σ x \Sigma_x Σx的前 d d d个最大特征值对应的特征向量做为 U U U的列,即为目标的最优解,其极值则为 Σ y \Sigma_y Σy的对角元上 d d d个特征值。
3. 非零均值随机变量的主元
当
x
∈
R
D
\boldsymbol x \in R^D
x∈RD 有非零均值,则
x
\boldsymbol x
x 的
d
d
d 个不相关主元定义为
y
i
=
u
i
⊤
x
+
a
i
i
=
1
,
2
,
⋯
,
d
y_i = \boldsymbol {u_i^{\top}} \boldsymbol x + a_i \qquad i = 1,2, \cdots ,d
yi=ui⊤x+aii=1,2,⋯,d
满足
u
i
⊤
u
i
=
1
,
V
a
r
(
y
1
)
≥
V
a
r
(
y
2
)
≥
⋯
≥
V
a
r
(
y
d
)
>
0
\boldsymbol{u_i^{\top}} \boldsymbol u_i = 1,Var(\boldsymbol y_1) \ge Var(\boldsymbol y_2) \ge \cdots \ge Var(\boldsymbol y_d)>0
ui⊤ui=1,Var(y1)≥Var(y2)≥⋯≥Var(yd)>0
由于随机变量
y
i
y_i
yi 满足
E
[
y
i
]
=
0
cov
(
y
i
,
y
j
)
=
0
E
[
y
i
]
=
E
[
u
i
⊤
x
+
a
i
]
=
u
i
⊤
E
[
x
]
+
a
i
=
u
i
⊤
μ
x
+
a
i
=
0
i
=
1
,
2
,
⋯
,
d
\mathbb E[y_i] = 0 \\ \text{cov}(y_i,y_j) = 0 \\ \mathbb E[y_i] = \mathbb E[\boldsymbol{u_i^{\top}} \boldsymbol x + a_i] = \boldsymbol{u_i^{\top}} \mathbb E[\boldsymbol x] + \boldsymbol a_i = \boldsymbol{u_i^{\top}} \boldsymbol\mu_ x + a_i = 0 \qquad i = 1,2, \cdots ,d
E[yi]=0cov(yi,yj)=0E[yi]=E[ui⊤x+ai]=ui⊤E[x]+ai=ui⊤μx+ai=0i=1,2,⋯,d
因此
a
i
=
−
u
i
⊤
μ
x
a_i = - \boldsymbol{u_i^{\top}} \boldsymbol\mu_x
ai=−ui⊤μx
则
V
a
r
[
y
1
]
=
V
a
r
[
u
1
⊤
x
+
a
1
]
=
V
a
r
[
u
1
⊤
x
−
u
1
⊤
μ
x
]
=
V
a
r
[
u
1
⊤
(
x
−
μ
x
)
]
=
E
[
u
1
⊤
(
x
−
μ
x
)
(
x
−
μ
x
)
⊤
u
1
]
=
u
1
⊤
E
[
(
x
−
μ
x
)
(
x
−
μ
x
)
⊤
]
u
1
=
u
1
⊤
Σ
x
u
1
Var[y_1] = Var[\boldsymbol {u_1^{\top}} \boldsymbol x + a_1] = Var[\boldsymbol {u_1^{\top}} \boldsymbol x - \boldsymbol {u_1^{\top}} \boldsymbol\mu_x] =Var[\boldsymbol{u_1^{\top}} \left (\boldsymbol x - \boldsymbol\mu_x \right)] \\ = E[\boldsymbol{u_1^{\top}} (\boldsymbol x - \boldsymbol\mu_x) (\boldsymbol x - \boldsymbol\mu_x)^{\top} \boldsymbol u_1] = \boldsymbol {u_1^{\top}} E [(\boldsymbol x - \boldsymbol\mu_x) (\boldsymbol x - \boldsymbol\mu_x)^{\top} ] \boldsymbol u_1 = \boldsymbol{u_1^{\top}} \Sigma_{\boldsymbol x} \boldsymbol u_1
Var[y1]=Var[u1⊤x+a1]=Var[u1⊤x−u1⊤μx]=Var[u1⊤(x−μx)]=E[u1⊤(x−μx)(x−μx)⊤u1]=u1⊤E[(x−μx)(x−μx)⊤]u1=u1⊤Σxu1
则最优解
u
1
\boldsymbol u_1
u1 的计算可描述为
max
V
a
r
[
y
1
]
\text{max} \ Var[y_1]
max Var[y1]
即
max
u
1
u
1
⊤
Σ
x
u
1
u
1
⊤
u
1
=
1
\max_{\boldsymbol u_1} \boldsymbol {u_1^{\top}} \Sigma_x \boldsymbol u_1 \\ \boldsymbol{u_1^{\top}} \boldsymbol u_1 = 1
u1maxu1⊤Σxu1u1⊤u1=1
构造拉格朗日函数
L
(
u
1
)
=
u
1
⊤
Σ
x
u
1
+
λ
i
(
1
−
u
1
⊤
u
1
)
\mathcal{L}\ (\boldsymbol{u}_{1})=\boldsymbol {{u}_{1}^{\top}} {\Sigma}_ {\boldsymbol x} \boldsymbol {u}_{1}+\boldsymbol\lambda_{i}\left(1-\boldsymbol {{u}_{1}^{\top}} \boldsymbol {u}_{1}\right)
L (u1)=u1⊤Σxu1+λi(1−u1⊤u1)
置拉格朗日函数偏导数为0
∂
L
(
u
1
)
∂
u
1
=
2
Σ
x
u
1
−
2
λ
1
u
1
=
0
\frac{\partial \mathcal{L} (\boldsymbol u_{1})}{\partial \boldsymbol {u}_{1}}=2 {\Sigma}_{x} \boldsymbol {u}_{1}-2 \boldsymbol\lambda_{1} \boldsymbol {u}_{1} = 0
∂u1∂L(u1)=2Σxu1−2λ1u1=0
得
Σ
x
u
1
=
λ
1
u
1
\Sigma_ x \boldsymbol u_1 = \lambda_1 \boldsymbol u_1
Σxu1=λ1u1
由此可知
λ
1
\lambda_1
λ1和
u
1
\boldsymbol u_1
u1分别为协方差矩阵
Σ
x
=
(
x
−
μ
)
(
x
−
μ
)
⊤
\Sigma_{\boldsymbol x} = (\boldsymbol x - \boldsymbol\mu ) (\boldsymbol x - \boldsymbol\mu )^{\top}
Σx=(x−μ)(x−μ)⊤ 的最大特征值与其对应的特征向量。对于地
i
i
i个最优解
u
i
\boldsymbol u_i
ui的解与前面定理的证明完全一致。
4. 零均值随机变量的样本主元
在实际应用中,我们并不知道随机变量的协方差矩阵,只能由样本点进行估计,对于独立同分布且期望为0的样本
{
x
i
}
i
=
1
N
\left \{ \boldsymbol x_i \right \} _{i=1}^N
{xi}i=1N,构造样本矩阵
X
=
[
x
1
,
x
2
,
⋯
,
x
N
]
\boldsymbol X=[\boldsymbol x_1,\boldsymbol x_2, \cdots ,\boldsymbol x_N]
X=[x1,x2,⋯,xN],其样本协方差为
Σ
N
=
1
N
∑
i
=
1
N
x
i
x
i
⊤
=
1
N
X
X
⊤
\Sigma_N = \frac{1}{N} \sum_{i=1}^N \boldsymbol x_i \boldsymbol{x_i^{\top}} = \frac{1}{N} \boldsymbol X \boldsymbol{X^{\top}}
ΣN=N1i=1∑Nxixi⊤=N1XX⊤
则
d
d
d个样本主元为
y
i
=
u
^
i
⊤
x
i
=
1
,
2
,
⋯
,
d
y_i = \boldsymbol{\hat{u}_i^{\top}} \boldsymbol x \qquad i = 1,2, \cdots ,d
yi=u^i⊤xi=1,2,⋯,d
其中
{
u
i
}
i
=
1
d
\left \{ \boldsymbol u_i \right \} _{i=1}^d
{ui}i=1d为
Σ
^
N
=
1
N
X
X
⊤
\hat\Sigma_N = \frac{1}{N} \boldsymbol X \boldsymbol{X^{\top}}
Σ^N=N1XX⊤或
X
X
⊤
\boldsymbol X \boldsymbol{ X^{\top} }
XX⊤的前
d
d
d个特征向量。
由于
X
X
⊤
∈
R
D
×
D
\boldsymbol X \boldsymbol{X^{\top}} \in \boldsymbol R^{D\times D}
XX⊤∈RD×D是一个非常大的矩阵,所以我们可以利用
X
\boldsymbol X
X的奇异值获得最优解,即
X
=
U
x
Σ
x
V
x
⊤
X = U_x \Sigma_x V_x^{\top}
X=UxΣxVx⊤
y = [ y 1 y 2 ⋮ y d ] = [ u 1 ⊤ x u 2 ⊤ x ⋮ u d ⊤ x ] = [ u 1 ⊤ u 2 ⊤ ⋮ u d ⊤ ] x = U ⊤ x \boldsymbol{y}=\begin{bmatrix} y_1\\ y_2 \\ \vdots \\ y_d \end{bmatrix} =\begin{bmatrix} \boldsymbol{u}_1^\top\boldsymbol{x}\\ \boldsymbol{u}_2^\top\boldsymbol{x}\\ \vdots \\ \boldsymbol{u}_d^\top\boldsymbol{x}\\ \end{bmatrix} =\begin{bmatrix} \boldsymbol{u}_1^\top\\ \boldsymbol{u}_2^\top\\ \vdots \\ \boldsymbol{u}_d^\top\\ \end{bmatrix}\boldsymbol{x} =U^\top\boldsymbol{x} y= y1y2⋮yd = u1⊤xu2⊤x⋮ud⊤x = u1⊤u2⊤⋮ud⊤ x=U⊤x
5. PCA 降维案例
We will first demonstrate PCA on a 13-dimensional dataset, by loading wine dataset from sklearn, see info here.
This dataset contains chemical analysis of N=178 different wines by three different cultivators.
The analysis contains the folowing measurements:
Alcohol
Malic acid
Ash
Alcalinity of ash
Magnesium
Total phenols
Flavanoids
Nonflavanoid phenols
Proanthocyanins
Colour intensity
Hue
OD280/OD315 of diluted wines
Proline
So overall, we have N=178 data points, lying in
R
D
\mathbb{R}^{D}
RD, with D=13. We stack all points together into a matrix X_wine
∈
R
D
×
N
\in \mathbb{R}^{D\times N}
∈RD×N.
We have labels 0,1, or 2 for each wine (clutivator). The true labels are given in L_wine.
We want to see whether PCA can be helpful in the unsupervised task of clustering the 178 wines.
We start by loading the dataset, and printing the first 5 data points, just to get a general impression.
# 主成分分析算法
# 输入:
# X: 数据矩阵大小为 n*D,每一行为 D 维向量(样本点)
# 参数:
# dims_remain: 降维后保留的维数
# with_std: 是否进行标准化操作,默认为进行标准化
# 返回:
# X_reduction: 降维后的数据,数据矩阵大小为 n*d,每一行为 d 维向量(样本点)
from numpy.linalg import svd
from sklearn.preprocessing import StandardScaler
class PCA_PC:
def __init__(self,dims_remain=2,with_std=True):
self.dims_remain = dims_remain
self.with_std = with_std
def fit_transform(self,X):
if self.with_std:
ss = StandardScaler() # 此对象针对的是模式矩阵
ss.fit(X)
XS = ss.transform(X)
U,_,_ = svd(XS.T) # 特征值分解函数的输入是模式矩阵的转置,输出 U 的每一列为新坐标轴
X_reduction = XS@U[:,0:self.dims_remain]
else:
U,_,_ = svd(X.T)
X_reduction = X@U[:,0:self.dims_remain]
return X_reduction
调用函数
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_wine
if __name__ == '__main__':
X_wine, L_wine = load_wine(return_X_y=True)
np.set_printoptions(suppress=True)
model1 = PCA_PC(dims_remain=2,with_std=False)
X_reduct1 = model1.fit_transform(X_wine)
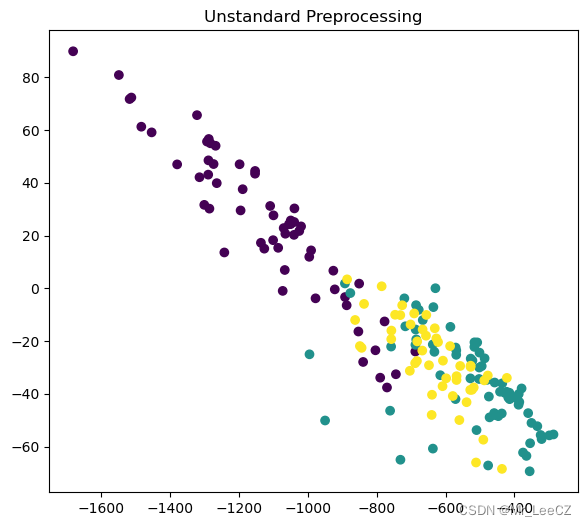
plt.figure(figsize=(15,6))
plt.subplot(121),plt.scatter(X_reduct1[:,0], X_reduct1[:,1], c=L_wine)
plt.title('Unstandard Preprocessing')
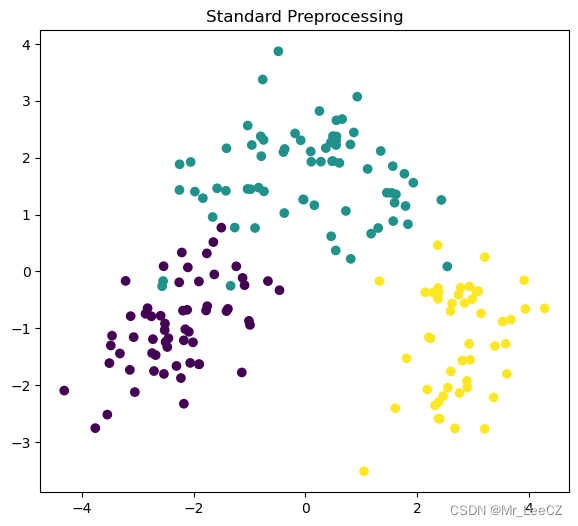
model2 = PCA_PC(dims_remain=2,with_std=True)
X_reduct2 = model2.fit_transform(X_wine)
plt.figure(figsize=(15,6))
plt.subplot(121),plt.scatter(X_reduct2[:,0], X_reduct2[:,1], c=L_wine)
plt.title('Standard Preprocessing')
plt.show()