目录
一、概念
二、实现
非递归删除
递归删除
三、总结
一、概念
二叉搜索树(BST,Binary Search Tree)
也称二叉排序树,二叉查找树
二叉搜索树:一棵二叉树,可以为空,如果不为空,满足以下性质:
1. 非空左子树的所有键值小于其根节点的键值
2. 非空右子树的所有键值大于其根节点的键值
3. 左右子树都为二叉搜索树
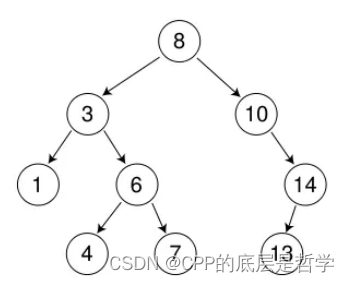
二、实现
//
// Created by yangzilong on 2022/10/30.
//
#ifndef STL_BINARYSEARCHTREE_H
#define STL_BINARYSEARCHTREE_H
#include<iostream>
template <typename K>
struct BSTreeNode
{
BSTreeNode(const K& key)
:_key(key), _left(nullptr), _right(nullptr)
{ }
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
};
template <typename K>
class BinarySearchTree {
typedef BSTreeNode<K> Node;
private:
Node* _root = nullptr;
public:
~BinarySearchTree()
{
_Destroy(_root);
}
BinarySearchTree() = default;
BinarySearchTree(const BinarySearchTree<K>& t)
{
_root = _Copy(t._root);
}
BinarySearchTree<K>& operator=(BinarySearchTree<K> t)
{
std::swap(_root, t._root);
return *this;
}
private:
Node* _Copy(Node* root)
{
if(root == nullptr)
return nullptr;
Node* newNode = new Node(root->_key);
newNode->_left = _Copy(root->_left);
newNode->_right = _Copy(root->_right);
return newNode;
}
void _Destroy(Node* root)
{
if(root == nullptr)
return;
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
public:
// 非递归
bool Insert(const K& key) {
// 空树
if (_root == nullptr) {
_root = new Node(key);
return true;
}
Node *cur = _root;
Node *parent = nullptr;
while (cur) {
if (cur->_key < key) {
parent = cur;
cur = cur->_right;
} else if (cur->_key > key) {
parent = cur;
cur = cur->_left;
} else {
return false; // 已经存在了
}
}
if (key > parent->_key) {
parent->_right = new Node(key);
} else {
parent->_left = new Node(key);
}
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while(cur)
{
if(key > cur->_key)
{
cur = cur->_right;
}
else if(key < cur->_key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key) {
Node *cur = _root;
Node *parent = _root;
while (cur) {
if (key > cur->_key) {
parent = cur;
cur = cur->_right;
} else if (key < cur->_key) {
parent = cur;
cur = cur->_left;
} else {
// edition 2
if(cur->_left == nullptr)
{
if(parent->_left == cur)
{
parent->_left = cur->_right;
delete cur;
}
else
{
parent->_right = cur->_right;
delete cur;
}
}
else if(cur->_right == nullptr)
{
if(parent->_left == cur)
{
parent->_left = cur->_left;
delete cur;
}
else
{
parent->_right = cur->_left;
delete cur;
}
}
else
{
// 要删除结点的左右均不为空
// 去删除结点的右子树中找最小值,替换法删除
Node* min = cur->_right;
Node* minParent = cur;
while(min->_left)
{
minParent = min;
min = min->_left;
}
std::swap(cur->_key, min->_key);
if(min == minParent->_right)
minParent->_right = min->_right;
else
minParent->_left = min->_right;
delete min;
}
return true;
// old
// if (cur->_left == nullptr && cur->_right == nullptr) {
// // 叶子节点,直接删除
// if (parent->_left->_key == key) {
// delete parent->_left;
// parent->_left = nullptr;
// } else {
// delete parent->_right;
// parent->_right = nullptr;
// }
// } else if (cur->_left != nullptr && cur->_right != nullptr) {
// // 找右子树的最小值,和cur交换值
// Node *minParent = cur;
// Node *min = cur->_right; // child一定不为nullptr
// while (min->_left) {
// minParent = min;
// min = min->_left;
// }
// std::swap(cur->_key, min->_key);
// if (minParent == cur) {
// minParent->_right = min->_right; // 此时child->_left一定为nullptr
// delete min;
// } else {
// // 此时child和parent_2的关系一定是左子树和父节点
// minParent->_left = min->_right;
// delete min;
// }
// } else {
// Node *child = nullptr;
// if (cur->_right != nullptr) {
// child = cur->_right;
// } else {
// child = cur->_left;
// }
// if (parent->_left != nullptr && parent->_left->_key == key) {
// delete parent->_left;
// parent->_left = child;
// } else {
// delete parent->_right;
// parent->_right = child;
// }
// }
// return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
std::cout<<std::endl;
}
private:
void _InOrder(Node* root)
{
if(root == nullptr)
return;
_InOrder(root->_left);
std::cout<<root->_key<<" ";
_InOrder(root->_right);
}
// 递归
public:
bool Find_R(const K& key)
{
// 最多找h次,h为树的高度。
return _Find_R(_root, key);
}
bool Insert_R(const K& key)
{
return _Insert_R(_root, key);
}
bool Erase_R(const K& key)
{
return _Erase_R(_root, key);
}
private:
bool _Erase_R(Node*& root, const K& key)
{
if(root == nullptr)
{
// 不存在
return false;
}
if(key < root->_key)
{
return _Erase_R(root->_left, key);
}
else if(key > root->_key)
{
return _Erase_R(root->_right, key);
}
else
{
// 要删除的就是这个root,这个root实际上是父节点结构体里的right or left指针的别名!!!!!
if(root->_left == nullptr) {
Node* del = root;
root = root->_right;
delete del;
}
else if(root->_right == nullptr) {
Node *del = root;
root = root->_left;
delete del;
}
else
{
Node* minParent = root;
Node* min = root->_right;
while(min->_left)
{
minParent = min;
min = min->_left;
}
std::swap(root->_key, min->_key);
// 上方交换时,root的key一定比min的key小,因为min在root的右子树中。
// 此时交换完,root的key在右子树中一定符合二叉搜索树。
// 并且下方递归调用时,一定会走左为空的情况。
return _Erase_R(root->_right, key);
// if(minParent->_left == min)
// {
// minParent->_left = min->_right;
// }
// else
// {
// minParent->_right = min->_right;
// }
// delete min;
}
return true;
}
}
bool _Insert_R(Node*& root, const K& key)
{
if(root == nullptr)
{
root = new Node(key);
return true;
}
if(key < root->_key)
{
// 这里是把结构体里的指针成员传过去,参数用引用接收,改变参数就是改变这里结构体的指针成员。
return _Insert_R(root->_left, key);
}
else if(key > root->_key)
{
// 这里是把结构体里的指针成员传过去,参数用引用接收,改变参数就是改变这里结构体的指针成员。
return _Insert_R(root->_right, key);
}
else
{
return false;
}
}
// bool _Insert_R(Node* root, const K& key)
// {
// if(root == nullptr)
// {
// _root = new Node(key);
// return true;
// }
// if(root->_key < key && root->_right == nullptr)
// {
// root->_right = new Node(key);
// return true;
// }
// else if(root->_key > key && root->_left == nullptr)
// {
// root->_left = new Node(key);
// return true;
// }
// else if(root->_key > key)
// {
// return _Insert_R(root->_left, key);
// }
// else if(root->_key < key)
// {
// return _Insert_R(root->_right, key);
// }
// else
// {
// return false;
// }
// }
bool _Find_R(Node* root, const K& key)
{
if(root == nullptr)
return false;
if(root->_key > key)
{
return _Find_R(root->_left, key);
}
else if(root->_key < key)
{
return _Find_R(root->_right, key);
}
else
{
return true;
}
}
};以上包含二叉搜索树的递归版与非递归版的插入,删除,查找。以及拷贝构造和析构的实现。
唯一值得注意的就是删除了
非递归删除
先找到该结点,同时注意要记录要删除结点的父节点。
分情况:
1. 要删除结点的左右为空,即叶子结点
2. 要删除结点的左为空
3. 要删除结点的右为空
4. 要删除结点的左右都为空
1可以和2或3其中之一合并。
若要删除结点(cur)的左为空,则将cur的右赋值给parent的左或右(取决于cur是parent的左还是右)
若要删除结点(cur)的右为空,则将cur的左赋值给parent的左或右(取决于cur是parent的左还是右)
// 要删除结点的左右均不为空
// 去删除结点的右子树中找最小值,替换法删除
Node* min = cur->_right;
Node* minParent = cur;
while(min->_left)
{
minParent = min;
min = min->_left;
}
std::swap(cur->_key, min->_key);
if(min == minParent->_right)
minParent->_right = min->_right;
else
minParent->_left = min->_right;
delete min;若要删除结点(cur)的左右均不为空,则查找cur的右子树中的最小结点(min),即图中的while循环),采用交换法,将cur的key和min的key交换(此时min的值放在cur的位置是符合二叉搜索树的性质的),此时要删除的结点就转换为了min。
注意,此时要判断,min是cur的右结点还是右节点的左子树的某个结点。也就是while循环有没有执行。

转换为上图,也就是
若删除3(cur),则4是min,min是minparent的左。
若删除8(cur),则10是min,min是minparent的右。
不管怎样,min的左一定为空,直接将min的右(空or非空)赋值给min的左或右即可(取决于min是minparent的左还是右)
递归删除
bool _Erase_R(Node*& root, const K& key)
{
if(root == nullptr)
{
// 不存在
return false;
}
if(key < root->_key)
{
return _Erase_R(root->_left, key);
}
else if(key > root->_key)
{
return _Erase_R(root->_right, key);
}
else
{
// 要删除的就是这个root,这个root实际上是父节点结构体里的right or left指针的别名!!!!!
if(root->_left == nullptr) {
Node* del = root;
root = root->_right;
delete del;
}
else if(root->_right == nullptr) {
Node *del = root;
root = root->_left;
delete del;
}
else
{
Node* minParent = root;
Node* min = root->_right;
while(min->_left)
{
minParent = min;
min = min->_left;
}
std::swap(root->_key, min->_key);
// 上方交换时,root的key一定比min的key小,因为min在root的右子树中。
// 此时交换完,root的key在右子树中一定符合二叉搜索树。
// 并且下方递归调用时,一定会走左为空的情况。
return _Erase_R(root->_right, key);
// if(minParent->_left == min)
// {
// minParent->_left = min->_right;
// }
// else
// {
// minParent->_right = min->_right;
// }
// delete min;
}
return true;
}
}除了是基于递归实现的,这里的基本原理和非递归一样,只是在交换完cur和min的key之后,直接在cur的右子树中删除key即可(此时key在min结点中)。最终会递归到左子树为空的情况,因为min->left == nullptr
三、总结
若二叉搜索树接近完全二叉树,也就是高度接近log(N),则二叉搜索树的效率会很高。
若二叉搜索树的构建过程中,元素有序或者接近有序,则BST的查找,删除,插入的效率都会很低,接近O(N),故引出AVL树,红黑树来控制搜索树的高度。