1. 原始BWO算法

BWO算法的种群初始化和大多数智能算法相同，即随机产生搜索空间中的若干候选解，此处不再赘述。

1.1 勘探阶段

作者考虑白鲸的游动行为，将其设计为BWO算法的勘探阶段。白鲸可以在不同的姿势下进行社会性行为，例如两只白鲸可以以同步或者镜像的方式紧密地游泳。白鲸的位置更新公式为：

1.2 开发阶段

BWO算法开发阶段模拟的是白鲸的捕食行为。白鲸通过分享彼此的位置信息来捕食，因此考虑最佳个体和其他个体对位置更新的影响。在BWO的开发阶段，引入了Levy飞行策略来增强收敛性。此阶段的数学模型为：

1.3 鲸落阶段

白鲸要么迁徙到其他地方，要么发生鲸落坠入深海。为了保证种群大小不变，使用白鲸的当前位置和鲸落下坠的步长来建立位置更新公式：

2. 改进白鲸优化算法

2.1 Tent映射种群初始化

此为常用策略，此处不再赘述。

2.2 反向学习策略

反向学习是智能计算领域一种新技术，它同时评估原始解决方案和基于反向的解决方案，并选择更好的解决方案。
若$x\in [a,b]$之间的任意实数，则$x$的基于反向学习的数如下：

可见，正向解和反向解是位于搜索空间的两侧，因此，引入此策略，可以扩大搜索区域，增强全局搜索能力。

3. 部分代码展示

%% 反向学习
% 输入
% X：种群个体 
% VarMin：下限  
% VarMax：上限
% 输出
% newpop： 变异后的种群个体

function newpop=reverse_learning(X,lowerbound,upperbound,fobj)

%边界处理
upperbound=upperbound.*ones(size(X,1),size(X,2));
lowerbound=lowerbound.*ones(size(X,1),size(X,2));

%%  反向学习主代码
X_new=rand(size(X,1),size(X,2)).*(upperbound+lowerbound)-X;

%处理超越边界方法为游离,并非顶值
for i=1:size(X_new,1)
    for j=1:size(X_new,2)
        if X_new(i,j)>upperbound(i,j)
            X_new(i,j)=(upperbound(i,j)-lowerbound(i,j))*rand()+lowerbound(i,j);
        elseif X_new(i,j)<lowerbound(i,j)
            X_new(i,j)=(upperbound(i,j)-lowerbound(i,j))*rand()+lowerbound(i,j);
        end
    end
end

X_new=[X;X_new];
for i=1:size(X_new,1)   
    fitness(i)=fobj(X_new(i,:));
end
%按适应度从小到大排序
[~,index]=sort(fitness);
newpop=X_new(index(1:size(X,1)),:);

end

4. 仿真结果展示

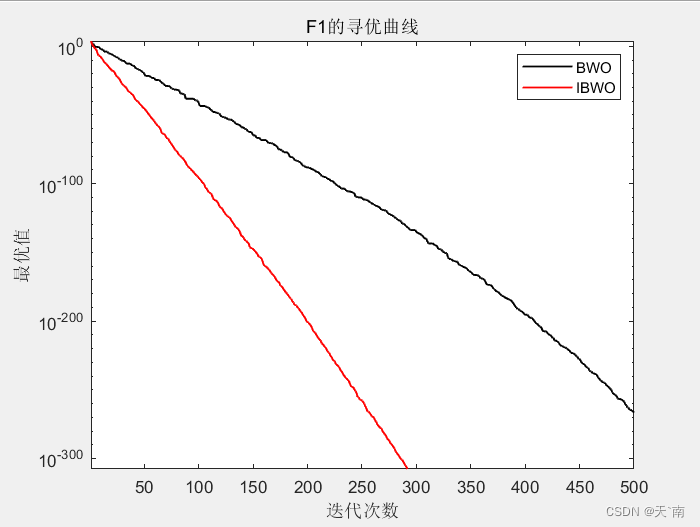
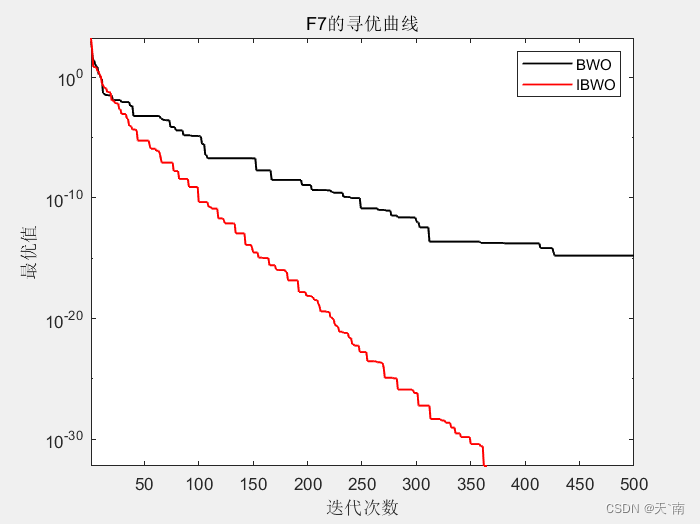
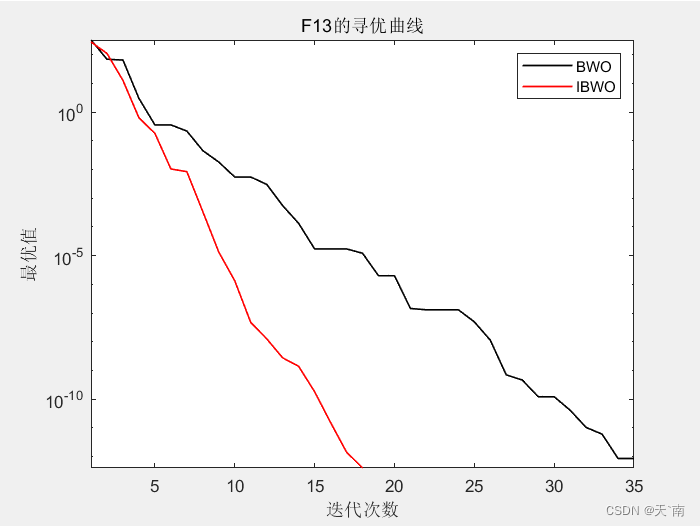
5. 资源获取

A资源获取说明