为什么有龙贝格算法:
龙贝格算法是一种数值积分方法,用于计算定积分的数值近似值。它是基于复合梯形法和复合辛普森法的推广和拓展,可以达到更高的精度。相较于复合梯形法和复合辛普森法,龙贝格算法的收敛速度更快,且误差更小,因此在计算积分时更加精确。此外,龙贝格算法具有简单的递推公式和容易实现的特点,因此被广泛应用于实际计算中。

龙贝格算法:
龙贝格算法是一种基于复合梯形公式的数值积分算法,用于计算定积分的近似值。它是一种自适应算法,通过逐步增加划分数目,逐步逼近精确解。
算法的基本思想是:首先用复合梯形公式计算出一组初始积分值,然后通过加权平均、递归和外推的方式逐步提高积分精度,最终得到一个更加准确的积分近似值。
具体而言,假设我们要计算函数 $f(x)$ 在区间 $[a,b]$ 上的定积分 $I=\int_{a}^{b}f(x)dx$。将区间 $[a,b]$ 划分成 $2^n$ 个小区间,并将每个小区间的长度设为 $h=(b-a)/2^n$。则复合梯形公式的积分近似值为:
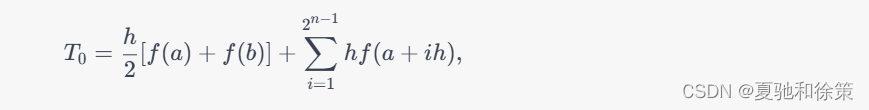
其中 $T_0$ 是零阶逼近值,$h$ 是步长,$i$ 是整数。
然后,我们可以通过递归求得更高阶的逼近值,递推公式为:

其中 $T_{m,k}$ 表示使用 $2^m$ 个区间时,第 $k$ 个逼近值,$m$ 表示迭代次数,$k$ 表示在第 $m$ 次迭代中从左向右第 $k$ 个逼近值。
通过不断迭代,我们可以得到更加准确的积分近似值,同时也可以得到一些误差估计值。
龙贝格算法的优点在于,它可以自适应地调整步长和划分数目,使得积分精度更高,同时也可以更好地控制计算误差。
 龙贝格序列:
龙贝格序列:
龙贝格序列是用于龙贝格算法的一个数列,通常表示为 $R_{m,n}$,其中 $m$ 表示使用 $2^m$ 个子区间进行数值积分,$n$ 表示使用 $n$ 阶的复合梯形公式。龙贝格序列的计算通过一个递归的过程完成。
首先,使用 $n=1$ 阶的复合梯形公式计算 $R_{0,1}$,即将区间 $[a,b]$ 平分成两部分,计算每一部分上的梯形面积,然后将它们相加。此时,$R_{0,1}$ 就是数值积分的第一个近似值。
然后,利用递推公式:
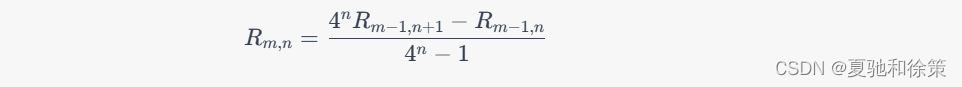
计算 $R_{1,1}$,$R_{2,1}$,直到 $R_{k,k}$,其中 $k$ 取决于需要达到的精度。每一步通过增加阶数 $n$ 来提高精度。最终的数值积分值近似等于 $R_{k,k}$。值得注意的是,递推公式中的 $4^n$ 出现是因为龙贝格算法的核心是基于 Richardson 外推方法,其系数为 $4^n$。
通过递推公式,每次将阶数增加 $1$,可以使用相同的区间数量计算出更高阶的复合梯形公式,从而提高数值积分的精度。在计算龙贝格序列时,需要注意一些细节,如选择合适的递推次数、判断收敛性等等。

外推方法
外推法是一种用于提高数值积分精度的方法,其基本思想是通过使用多个递推公式和 Richardson 外推来不断提高积分精度。外推法通常可以使用更低阶的方法递推出更高阶的方法,从而大幅减少计算量和存储需求。
在数值积分中,我们通常使用低阶公式计算积分,然后使用外推法将其逐步提高精度。其中,最常用的外推法是 Richardson 外推,它基于一种类似于牛顿-科茨公式的递推公式。对于任意一个具有代数精度 $p$ 的数值积分公式 $T(h)$,Richardson 外推公式可以表示为:

其中,$R_{j,k}$ 表示使用步长为 $h_j = h/2^j$ 的 $2^{k-1}+1$ 个点计算得到的数值积分近似值,$R_{j,0} = T(h_j)$。外推过程中,$j$ 代表递推的层数,$k$ 代表 Richardson 外推的阶数。
通过不断增加 $j$ 的值,可以逐步提高数值积分的精度,直到满足所需的误差精度为止。
总结:
下面是龙贝格算法的重点、难点和易错点的总结:
重点:
- 龙贝格算法是一种外推算法,通过递推得到更高精度的数值积分结果。
- 龙贝格算法基于变步长梯形法,通过逐步缩小步长来逼近真实值。
- 龙贝格算法中的递推公式是核心,掌握递推公式的推导和使用是理解和应用该算法的关键。
- 龙贝格算法的收敛速度很快,通常在5次左右即可达到较高的精度。
难点:
- 龙贝格算法的递推公式较为复杂,需要理解和掌握多个系数的含义和作用。
- 龙贝格算法在计算中需要保留多个中间结果,需要注意数值计算中的舍入误差和精度损失。
易错点:
- 在使用龙贝格算法时,需要选择合适的步长和精度要求,否则可能会导致计算结果不准确。
- 龙贝格算法对于函数奇异性较强的情况效果不佳,此时需要考虑其他数值积分算法。
- 在实际计算中,需要注意避免除以0等错误,同时也需要注意数值溢出等问题。