最长公共子串
- 二分方法
- 字符串哈希的复习
- 字符串哈希 如何理解
- 二分代码
- dp方法
- 字符串str1中以第i个字符为结尾的子串 与字符串str2中以第i个字符为结尾的子串的连续公共子串
- 二维
- 一维优化
二分方法
- 由于这个题是要求求子串,而子串是连续的一段,所以用二分长度,找到最长的公共子串长度即可
- 那么用二分,我们就需要比较上下两个字符串,怎么对比两个字符串呢?经过演算,比较好的方法就是,把两个字符串,二分长度的时候,都把相应的字符串丢到 map里,当进行第一个字符串,把长度为x的子串丢到map后,再次把第二个字符串丢进去,如果出现重复,那么返回true,都没重复返回false
- 但是在map中会进行字符串比较,这个效率比较低,所以用 字符串哈希,把字符串的子串用 数字表示,这样在map里比较时,就会更方便
- 出现数字,把数字转成 两个字符串分别转成各自固定特殊符号,这样就不会重复
字符串哈希的复习
原题链接
字符串哈希 如何理解
首先我们理解在 123456中 如何取出456
我们把每个位置上的分别对应求出相应位置的总和
位置
1 ——》1
2 ——》12
3 ——》123
4 ——》 1234
5 ——》12345
6 ——》123456
那么我们把 123456 - 123*100 = 456
字符串也如此
ABCDEF
位置
1——》对应A的数字 同理如下即可
#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5+5,P = 131;//131 13331
ULL h[N],p[N];
// h[i]前i个字符的hash值
// 字符串变成一个p进制数字,体现了字符+顺序,需要确保不同的字符串对应不同的数字
// P = 131 或 13331 Q=2^64,在99%的情况下不会出现冲突
// 使用场景: 两个字符串的子串是否相同
ULL query(int l,int r){
return h[r] - h[l-1]*p[r-l+1];
}
int main(){
int n,m;
cin>>n>>m;
string x;
cin>>x;
//字符串从1开始编号,h[1]为前一个字符的哈希值
p[0] = 1;
h[0] = 0;
for(int i=0;i<n;i++){
p[i+1] = p[i]*P;
h[i+1] = h[i]*P +x[i]; //前缀和求整个字符串的哈希值
}
while(m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if(query(l1,r1) == query(l2,r2)) printf("Yes\n");
else printf("No\n");
}
return 0;
}
二分代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;
typedef unsigned long long ULL;
const int N = 20010, P = 131;
int n, m;
char str[N];
ULL p[N], h[N];
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
bool check(int mid)
{
unordered_set<ULL> hash;
for (int i = 1; i + mid - 1 <= n; i ++ )
hash.insert(get(i, i + mid - 1));
for (int i = n + 1; i + mid - 1 <= n + m; i ++ )
if (hash.count(get(i, i + mid - 1)))
return true;
return false;
}
int main()
{
scanf("%s", str + 1);
n = strlen(str + 1);
scanf("%s", str + n + 1);
m = strlen(str + n + 1);
p[0] = 1;
for (int i = 1; i <= n + m; i ++ )
{
p[i] = p[i - 1] * P;
char c = str[i];
if (isdigit(c))
{
if (i <= n) c = '#';
else c = '$';
}
h[i] = h[i - 1] * P + c;
}
int l = 0, r = min(n, m);
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
printf("%d\n", r);
return 0;
}
作者:yxc
链接:https://www.acwing.com/activity/content/code/content/6308090/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
dp方法
字符串str1中以第i个字符为结尾的子串 与字符串str2中以第i个字符为结尾的子串的连续公共子串
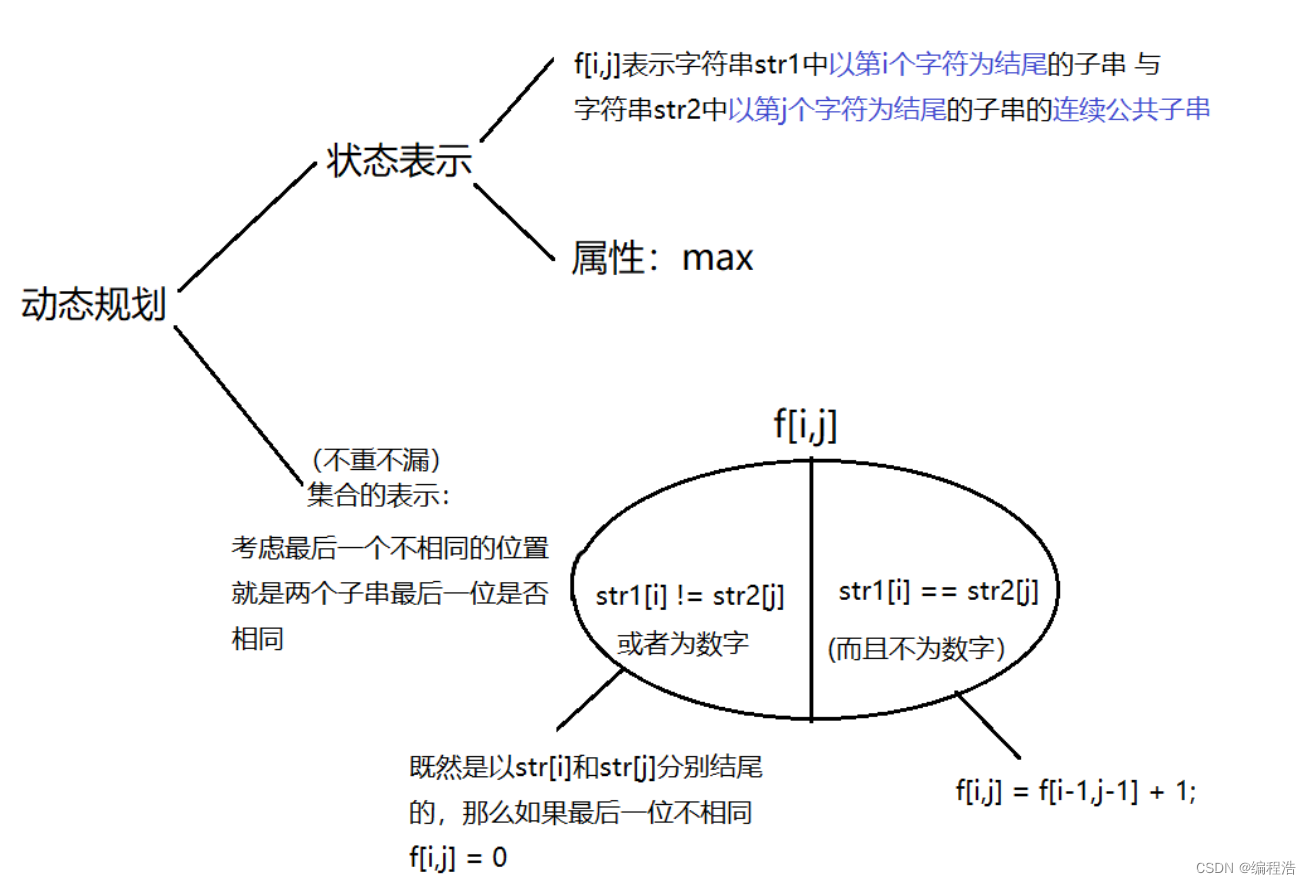
二维
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
char str1[N], str2[N];
int f[N][N];//注意空间限制为256MB,即为2^(8 + 20) = 2^28个字节,
//而一个int型变量占4个字节,那么最多有2^26个int变量,大约为64000000个变量,而此时定义f[N][N]最多有大于1e8个变量,会爆内存
//更何况还有存字符串的空间
int main()
{
cin >> str1 + 1 >> str2 + 1;
int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);
int res = 0;
for (int i = 1; i <= len1; i++)
{
//如果最后一位为数字
if (str1[i] >= '0' && str1[i] <= '9')
{
for (int j = 1; j <= len2; j++)
f[i][j] = 0;
continue;
}
for (int j = 1; j <= len2; j++)
{
//如果最后一位相同且不为数字
if (str1[i] == str2[j])
f[i][j] = f[i - 1][j - 1] + 1;
else f[i][j] = 0;
res = max(res, f[i][j]);
}
}
cout << res << endl;
return 0;
}

一维优化
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
char str1[N], str2[N];
int f[N];
int main()
{
cin >> str1 + 1 >> str2 + 1;
int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);
int res = 0;//用于保存答案
for (int i = 1; i <= len1; i++)
{
//如果最后一位为数字
if (str1[i] >= '0' && str1[i] <= '9')
{
for (int j = 1; j <= len2; j++)
f[j] = 0;
continue;
}
for (int j = len2; j >= 1; j--)
{
//如果最后一位相同且不为数字
if (str1[i] == str2[j])
f[j] = f[j - 1] + 1;
else f[j] = 0;
res = max(res, f[j]);
}
}
cout << res << endl;
return 0;
}
作者:a_zi_ge
链接:https://www.acwing.com/solution/content/185166/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。