试验设计必须遵循以下原则:重复、随机、局部控制。
重复即每个处理都要有至少2个试验单位,目的是估计试验误差,降低试验误差。若只有1个观测值,无法估计试验误差。平均数抽样误差估计值大小与重复次数的平方成反比,适当提高重复次数课降低试验误差,但重复次数过多,试验动物也将增多,初始条件难达成一致,不一定降低误差。若初始条件差异大,可多重复几次。
随机即随机分组,避免主观倾向,排除非实验因素的影响,目的是获得无偏的误差估计。
局部控制指当试验环境或试验单位差异大时,仅靠重复与随机无法将试验环境与试验单位误差所引起的异变从试验误差中分离。因此,可将整个试验环境或试验单位分成若干小环境或小组,每个小环境或小组内使得非处理因素尽量一致,达成局部一致。
1.完全随机试验
例:现有同体况绵羊18只,用随机数字法将其分为甲乙两组。
例:现有同体况仔猪18头,用随机数字法将其分为甲乙丙三组。
优点:设计容易,适用于实验条件、动物误差较小的场合;统计分析简单。
缺点:未有局部控制原则,非试验因素影响被归入试验误差,试验误差大,精度低;试验环境与动物差异大时,此法不宜。
2.随机单位组设计
现将同初始条件的试验动物归为一个单位组,每个单位组内的动物数等于处理数,然后将各单位组的试验动物独立随机分入各处理组,再按组实施不同处理。
例:五种草药A1-A5,从4头母猪所产的4窝仔猪中,每窝选取性别相同、体重接近的仔猪各5头,组成4个单位组,将每个单位组的5头仔猪独立随机分组
如:
| 添加剂 | 单位组(窝) | |||
| B1 | B2 | B3 | B4 | |
| A1 | 4 | 6 | 14 | 20 |
| A2 | 2 | 10 | 12 | 19 |
| A3 | 5 | 7 | 13 | 17 |
| A4 | 3 | 8 | 15 | 16 |
| A5 | 1 | 9 | 11 | 18 |
优点:设计与分析简单;体现了试验设计三原则,能将单位组间的变异从试验误差中分离,有效降低试验误差,精度较高;加大了处理组之间的可比性。
缺点:处理数过多时动物的供应数也会变多,初始条件难以控制一致,一般不超过20.
配对设计是处理数为2的随机单位组设计,优点是结果分析简单,误差一般比非配对设计小,但对试验动物要求严。
3.拉丁方设计
从横向与纵向进行局部控制,比随机单位组设计多了一个单位组的设计。在拉丁方设计中,每一行或每一列均是一个单位组,每个处理在每一行或每一列中只出现一次。
常见拉丁方有3*3、4*4、5*5、6*6阶,须对表查询。
例,为研究五种温度A-E对蛋鸡产蛋量的影响,有5个鸡舍5个鸡群参试,鸡群的产蛋期分为5期。因为鸡群与产蛋期的不同对产蛋量影响大,因此采用拉丁方设计,把鸡群与产蛋期作为单位组设置,以消除这两个单位组所产生的的系统误差对试验的影响。
| 产蛋期 | 鸡群 | ||||
| 一 | 二 | 三 | 四 | 五 | |
| X1 | D(23) | E(21) | A(24) | B(21) | C(19) |
| X2 | A(22) | C(20) | E(20) | D(21) | B(22) |
| X3 | E(20) | A(25) | B(26) | C(22) | D(23) |
| X4 | B(25) | D(22) | C(25) | E(21) | A(23) |
| X5 | C(19) | B(20) | D(24) | A(22) | E(19) |
优点:精确性高;实验结果分析简便;
缺点:横行与直列的处理数要一致,试验处理数与试验处理的重复数必须一致,故处理数收到限制,过少则重复少,影响灵敏度,过多则重复多,工作量大,同一单位组内试验动物初始条件难以控制一致。因此一般选择5-8个处理。
4.交叉设计
在同一试验中将实施各组试验动物进行分期进行,交叉反复2次或以上。如实施2组试验动物的2个处理分3期2次的试验设计,简记为2*3交叉设计。
例:为研究新配方对奶牛产奶量的影响,设置对照饲料A1和新配方饲料A2两个处理,选择条件相近的奶牛10头,随机分为B1、B2两组,每组5头,预试期1周,实验分C1、C2两期,每期两周,按2*2交叉设计进行试验。结果如下,检验新配方饲料与对照饲料奶牛的产奶量是否存在差异?
| 时期 | C1 | C2 | |
| 处理 | A1 | A2 | |
| B1组 | B11 | 13.8 | 15.5 |
| B12 | 16.2 | 18.4 | |
| B13 | 13.5 | 16 | |
| B14 | 12.8 | 15.8 | |
| B15 | 12.5 | 14.5 | |
| 处理 | A2 | A1 | |
| B2组 | B21 | 14.3 | 13.5 |
| B22 | 20.2 | 15.4 | |
| B23 | 18.6 | 14.3 | |
| B24 | 17.5 | 15.2 | |
| B25 | 14 | 13 | |
优点:可消除个体间、试验期间的差异对实验结果的影响,提高试验精度,适合于个体差异大的动物试验;分析较为简便。
缺点:与拉丁方相比,交叉设计不能得到关于个体差异与实验时期差异大小的信息;若有重复的多因素试验相比,还不能得到因素间的交互作用,故其适用范围存在一定局限。
应用交叉设计时应注意:一是处理因素、时期、个体间不存在交互作用;二是要注意试验是否有处理残效(要设置预试期与间歇期);三是各实验组动物头数要相等。
5.正交设计
试验因素及因素水平数的增加,多因素试验的水平组合将大大增加,如3^3=27,4^4=245个水平组合,正交试验是利用正交表安排与分析多因素试验的一种设计方法。它从多因素试验的全部水平中选取部分有代表性的水平组合进行实验,通过部分分析全部,找出最优水平组合。
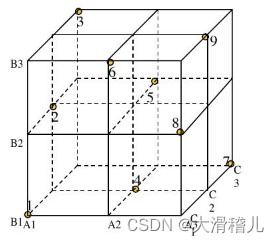
正交设计仅取其中9个点:A1B1C1,A1B2C2,A1B3C3,A2B1C2,A2B2C3,A2B3C1,A3B1C3,A3B2C1,A3B3C2
正交表的特性:一是任一列不同数字出现次数相同;二是任两列同一横行所组成的数字对出现的次数相同。
例:在矿物质对架子猪补饲实验中,考察补饲配方、用量、食盐3个因素,每个因素均有3个水平,安排一个正交实验方案。
矿物质元素补饲配方A1-A3,用量B1=15,B2=25,B3=20,食盐量C1=0,C2=4,C3=8
| 处理 | 因素 | 增重 | ||
| A | B | C | ||
| 1 | 1 | 1 | 1 | 63.4 |
| 2 | 1 | 2 | 2 | 68.9 |
| 3 | 1 | 3 | 3 | 64.9 |
| 4 | 2 | 1 | 2 | 64.3 |
| 5 | 2 | 2 | 3 | 70.2 |
| 6 | 2 | 3 | 1 | 65.8 |
| 7 | 3 | 1 | 3 | 71.4 |
| 8 | 3 | 2 | 1 | 69.5 |
| 9 | 3 | 3 | 2 | 73.7 |