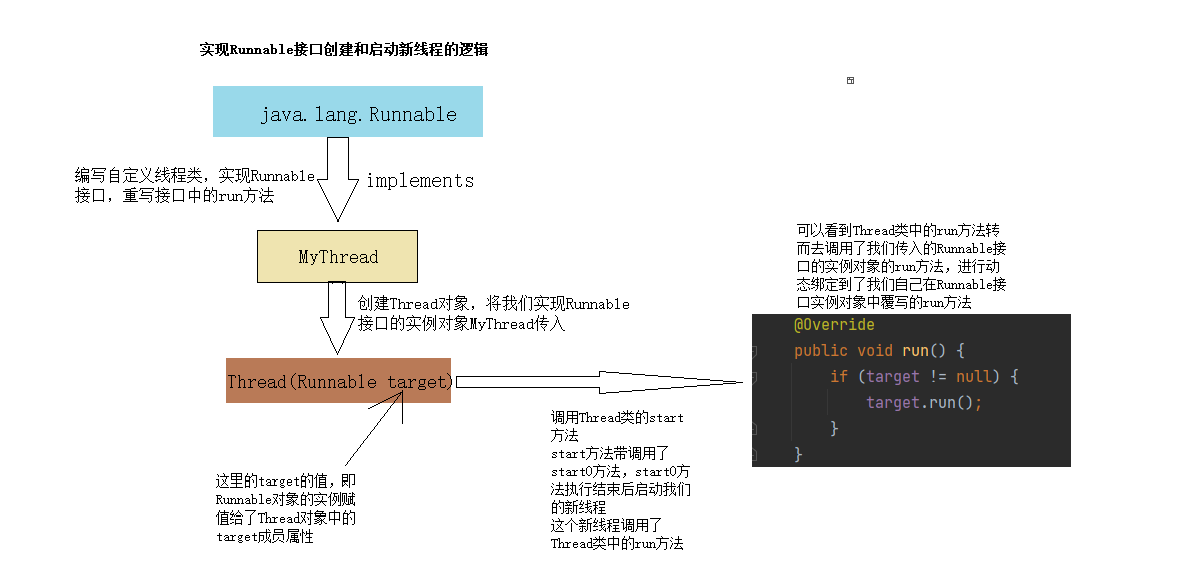
之前我们尝试使用SVM,将时序数据转为横截面的数据,使用机器学习的方法进行预测
量化择时——SVM机器学习量化择时(第1部分—因子测算):
https://blog.csdn.net/weixin_35757704/article/details/129909497
但是因为股票序列本身就是时序数据,因此在计量经济学中很早就以股票数据为例,讲解时间序列数据的分析的案例。这里我们使用LSTM,一种很常用的时间序列数据的分析模型,对股价进行预测。
文章目录
- 时间序列数据处理的特点
- LSTM量化建模
- LSTM模型介绍
- LSTM训练流程
- 特征构造
- LSTM建模代码
- 模型训练/验证效果
- 最终预测效果
时间序列数据处理的特点
时间序列的数据通常被认为是由以下几个因素构成的:
- 趋势:长期的趋势
- 季节性:存在固定且已知的周期变化趋势
- 周期性:存在不固定的周期变化趋势
- 噪声:一定的随机性
时序数据的基本假设称为“平稳时间序列假设”:
-
平稳的时间序列数据需要满足以下三个条件:
- 滑动窗口内的序列值均值为固定常数: E x t = e E_{xt} = e Ext=e
- 滑动窗口内的序列值方差为固定常数: V a r x t = v Var_{xt}=v Varxt=v
- 序列存在自相关性,协方差只与时间间隔有关: C o v ( x t , x t + k ) = c ∗ k Cov(xt,xt+k)=c*k Cov(xt,xt+k)=c∗k
其中,e,v,c都是常数;k代表时间间隔也是常数
-
非平稳的时间序列数据:与平稳相对的,统计指标会随时间变化
传统的线性模型,由于需要使用最小二乘法与最大似然估计对数据进行拟合,因此前提假设需要满足“序列平稳”,而相对于使用截面数据,机器学习的前提假设是样本点之间“独立同分布”。而对于金融数据来讲,截面因子逻辑上讲其实并不满足独立同分布,序列想要满足相对平稳的要求往往要用到周线数据+2阶差分,因此在应用层面,无法满足我们细粒度的研究,尤其是在量化应用上,交易机会瞬息万变,研究粒度越小越好。
这里我们选择LSTM(等深度学习)模型来进行建模,原因是深度学习中类似LSTM结构与激活函数等非线性变化,可以很好的突破“平稳”的前提假设,用魔法打败魔法。但与之对应的,我们需要尽可能多的构造有效性较高的数据,以提升模型的效果。
LSTM量化建模
LSTM是一种逻辑结构,就像贪吃蛇首尾相连一样,LSTM可以尝试从不同的时序变化中找到共性特征,这篇博客中不过多的介绍,主要讲解在量化中的应用场景
Pytorch LSTM参考链接:https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html
ps:有兴趣可以学习一下LSTM反向传播的计算方法,博主觉得反向传播是设计LSTM的精髓
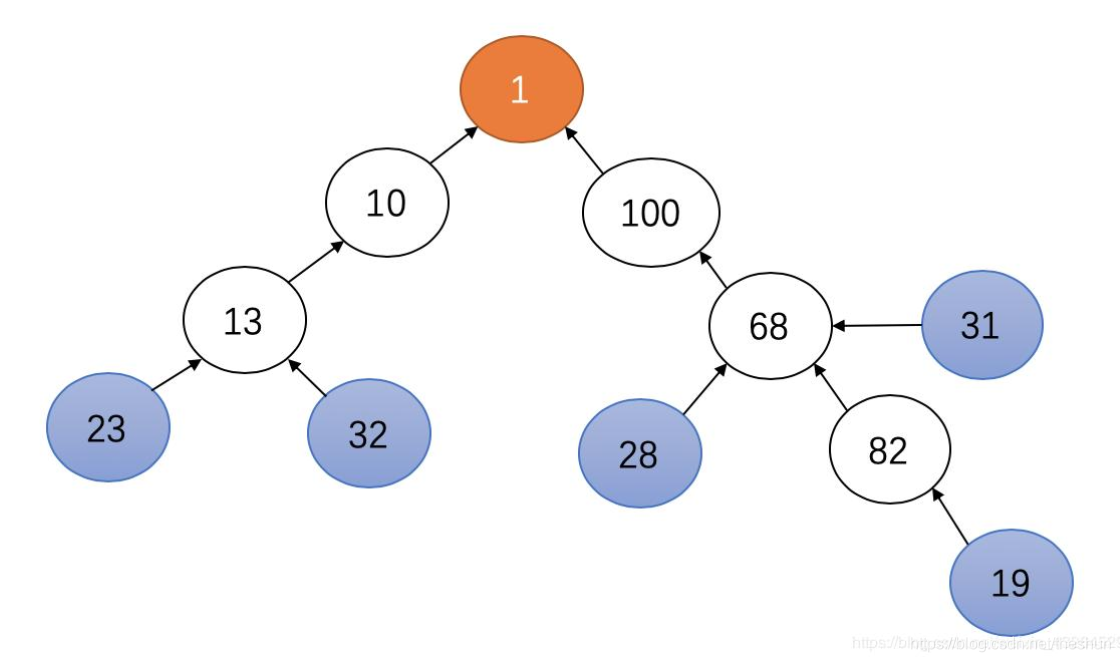
LSTM模型这篇博客就不详细介绍了,大家可以参考下面的图,这篇博客主要讲解LSTM在量化中的应用
LSTM模型介绍
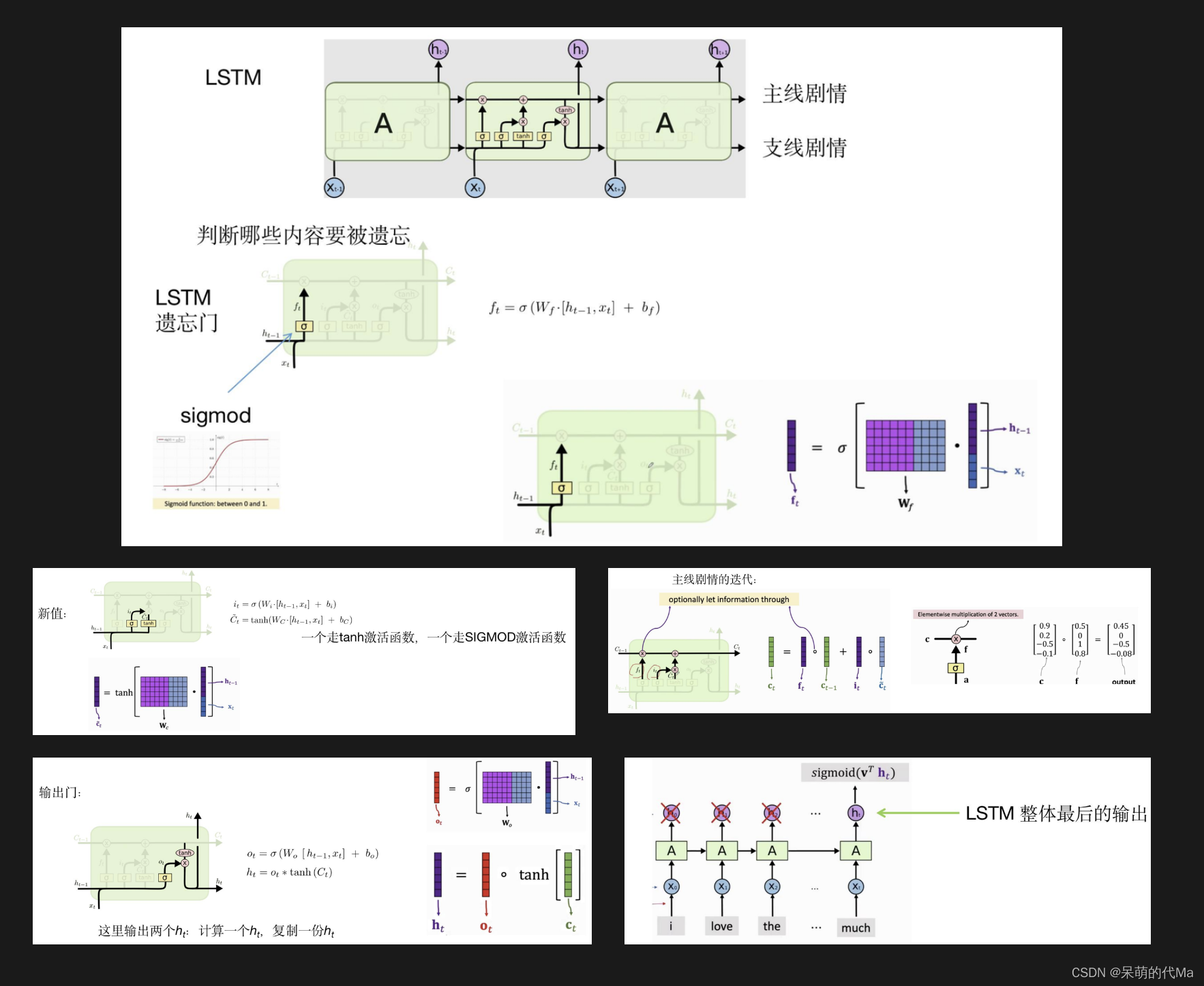
- input_size:x的特征维度
- hidden_size:隐藏层的特征维度
- num_layers:lstm隐层的层数,默认为1
LSTM训练流程
使用全部的特征进行预测,预处理流程如下:
- 对全部数据进行标准化
- 切分数据:
- 训练集:2015-2020年的后复权股票数据
- 验证集:训练集中最后的10%的数据(留一验证)
- 测试集:2020-2023年的后复权股票数据
- 优化器:Adam
- loss函数:MSE
- Batch size:64
特征构造
这里我们构造的特征简单一些,与使用SVM的特征一样:
- 过去5日换手率均值
- 过去10日换手率均值
- 过去5日涨跌幅
- 过去10日涨跌幅
- MACD指标DIF值
- MACD指标DEA值
- MACD值
- 阿隆指标(一种动量指标)DOWN值
- 阿隆指标UP值
LSTM建模代码
博主使用pytorch构造LSTM模型,模型代码如下:
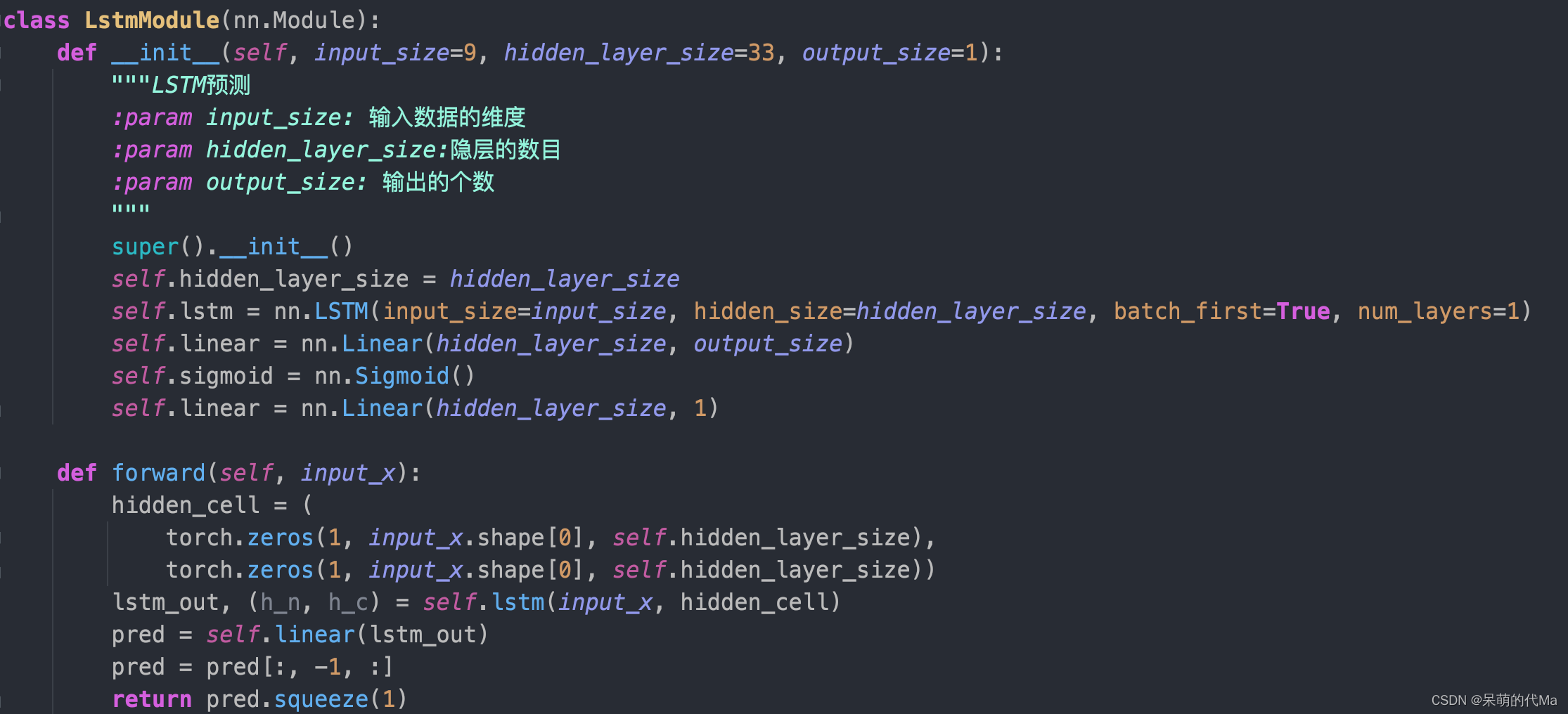
模型训练/验证效果
训练150次
其中,训练集训练效果如下图所示:
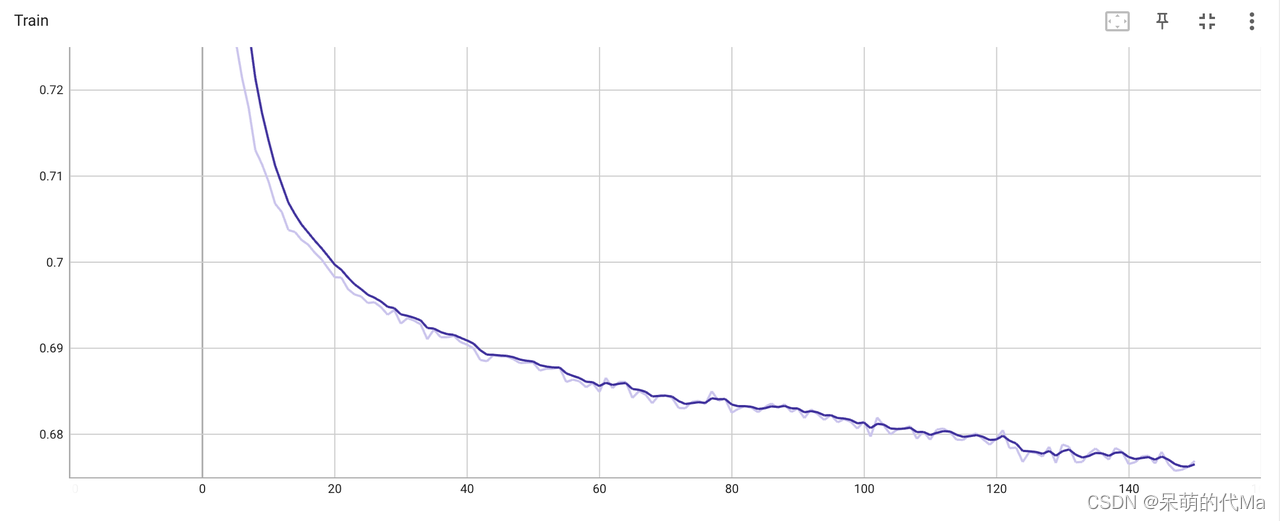
验证集的效果如下图所示:
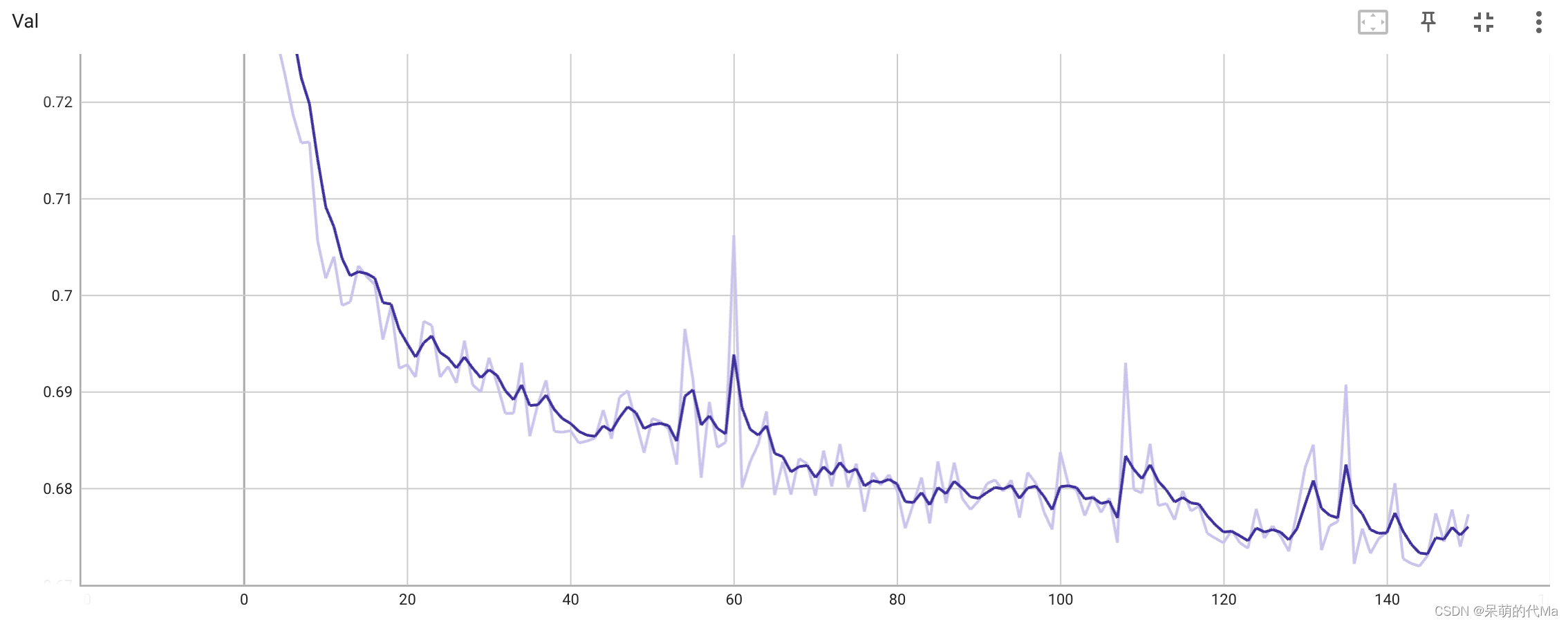
最终预测效果
预测之后,我们对测试集的结果与预测的结果分别进行等频的数据分箱,分为10个有固定数量的区间,然后绘制的胜率图效果如下:
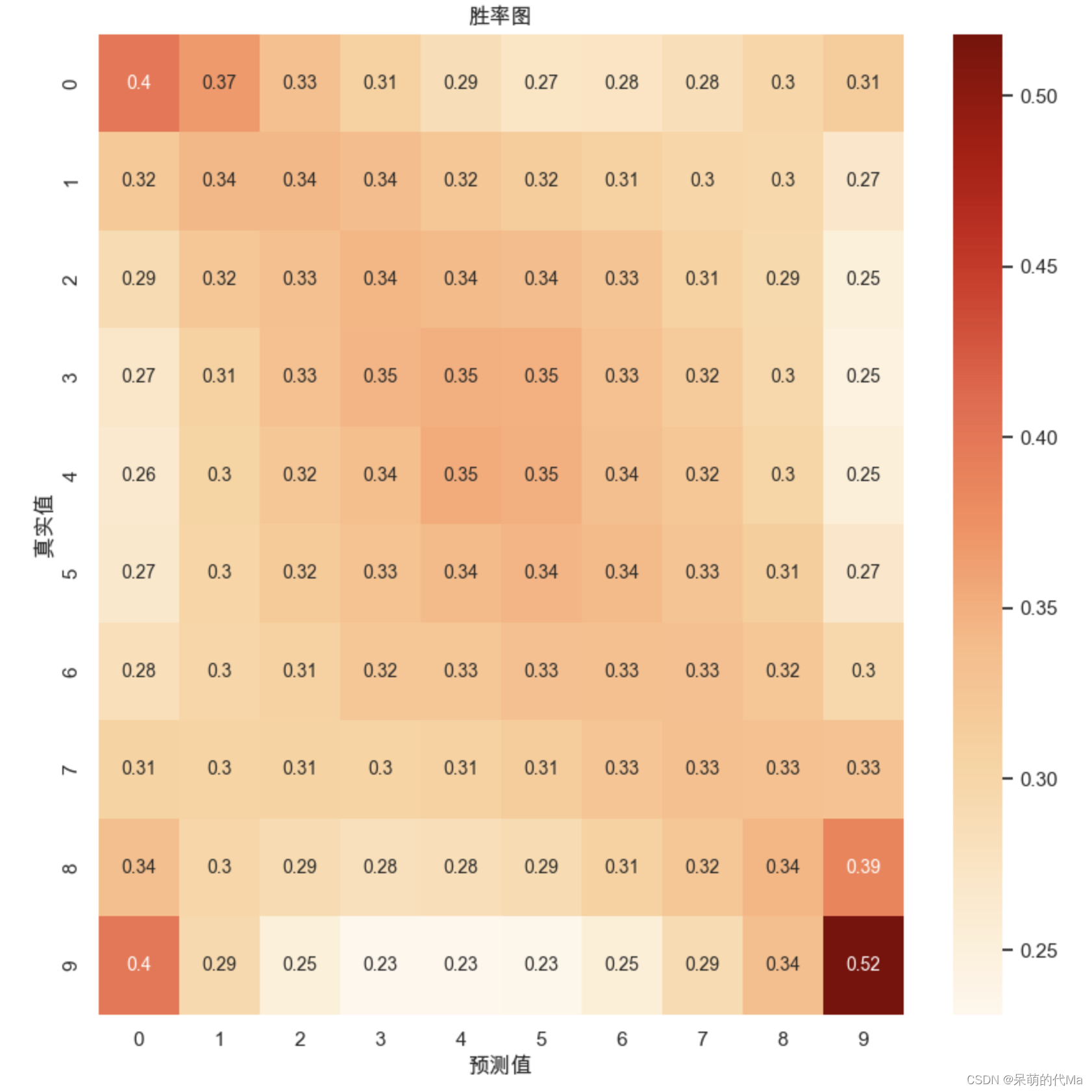
我们发现,预测效果相对较好的地方呈现“X”的形状,产生这个原因的解释是:
- 中间部分的值相对密集,比如类别4与类别5之间差距不如类别0与类别1大,因此中间区域的效果相对边缘较为集中
- 主对角线是正确的结果,而副对角线的预测相对密集,说明在模型的视角下,相同的特征走势后续上涨或下跌区分度并不明显,同样的特征后续极有可能上涨,也同样极有可能下跌
基于模型构建的策略通常会选择模型预测最高的前N%买入,即上图中最右边一列是真正会用于交易的地方,