一、PCA的目的

假设我们有一堆观测到的数据。
数据的格式是observation*feature，每一行是一个观测（也就是图里的一个点），每一列是这个数据的某个特征（即一个维度）。
假设数据矩阵是A，有m个观测和n个特征。那么我们的数据 $\in \R^{m \times n}$
举例1：每一行是一个人类，每列分别是身高、体重等等。
举例2：每一行是一个细胞，每列是某一个基因。
数据在以特征张成的空间（每个维度都是一个特征的空间）中符合某种分布。
我们可以给这个数据画一个图（假设只有两个特征）：
请添加图片描述
那么，PCA的目的就是，在空间里找到某一组正交基（一组PC），使得我们能够在更少的维度下，保留尽可能多的数据内的信息。

二、PCA的作用

大家可能或多或少听过，"PCA的作用是降维“。它降维的方法就是找到一组正交基，使得序号在前的基（也就是PC）包含更多的信息，然后选取前x个基，从而保留尽可能多信息（即损失尽可能少的信息）。
比如我们有1000张同样大小（200×200像素）的图片，那么把每张图片用一个向量表示（向量长度40000，前200个值是图片的第一行，200-400是图片的第二行，以此类推），再把每个向量/图片作为一行，每个像素点的值作为一列，就可以得到一个1000*40000的矩阵。
如果我们想把这些图片进行压缩，就可以对这个矩阵进行PCA，得到一组正交基；然后选取这些正交基的前n个，这样就得到了压缩过的1000张图片（1000×n）。
那么，PCA是如何实现的呢？实现的思路是什么？

三、PCA的思路

假设我们想把数据降维到1维。也就是把数据投影到一个方向上，使得数据在这个方向上保留的信息最多。
如何体现”信息多“？可以有两种理解方法：
① 损失的信息少，也就是所有点到这个方向上的投影距离之和最小。

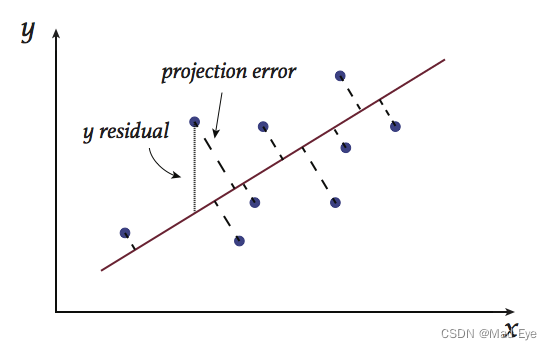
Image credit: [1]
为了使投影距离之和最小，投影到的这条线一定是过数据的中心点的（就是mean点）。
所以在做后续操作之前，我们需要把数据中心化，也就是 $A = A - m e an (A)$ 。
② 保留的信息多。也就是当每个点投影到当前维度之后，所有投影点的方差最大。
（为什么方差大就代表信息多？需要从方差的计算来思考。）
$=\frac{\sum\left(x_i-\bar{x}\right)^2}{m-1}$ ，方差正比于所有点到均值点的距离平方和。
这两种方法其实是等价的。

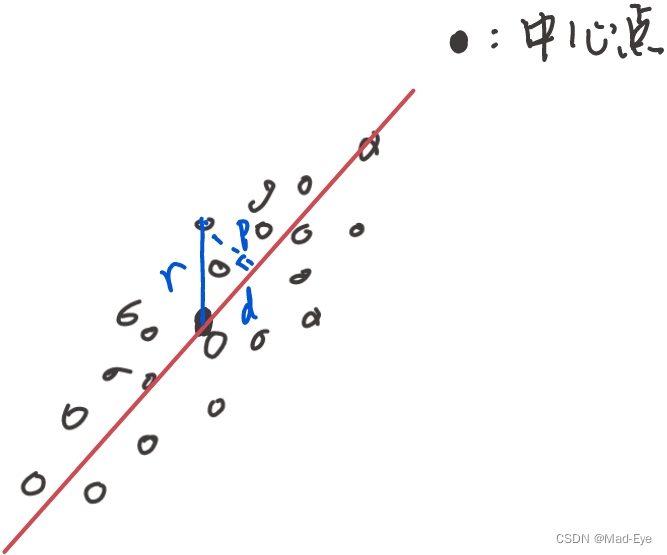
如上图，红线是投影目标向量，p是当前点的投影距离，d是投影点到中心点的距离，r是当前点到中心点的距离。
我们把投影目标向量绕中心点旋转，r不变，有： $r^2=p^2+d^2$ 。因此，最大化距离和最小化方差是在做同一个事情。
假设我们已经确定了降维到的前x维的方向，需要确定第x+1维的方向。
那么首先，我们找到的方向必须和之前的x维正交。因为如果不正交，那么两个方向向量之间是有一部分”重复信息“的，会导致新的这个方向能够引入的新信息变少。
其次，我们希望这个新方向在排除之前的维度所包含的信息之后，仍然包含最多信息的。（也就是投影距离最大，方差最小）
以此类推，找到最多n个方向。

四、PCA的实现

了解了PCA的思路之后，我们就可以考虑怎么实现了。
目前常用的实现方式有两种：①基于协方差矩阵的，和②基于特征值分解（SVD）的。
先说方法：
①基于协方差矩阵
先求出A的协方差矩阵，然后对协方差矩阵进行特征值分解，得到的特征向量和特征值就是想要的PC及其对应的variance。
②基于特征值分解
对A进行特征值分解 $A=U\Sigma V^T$ ，得到的V就包含想要的PC， $\Sigma$ 里面对应的奇异值大小就是PC的排序。

Q: 那么为什么要这样做，以及为什么基于协方差矩阵的V和基于特征值分解的V是相同的呢？
A: 把矩阵A（已经去中心化，后文提到的也都是去中心化的）投影到一个方向 $v$ ，可以表示为： $A v$ 。这就是矩阵A投影到向量v的结果。
如果我们想求投影点的方差，也就是 $\frac{\sum\left(x_i-\bar{x}\right)^2}{m-1}$ ，由于A已经去中心化， $\bar{x}=0$ 。
所以方差就是 $\frac{1}{m-1}\times \sum{x_i^2}$ ，也就是 $\frac{1}{m-1}\times ||Av||_2$ 。
$Av||_2=(Av)^T(Av)=v^TA^TAv$ 。
因此，我们想要找到一个方向 $v$ ，使得 $v^T A^TAv$ 最大。
设 $v^TA^TAv=\lambda$ ，那么有 $A^TAv=\lambda v$ ，即 $v$ 是 $A^TA$ 的特征向量。
所以，问题就变成了：试图找到使得 $A^TA$ 的特征值最大的特征向量！
①当A是中心化的矩阵时，A的协方差矩阵为 $\frac{A^TA}{m-1}$ ，基于谱定理[2]。所以对协方差矩阵进行特征值分解就可以得PC。
②基于SVD， $A=U\Sigma V^T,A^TA=V \Sigma^2 V^T$ 。由于 $V$ 是正交矩阵，有 $V^T=V^{-1}$ ，所以 $V$ 就是对 $A^TA$ 进行特征值分解得到的特征向量矩阵。