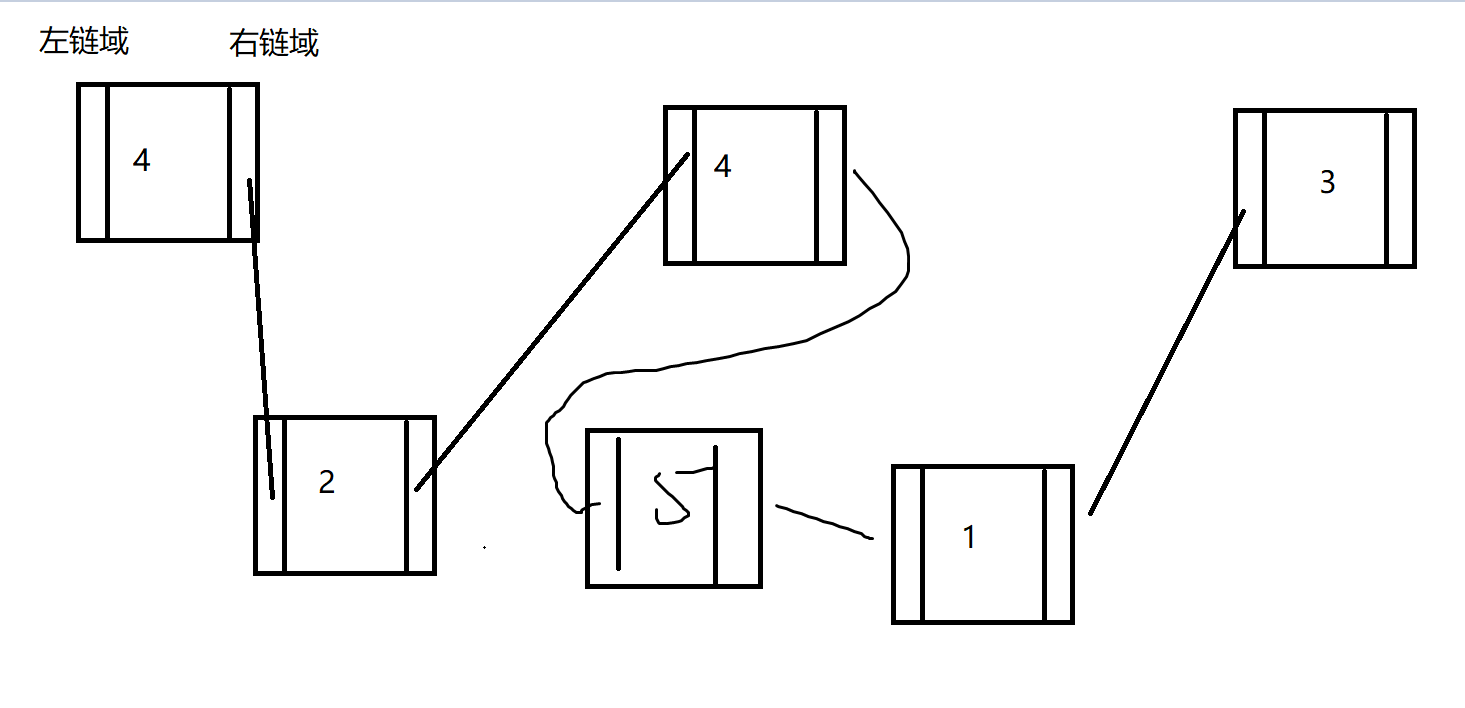
t检验能用来进行两个处理平均数之间的假设检验,但一般研究会出现多个处理优劣的比较,即需要进行多个处理平均数的假设检验,此时t检验不再适用,具体表现在检验量增加,如k个处理,要进行k*(k-1)/2次检验;未充分利用试验资料所提供的全部信息使得误差估计的精确性降低,从而降低了灵敏度;推断的可靠性降低,未比较两个平均数秩次问题,检验的Ⅰ型错误率大。
【无效假设指的是数据间差异不显著,备择假设则认为其显著。】
【Ⅰ型错误指的是把原本正确的无效假设否定了,即为:弃真;Ⅱ型错误与之相反,无效假设错误,备择假设正确,但认可了无效假设,即为:纳伪。】
【对于Ⅰ型错误,我们基于小概率事件实际不可能发生来确定无效假设是否被否定,但实际而言,小概率不事件并非决定不可能发生事件,但犯该错误的概率不大于显著水平α(SAS中记为:alpha)】
【对于Ⅱ型错误,一般与显著水平α成反比,样本含量成反比,原总体标准差成正比】
【若一个试验耗费大可靠性要求高,事关重大(如药物毒性检验)、不允许反复,则显著水平α值要取小,对试验条件难控制,误差较大的,可将显著水平α放宽到0.1-0.25】
SAS的方差分析一般含7种类型:一是单因素试验各处理重复数相等资料方差分析;二是单因素试验各处理重复数不等资料方差分析;三是两因素交差分组单独观察值资料的方差分析;四是两因素交差分组重复观察值试验资料的方差分析;五是两因素系统分组次级样本含量相等资料方差分析;六是两因素系统分组次级样本含量不等资料方差分析;七是正反弦转换后的资料进行方差分析。
【编程口诀:长短一致用anova,长短不一用glm,交叉分组有重复,model不忘a*b】
1.单因素试验各处理重复数相等资料方差分析
例:对比4种配合饲料对鱼的喂养效果,选取了条件基本相同的鱼20尾,随机分4组,每组投喂不同饲料,经一个月的试验,比较配合饲料的优劣。
| 饲料种类 | 增重 | ||||
| A1 | 31.9 | 27.9 | 31.8 | 28.4 | 35.9 |
| A2 | 24.8 | 25.7 | 26.8 | 27.9 | 26.2 |
| A3 | 22.1 | 23.6 | 27.3 | 24.9 | 25.8 |
| A4 | 27 | 30.8 | 29 | 24.5 | 28.5 |
Data fish;
Input x y@@;
Cards;
1 31.9 1 27.9 1 31.8 1 28.4 1 35.9
2 24.8 2 25.7 2 26.8 2 27.9 2 26.2
3 22.1 3 23.6 3 27.3 3 24.9 3 25.8
4 27.0 4 30.8 4 29.0 4 24.5 4 28.5
;
Proc anova ;
Class x;
Model y=x;
Means x/LSD duncan SNK;
Means x/LSD DUNC N SNK alpha =0.01;
Run;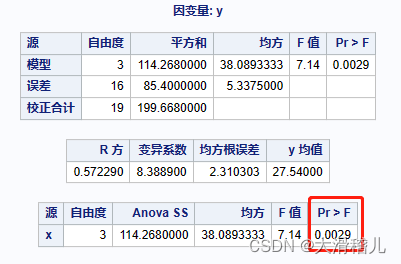
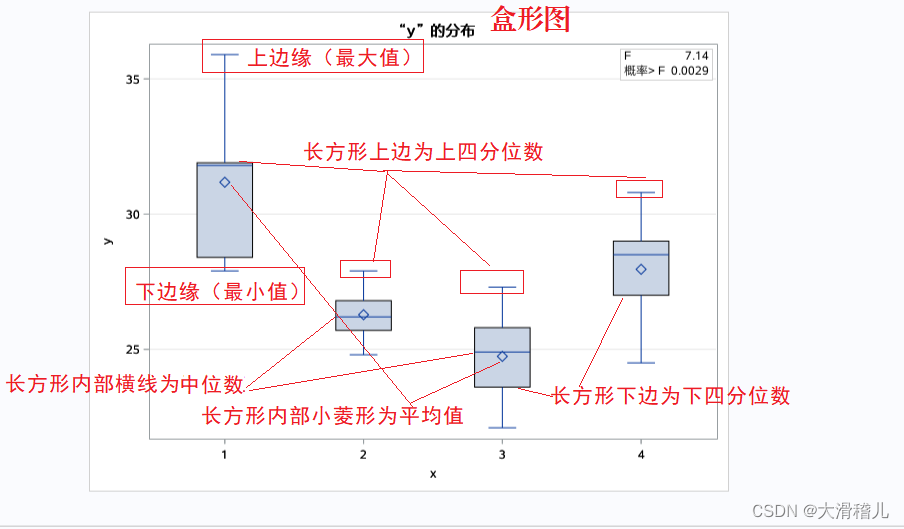
答:不同配合饲料差异极其显著【各处理平均数间差异极显著,或简述为“F值极显著”】,其中效果比较为1>4>2>3。
2.单因素试验各处理重复数不等资料方差分析
例:5个不同品种猪的育肥试验,后期30d增重(kg)如表。检验品种间增重有无差异。
| 品种 | 增重kg | |||||
| B1 | 21.5 | 19.5 | 20 | 22 | 18 | 20 |
| B2 | 16 | 18.5 | 17 | 15.5 | 20 | 16 |
| B3 | 19 | 17.5 | 20 | 18 | 17 | |
| B4 | 21 | 18.5 | 19 | 20 | ||
| B5 | 15.5 | 18 | 17 | 16 | ||
data sow;
input breed y@@;
cards;
1 21.5 1 19.5 1 20 1 22 1 18 1 20
2 16 2 18.5 2 17 2 15.5 2 20 2 16
3 19 3 17.5 3 20 3 18 3 17
4 21 4 18.5 4 19 4 20
5 15.5 5 18 5 17 5 16
;
proc GLM;
class breed;
model y=breed;
means breed/Duncan;
means breed/Duncan alpha=0.01;
run;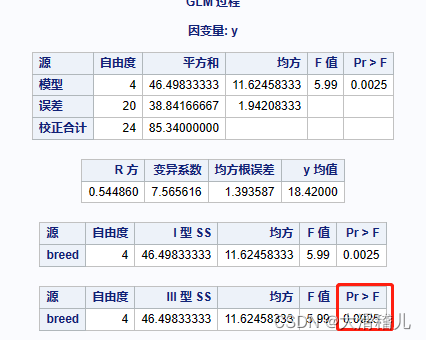
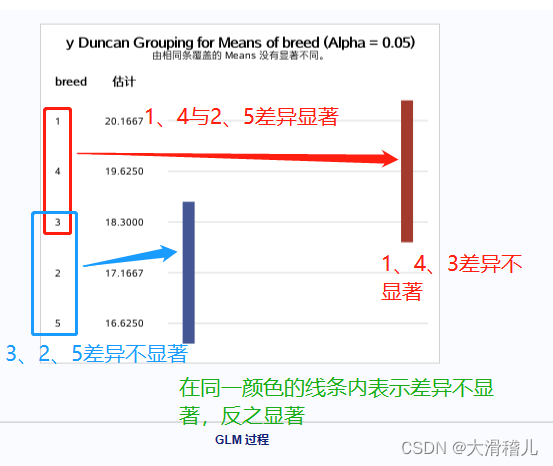
答:检验品种间增重差异极显著。