一、前言

二、整数规划模型

1、整数规划特征

2、分枝定界法

①分枝定界法的步骤

②实际解题

三、0-1整数规划

1、隐枚举法

①隐枚举法的步骤：

②案例

2、匈牙利法

①指派问题

②匈牙利法步骤

③案例

一、前言

我们先来看一个例子：

书接上回，伍老师想要给新买的公寓刷油漆，四面墙一共有200平方米，伍老师和男友商量了一下，想涂成粉色的，因为伍老师的男友高大威猛，而粉色又是猛男的颜色。于是，第二天去宜家装饰广场看了一下油漆的价格。市面上流行的油漆一共有三种：

A类：旺旺牛仔牌油漆，一桶大概2L，能涂完7平方米，价格在50元/桶

B类：螺蛳粉牌油漆，一桶大概5L，能涂完20平方米，价格在130块/桶

C类：麻辣王子牌油漆，一桶大概8L，能涂完35平方米，价格在300元/桶

已知伍老师希望预算最少，伍老师的宝马后备箱还有48L的存储空间，伍老师的男朋友小李很想向女朋友展现自己的才华，凭借一己之力，算出三种牌子的油漆，分别要买多少桶。那么，大家能不能给四肢发达，头脑简单的伍老师的男朋友出个主意呢？相信大家的智慧能让伍老师觉得自己的男朋友，真是一个持家的人！

读者们呵呵一笑，大师我悟了，这不就是线性规划吗，直接用MATLAB一求解，真简单，代码我都知道怎么写：

    c=[50 140 300];
    A=[2  5  8;-7 -20 -35];
    b=[48 ; -200];
    Aeq=[];
    beq=[];
    vlb=[0,0,0];
    vub=[];             
    [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

结果为：

这个答案对吗？漏漏漏！螺蛳粉和麻辣王子牌子的油漆虽好，但是有谁见过买三分之一桶油漆的？就算是食物，也不可能只买半包麻辣王子，半碗螺蛳粉吧？所以，今天我们的任务之一就是：限制X的条件为整数，求出线性规划的可行解。

二、整数规划模型

1、整数规划特征

一个规划问题中要求部分或全部决策变量是整数，则这个规划称为整数规划。

当要求全部变量（包括松弛变量、剩余变量）取整数值的，称为纯整数规划；只要求一部分变量取整数值的，称为混合整数规划；所有决策变量非0即1的，称为0-1整数规划。如果模型是线性的，称为整数线性规划。

常见的整数规划问题的求解算法有以下几种：

A.分枝定界法：可求纯或混合整数线性规划

B.割平面法：可求纯或混合整数线性规划

C.隐枚举法：用于求解0-1整数规划

D.匈牙利法：解决指派问题（0-1规划特殊情形）

E.蒙特卡罗法：求解各种类型规划

有很多种整数规划的案例，例如：

1. 变量是人数、机器设备台数或产品件数等都要求是整数，总不能把人劈成两半吧，那样想想就瘆得慌。

2. 对某一个项目要不要投资的决策问题，可选用一个逻辑变量 x，当x=1表示投资，x=0表示不投资；

3. 人员的合理安排问题，当变量xij=1表示安排第i人去做j工作，xij=0表示不安排第i人去做j工作。逻辑变量也是只允许取整数值的一类变量。

2、分枝定界法

①分枝定界法的步骤

1. 求整数规划的松弛问题最优解；

2. 若松弛问题的最优解满足整数要求，得到整数规划的最优解，否则转下一步；

3.任意选一个非整数解的变量xi，在松弛问题中加上约束 xi≤[xi]及xi≥[xi]+1组成两个新的松弛问题，称为分枝。新的松弛问题具有特征：当原问题是求最大值时，目标值是分枝问题的上界；当原问题是求最小值时，目标值是分枝问题的下界；

4. 检查所有分枝的解及目标函数值，若某分枝的解是整数并且目标函数值大于（max）等于其它分枝的目标值，则将其它分枝剪去不再计算,若还存在非整数解并且目标值大于（max）整数解的目标值，需要继续分枝，再检查，直到得到最优解。

②实际解题

我们按照刚刚的那个题为例，若使用分枝定界法，，初始的线性规划模型为：

$min Z=50x_{1}+130x_{2}+300x_{3}$

$s.t. \, \, \, \: \begin{matrix} 2x_{1}+5x_{2}+8x_{3}\leq 48\\ 7x_{1}+20x_{2}+35x_{3}\geq 200\\ x_{j}\geq 0,x_{j}\, \, is\, \, integer \end{matrix}$

那么，先不管它是不是一个整数规划，我们按照线性规划模型解题，则初始解为x=（0,5.334,2.667），选择x2并加上约束条件x2<=5与x2>=6，得到两组线性规划如下：

A.x2<=5

$min Z=50x_{1}+130x_{2}+300x_{3}$

$s.t. \, \, \, \: \begin{matrix} 2x_{1}+5x_{2}+8x_{3}\leq 48\\ 7x_{1}+20x_{2}+35x_{3}\geq 200\\ x_{2}\leq 5\\x_{j}\geq 0,x_{j}\, \, is\, \, integer \end{matrix}$

B.x2>=6

$min Z=50x_{1}+130x_{2}+300x_{3}$

$s.t. \, \, \, \: \begin{matrix} 2x_{1}+5x_{2}+8x_{3}\leq 48\\ 7x_{1}+20x_{2}+35x_{3}\geq 200\\ x_{2}\geq 6\\x_{j}\geq 0,x_{j}\, \, is\, \, integer \end{matrix}$

A与B分道扬镳了，这也就是为什么要叫做分支定界的原因，紧接着求接出A与B的线性规划问题的解，并且判断是不是整数解就行了。但是很可惜的是，小编的题目数据没编好，A与B均是无整数解的，小李也要哭晕在厕所，并且喃喃的说道：我太难了。看来小李要用自己的三寸不烂之舌劝说老板卖自己三分之一桶油漆了。

三、0-1整数规划

1、隐枚举法

对于n个决策变量，反正取值只有0和1，我都列出来，再一个一个排除，也用不了太多时间。但是，之所以叫“隐”枚举法，是因为它不单单是枚举，还有额外的步骤来限制它。

①隐枚举法的步骤：

1.找出任意一可行解，目标函数值为Z0

2. 原问题求最大值时，则增加一个约束

c1x1 + c2 x2 +……+ cn xn $\leq$ Z0 (*)

当求最小值时，上式改为小于等于约束

3. 列出所有可能解，对每个可能解先检验式（*），若满足再检验其它约束，若不满足式（*），则认为不可行，若所有约束都满足，则认为此解是可行解，求出目标值

4. 目标函数值最大（最小）的解就是最优解

②案例

小李自掏腰包买完油漆后，伍老师要开始粉刷墙壁了。已知有下面这几位工人：

a.小李，伍老师的男朋友，可以替伍老师免费打工，但是效率很慢，而且还很不专业，一个上午可以刷20平方米

b.光头哥，伍老师下班路上遇到的粉刷匠，工资175，一个上午可以涂80平方米

c.老莫，伍老师的热心邻居，爱好吃鱼，与伍老师很熟，工资80，一个上午可以涂40平方米

d.昊仔，宜家装饰广场的粉刷扛把子，工资220，但是一个上午可以涂100平方米

e.肖阿姨，粉刷解的卷王，工资150，一个上午可以涂75平方米

已知伍老师希望在上午一个小时内粉刷完墙壁，并且希望所花的钱最少，那么伍老师该选哪些人呢？

我们先令 $x_{j},j=1,2,3,4,5$ 代表是否选择小李、光头哥、老莫、昊仔以及肖阿姨，那么xj只可能为0或者1，并且满足方程 $20x_{1}+80x_{2}+40x_{3}+100x_{4}+75x_{5}\geq 200$ （式子a），我们期望付的钱最少，即min z= $175x_{2}+80x_{3}+220x_{4}+150x_{5}\leq 405$ 。我们先找一个满足方程的解，如（1,1,1,0,1），需要支付405元，所以我们增设条件 $175x_{2}+80x_{3}+220x_{4}+150x_{5}\leq 405$ （式子b），当用枚举法判断这一组解是否满足式子b后，再判断是否满足式子a。

X	满足式子a？	满足式子b？	z	X	满足式子a？	满足式子b？	z
(0,0,0,0,0)	是	否		(1,0,0,0,0)	是	否
(0,0,0,0,1)	是	否		(1,0,0,0,1)	是	否
(0,0,0,1,0)	是	否		(1,0,0,1,0)	是	否
(0,0,0,1,1)	否			(1,0,0,1,1)	否	否
(0,0,1,0,0)	是	否		(1,0,1,0,0)	是	否
(0,0,1,0,1)	是	否		(1,0,1,0,1)	是	否
(0,0,1,1,0)	是	否		(1,0,1,1,0)	是	否
(0,0,1,1,1)	否			(1,0,1,1,1)	否
(0,1,0,0,0)	是	否		(1,1,0,0,0)	是	否
(0,1,0,0,1)	是	否		(1,1,0,0,1)	是	否
(0,1,0,1,0)	否			(1,1,0,1,0)	否
(0,1,0,1,1)	否			(1,1,0,1,1)	否
(0,1,1,0,0)	是	否		(1,1,1,0,0)	是	否
(0,1,1,0,1)	是	否		(1,1,1,0,1)	是	是	405
(0,1,1,1,0)	否			(1,1,1,1,0)	否
(0,1,1,1,1)	否			(1,1,1,1,1)	否

综上所述，只有（1,1,1,0,1）满足，开局即王炸，我们一开始就猜对了，需要小李、光头哥、老莫以及肖阿姨参加工作，昊仔直接失业了。

2、匈牙利法

①指派问题

指派问题的数学模型的标准形式：

设n 个人被分配去做n 件工作，规定每个人只做一件工作，每件工作只有一个人去做。已知第i个人去做第j 件工作的效率（时间、费用或者其他代价）为Cij(i=1.2…n;j=1.2…n)并假设Cij ≥0。问应如何分配才能使总效率（时间或费用）最高？

其决策变量为：

指派问题的数学模型为：

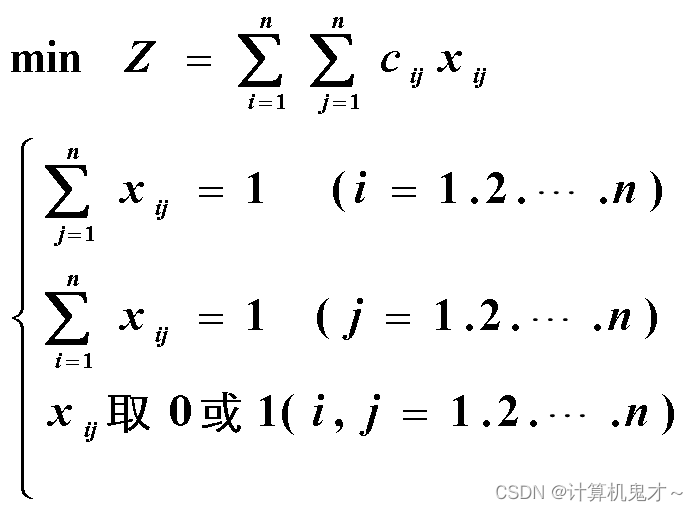
②匈牙利法步骤

解决指派问题我们要用到一个定理，叫做松尼格定理：如果从分配问题效率矩阵[aij]的每一行元素中分别减去(或加上)一个常数ui，从每一列中分别减去(或加上)一个常数vj，得到一个新的效率矩阵[bij]，则以[bij]为效率矩阵的分配问题与以[aij]为效率矩阵的分配问题具有相同的最优解。

那么解题步骤为：

1) 变换指派问题的系数矩阵(cij)为(bij)，使在(bij)的各行各列中都出现0元素，即从(cij)的每行元素都减去该行的最小元素；再从所得新系数矩阵的每列元素中减去该列的最小元素。

2) 进行试指派，以寻求最优解。在(bij)中找尽可能多的独立0元素，若能找出n个独立0元素，就以这n个独立0元素对应解矩阵(xij)中的元素为1，其余为0，这就得到最优解。

找独立0元素，常用的步骤为：

1. 从只有一个0元素的行开始，给该行中的0元素加圈，记作 $\circledcirc$ 。然后划去 $\circledcirc$ 所在列的其它0元素，记作Ø ；这表示该列所代表的任务已指派完，不必再考虑别人了。依次进行到最后一行。

2.从只有一个0元素的列开始（画Ø的不计在内），给该列中的0元素加圈，记作 $\circledcirc$ ；然后划去 $\circledcirc$ 所在行的0元素，记作Ø ，表示此人已有任务，不再为其指派其他任务了。依次进行到最后一列。

3.若仍有没有划圈的0元素，且同行(列)的0元素至少有两个，比较这行各0元素所在列中0元素的数目，选择0元素少这个0元素加圈(表示选择性多的要“礼让”选择性少的)。然后划掉同行同列的其它0元素。可反复进行，直到所有0元素都已圈出和划掉为止。

4.若 $\circledcirc$ 元素的数目m 等于矩阵的阶数n（即：m＝n），那么这指派问题的最优解已得到。若m < n, 则转入下一步。

3) 用最少的直线通过所有0元素。其方法：

a.对没有 $\circledcirc$ 的行打“√”；

b.对已打“√” 的行中所有含Ø元素的列打“√” ；

c.再对打有“√”的列中含 $\circledcirc$ 元素的行打“√” ；

d.重复a、b两步直到得不出新的打√号的行、列为止；

e. 对没有打√号的行画横线，有打√号的列画纵线，这就得到覆盖所有0元素的最少直线数。

4) 变换矩阵(bij)以增加0元素在没有被直线通过的所有元素中找出最小值，没有被直线通过的所有元素减去这个最小元素；直线交点处的元素加上这个最小值。新系数矩阵的最优解和原问题仍相同。转回第2步。

③案例

伍老师房子的装修第一天很顺利，但还需完成安装玻璃、贴瓷砖、装马桶还有做晚饭四件事情，分别记作A、B、C、D。现有伍老师、小李、老莫、洋洋四人空闲，他们完成这四件事情所需时间如下表所示，问如何分派任务，可使总时间最少？（单位：分钟）

安装玻璃贴瓷砖装马桶做晚饭
伍老师 60 70 110 20
小李 40 50 90 80
老莫 30 10 100 40
洋洋 50 90 80 20

第一步：变换系数矩阵，增加0元素

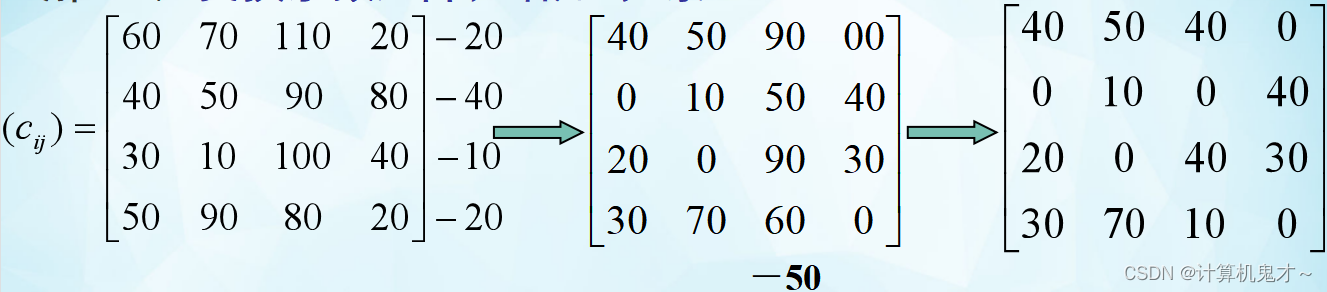
第二步：试指派（找独立0元素）

我们可以得到如下的矩阵：

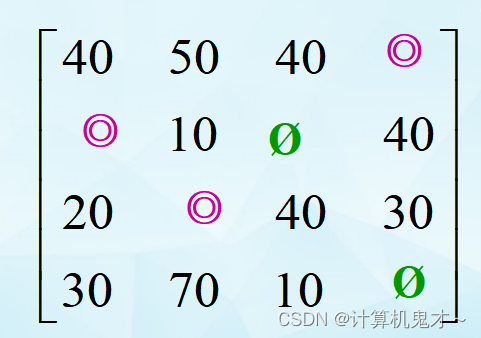
3）作最少的直线覆盖所有0元素

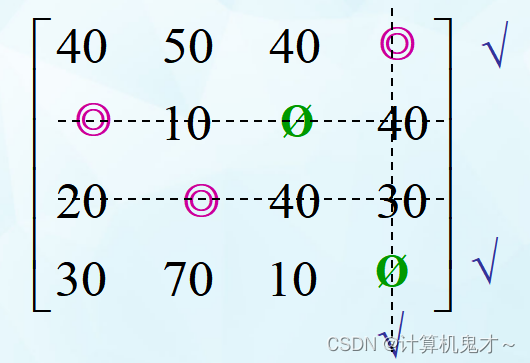
4）没有被直线通过的元素中选择最小值为10，变换系数矩阵，将没有被直线通过的所有元素减去这个最小元素；直线交点处的元素加上这个最小值。得到新的矩阵，重复2）步进行试指派，得到4个独立零元素，所以最优解矩阵为： $\begin{pmatrix} & & & 1\\ 1& & & \\ & 1 & & \\ & & 1 & \end{pmatrix}$ ，最少时间为40+10+80+20=150min，即小李安装玻璃，老莫贴瓷砖，洋洋装马桶，伍老师给大家伙做完饭吃！