目录

一、二叉树的完全性检验

 二、前序遍历的非递归写法

三、中序遍历的非递归写法

四、后序遍历的非递归写法

---

一、二叉树的完全性检验

给定一个二叉树的 root ，确定它是否是一个 完全二叉树 。 在一个 完全二叉树 中，除了最后一个关卡外，所有关卡都是完全被填满的，并且最后一个关卡中的所有节点都是尽可能靠左的。它可以包含 1 到 2h 节点之间的最后一级 h 。

 

这道题目需要分阶段：将一颗完全二叉树看做两个阶段。

阶段一：此时的节点都是度为2的结点，当碰到第一个只有左子树没有右子树或者叶子结点，从该结点之后的结点应该都在二叉树。

阶段二：此时的节点全都是叶子结点，碰到一个反例直接return false。

当遇到一个结点只有右子树，那么直接return false。

所以首先判断树是否只有一个结点，root.left ==null&&root.right==null如果满足这个条件那么直接返回true。

主要就是根据层序遍历入队出队进行判断是否是完全二叉树，所以首先创建一个对列deque，将根节点入队，然后设置一个两边isSecondStep来判断是否在第二阶段。

然后进行出队并且将出队元素存储起来，然后进行判断现在是哪个阶段，这时是第一阶段，若左右子树都不为空，那么就让他们的左右子树入队即可。

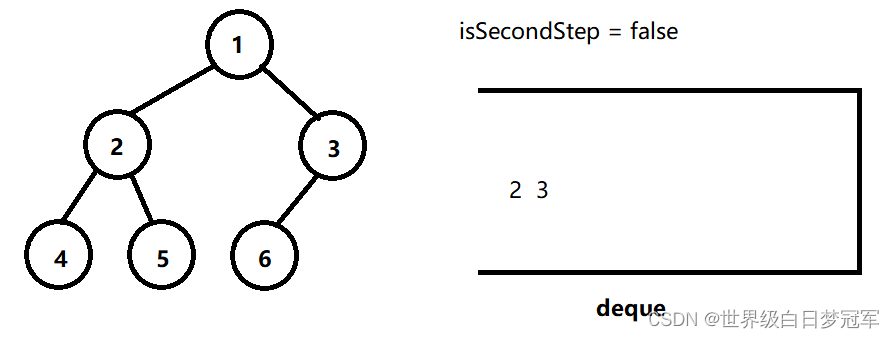
 然后继续出队，这时还是第一阶段，左右子树都不为空，让他们的左右子树入队。

 然后继续出队，这时还是第一阶段，但是这个时候左子树不为空右子树为空，所以进入第二阶段设置isSecondStep为true，然后将左子树入队。

 这时在进入循环就是第二阶段了，判断每个出队元素的左右子树是否都为空，若不是那么立即返回false。进行到最后了就返回isSecondStep即可。

    public boolean isCompleteTree(TreeNode root) {
        if(root.left ==null&&root.right==null){
            return true;
        }
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        boolean isSecondStep = false; 
        while(!deque.isEmpty()){
            TreeNode tmp = deque.poll();
            if(!isSecondStep) {
                if (tmp.right != null && tmp.left != null) {
                    deque.offer(tmp.left);
                    deque.offer(tmp.right);
                } else if (tmp.right != null && tmp.left == null) {
                    return false;
                } else if (tmp.left != null) {
                    isSecondStep = true;
                    deque.offer(tmp.left);
                }else{
                    isSecondStep = true; 
                }
            }else{
                if(tmp.left!=null||tmp.right!=null){
                    return false;
                }
            }
        }
        return isSecondStep;
    }

 二、前序遍历的非递归写法

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

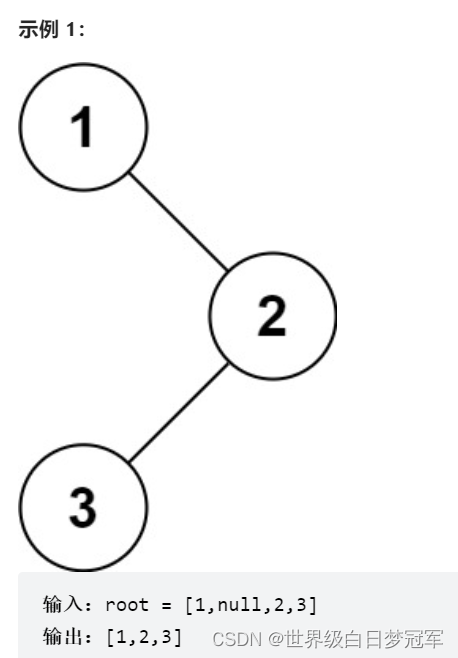
 所有的深度优先遍历都需要借助栈结构进行非递归写法。

 不断地碰到根节点入栈以后，出栈，然后先将右子树入栈，再将左子树入栈中（保证左子树在右子树上方优先出栈），达到根左右的遍历目的。

首先排除树为空的情况，然后创建栈存储根节点。

 然后进入循环，循环的终止条件就是栈空，出栈取出根节点，当该节点的右子树不为空那么就入栈，然后再判断左子树是否为空，为空则直接忽略。

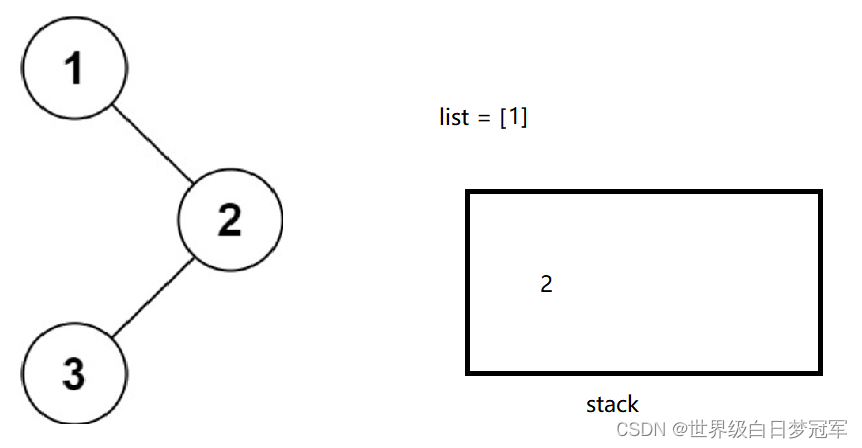
 然后继续出栈取出根节点，这时右子树为空那么久忽略，然后左子树非空，非将左子树入栈。

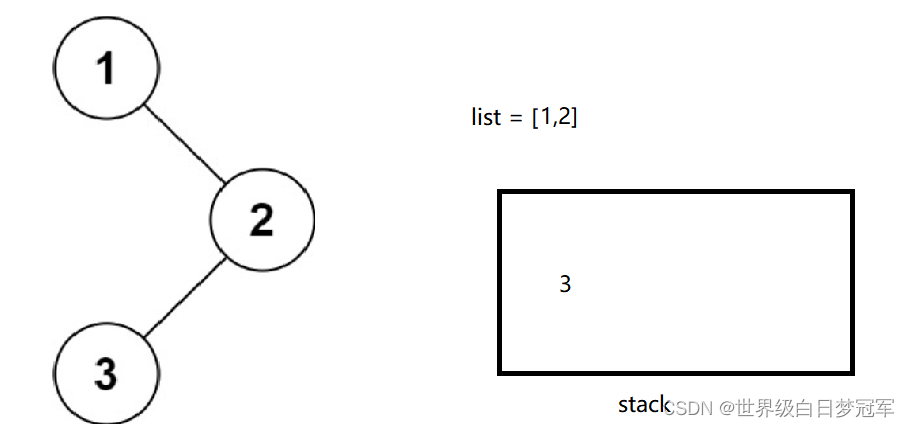
 然后再出栈，这时左右子树都为空则忽略，并且stack为空所以循环结束，返回list即可。

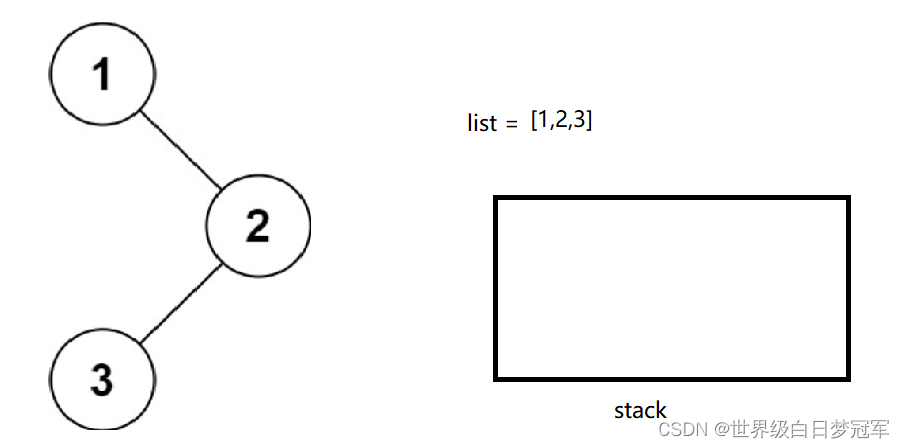
    public List<Integer> preorderTraversal(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> stack  = new ArrayDeque<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.poll();
            list.add(node.val);
            if(node.right!=null){
                stack.push(node.right);
            }
            if(node.left!=null){
                stack.push(node.left);
            }
        }
        return list;
    }

三、中序遍历的非递归写法

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

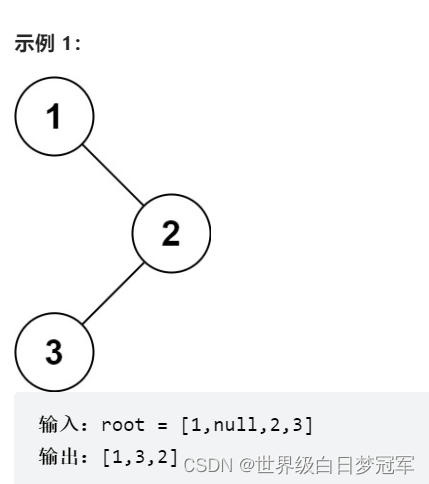
 中序遍历是左跟右的顺序，所以需要先将向左碰到的节点压入栈中，直到碰到第一个左子树为空的结点这时就可以输出了。

所以首先排除树为空的情况，然后创建一个变量node使他等于树根，然后进入循环，若node！=null那么将他入栈，然后让node = node.left，向左搜索。

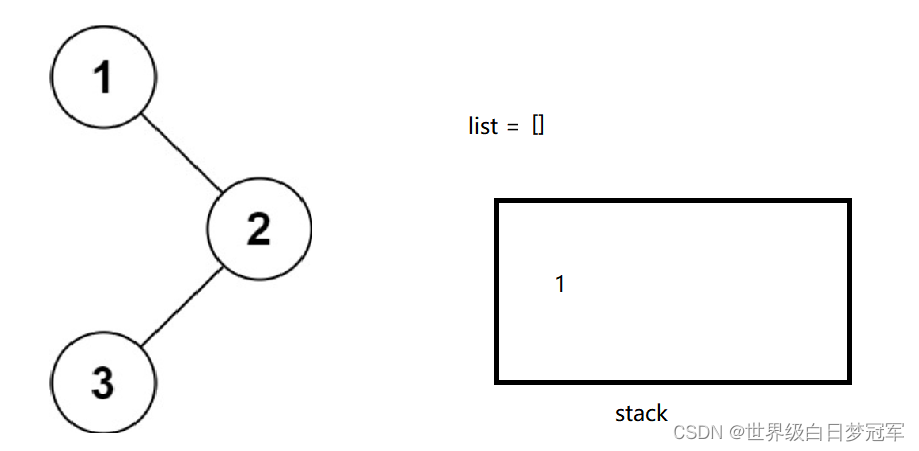
 这时node就等于空了。所以找到了最左的结点，保存并且出栈，然后去探索它的右节点。

 再次进入循环仍然一直向左探索，并且入栈。

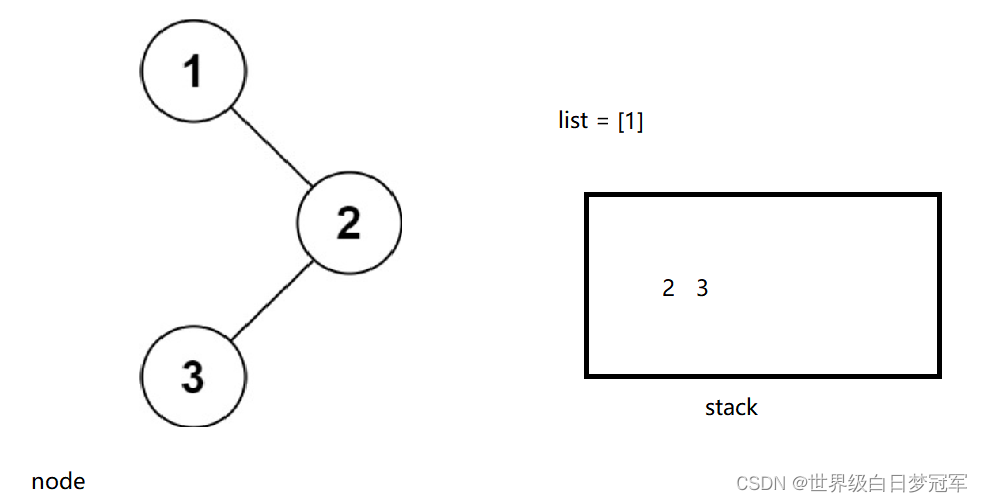
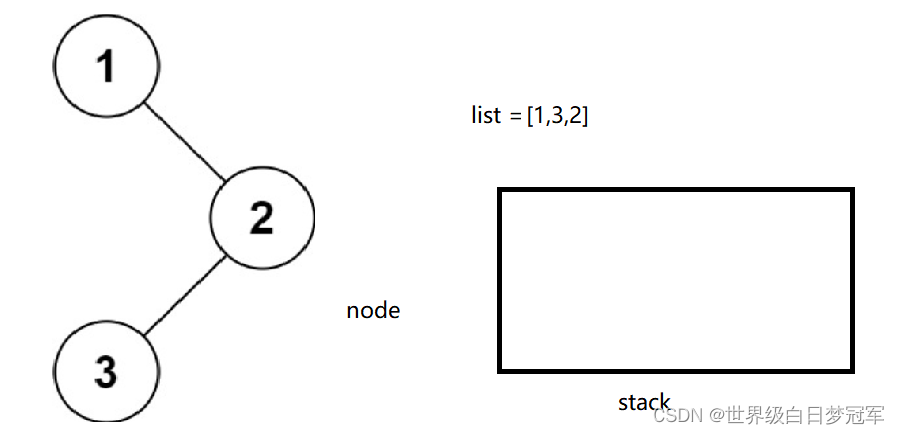
 这时node就等于空了，保存并且出栈，继续探索其右节点，但是这时它的右节点是空的，所以循环的条件是node !=null ||!stack.isEmpty()，需要继续进入循环。

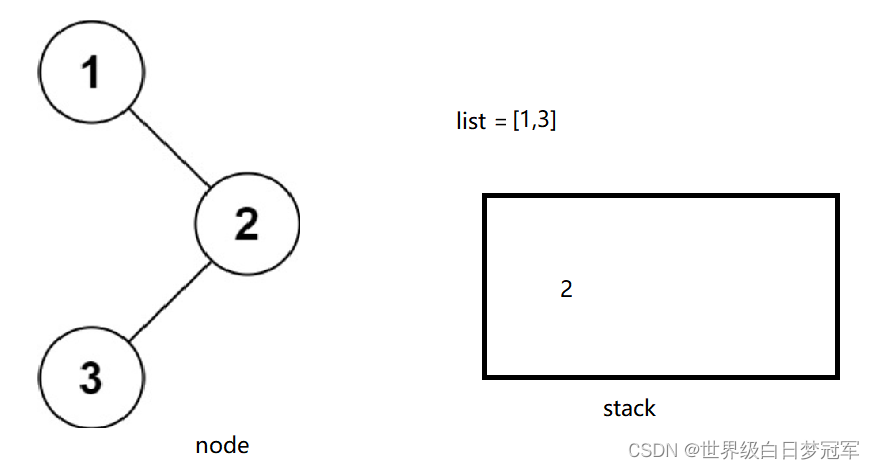
 这时node为空，所以直接出栈，然后探索出栈元素的右节点，但是这时右节点为空并且栈为空，所以循环结束。

    public List<Integer> inorderTraversal(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> stack  = new ArrayDeque<>();
        TreeNode node = root;
        while (node !=null ||!stack.isEmpty()){
            while(node!=null){
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            list.add(node.val);
            node = node.right;
        }
        return list;
    }

四、后序遍历的非递归写法

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

后序遍历相对于前面两个遍历会更难一些，后续遍历是左右根的顺序，仍然需要左子树走到底，然后回到根节点，这时需要判断右子树不为空的情况下这个右子树有没有被我们访问到，所以引入prev遍历，prev表示上一个完全被处理过得结点（循环开始之前为空）当node.right==null || node.right!=prev时，以node为跟的右子树已经完全被处理就可以放心的弹出node，将它的val添加到list。

排除树为空之后进入循环和中序遍历一样将树向做走到头并且入栈。

 这时出栈并且存储为node，然后判断node.right==null||node.right!=prev，并不满足说明他的右子树不为空并且还没有被处理，所以将node再次入栈，然后访问右子树node = node.right。

 然后再次进入循环，还是先一直向左走。

 然后出栈并且存储为node，这时node.right为空，所以直接添加其val到list中，使prev = node并且使node = null。

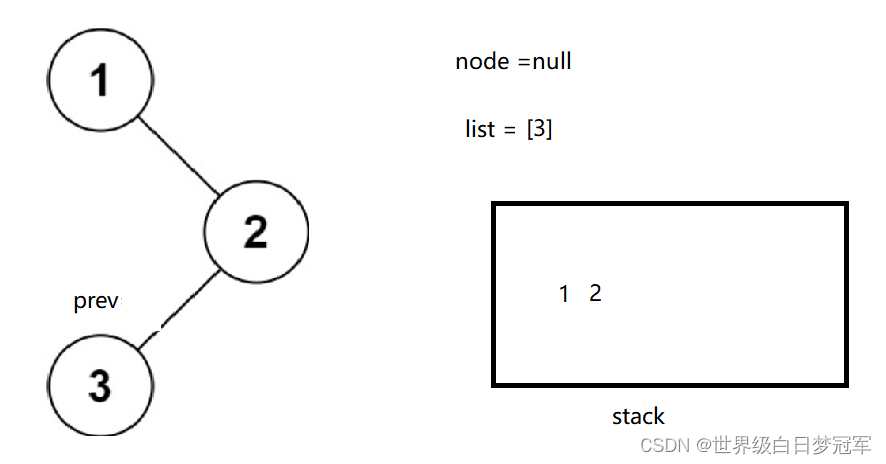
 然后再进入循环，出栈并且存储为node，它的node.right仍为空，所以list.add(node.val);prev = node;node = null;

  然后再进入循环，出栈并且存储为node，它的node.right==prev，所以list.add(node.val);prev = node;node = null;到这儿栈为空并且node==null所以循环结束，返回list。

    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root==null){
            return list;
        }
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode node = root;
        TreeNode prev = null;
        while (node!=null||!stack.isEmpty()){
            while (node!=null){
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            if(node.right==null||node.right==prev){
                list.add(node.val);
                prev = node;
                node = null;
            }else{
                stack.push(node);
                node = node.right;
            }
        }
        return list;
    }