🎉🎉🎉点进来你就是我的人了
博主主页:🙈🙈🙈戳一戳,欢迎大佬指点!
人生格言:当你的才华撑不起你的野心的时候,你就应该静下心来学习!欢迎志同道合的朋友一起加油喔🦾🦾🦾
目标梦想:进大厂,立志成为一个牛掰的Java程序猿,虽然现在还是一个🐒嘿嘿
谢谢你这么帅气美丽还给我点赞!比个心
目录
1.优先级队列和堆的概念
2. 向下调整算法
3.向上调整算法
4.向上调整算法和向下调整算法的建堆时间复杂度
1.向上调整算法建堆:
2.向下调整算法建堆:
5.优先级队列的实现
5.2插入数据
5.3删除数据
5.4获取堆顶元素
1.优先级队列和堆的概念
1.1.什么是优先级队列?
我们都学过队列,队列是一种先进先出的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,这就是优先级队列。比如有时候我们在打游戏的时候,别人打电话给你,那么系统一定是先处理打进来的电话。
1.2.什么是堆?
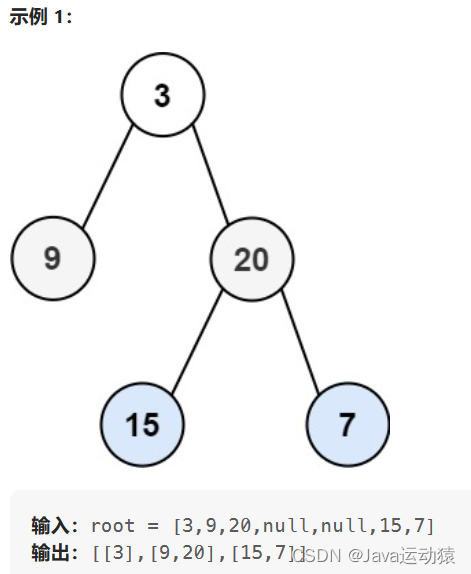
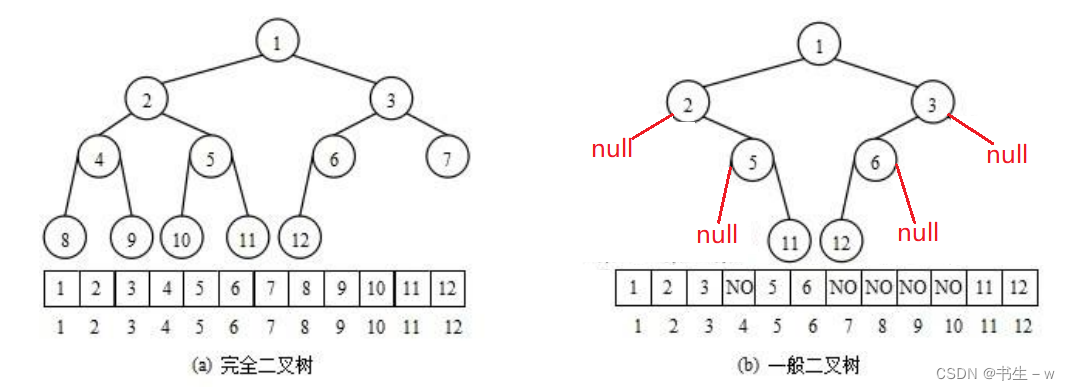
堆是一个(特殊的)完全二叉树,每个父节点都不大于或者不小于自己的孩子节点,层序遍历这个二叉树,顺序的放入一个数组中,这就是堆的存储。从逻辑上来说,堆是一棵完全二叉树,从存储底层来说,堆底层是一个数组。按种类分,它又分为大根堆和小根堆,请看下图:
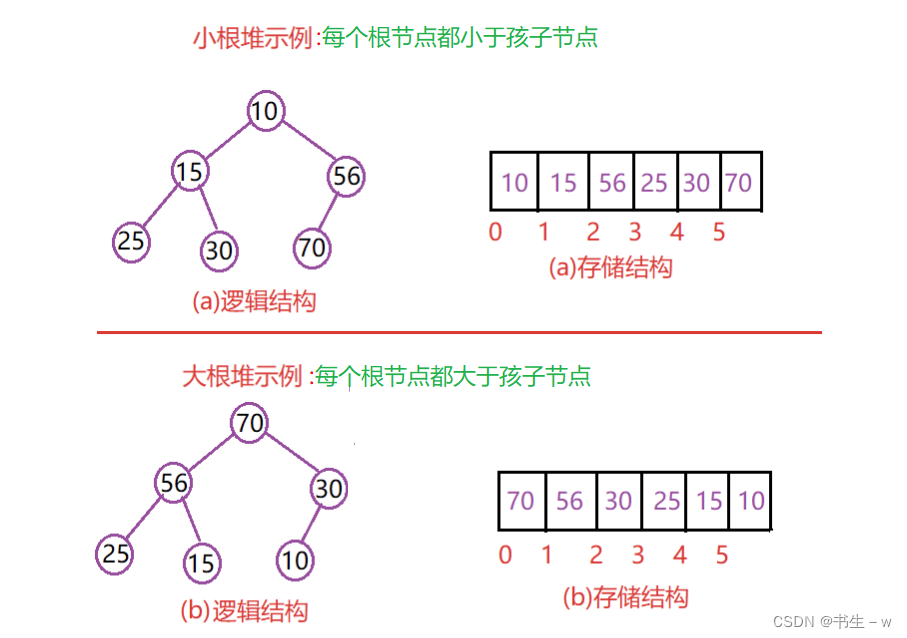
将元素存储到数组后,在以实现树的方式对堆进行实现。
设 i 结点为数组中的下标,则有以下特点:
- 如果 i 为0,则 i 表示的结点为根节点,否则 i 结点的双亲结点为(i - 1)/ 2;
- 如果 2 * i + 1 小于结点个数,则节点 i 的左孩子下标为 2 * i + 1,否则没有左孩子;
- 如果 2 * i + 2 小于结点个数,则节点 i 的左孩子下标为 2 * i + 2,否则没有右孩子。
注意:堆是一棵完全二叉树,它有着层序遍历的规则,所以采用顺序存储的方式来提高效率,而非完全二叉树是不适合使用顺序存储的方式来进行存储的,因为它为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
2. 向下调整算法
向下调整算法(Heapify Down)是一种用于维护堆(最大堆或最小堆)性质的算法。当堆中的某个节点的值不满足堆性质(在最大堆中,每个节点的值都应大于或等于其子节点的值;在最小堆中,每个节点的值都应小于或等于其子节点的值)时,向下调整算法会将该节点向下移动,直到它满足堆性质。
向下调整算法通常用于以下场景:
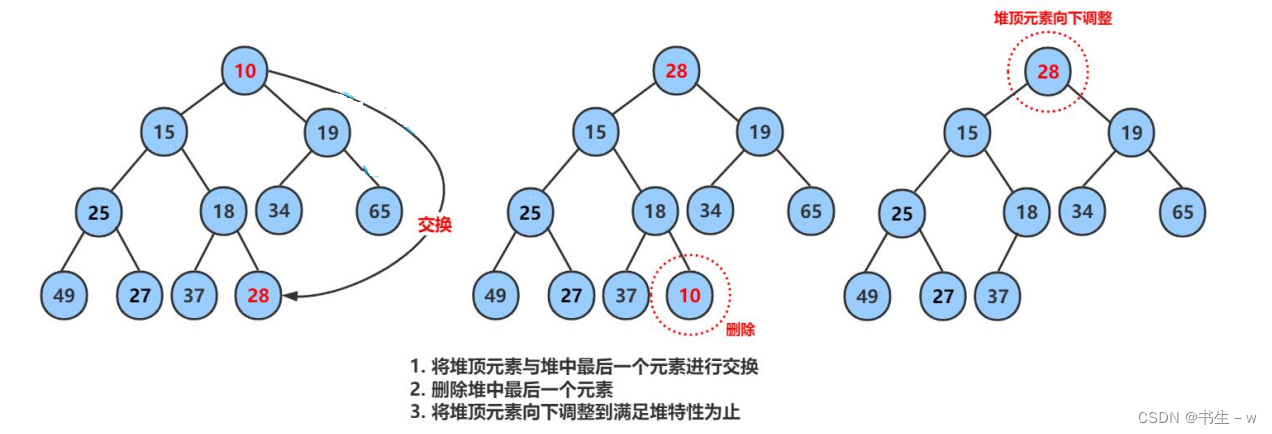
- 当从堆中删除最大值(最大堆)或最小值(最小堆)时,通常将堆的最后一个元素移动到堆顶,然后进行向下调整,以重新满足堆的性质。
- 当初始化一个堆时,可以自底向上地对所有非叶子节点进行向下调整,以构建一个有效的堆结构。
向下调整算法的过程如下:
- 从不满足堆性质的节点开始,找到其子节点中的最大值(最大堆)或最小值(最小堆)。
- 如果当前节点的值小于(最大堆)或大于(最小堆)子节点中的最大值或最小值,则将当前节点与该子节点交换。
- 重复以上过程,直到当前节点满足堆的性质,或已经到达堆的底部。
图示:
这种算法通过不断地将不满足堆性质的节点向下移动,直到找到合适的位置,从而维护了堆的性质。注意,向下调整算法在最坏情况下的时间复杂度为O(logn),其中n是堆中元素的数量。
3.向上调整算法
向上调整算法(Heapify Up)是一种用于维护堆(最大堆或最小堆)性质的算法。当堆中的某个节点的值不满足堆性质(在最大堆中,每个节点的值都应大于或等于其子节点的值;在最小堆中,每个节点的值都应小于或等于其子节点的值)时,向上调整算法会将该节点向上移动,直到它满足堆性质。
向上调整算法通常用于以下场景:
- 当向堆中插入一个新元素时,通常将该元素添加到堆的末尾,然后进行向上调整,以重新满足堆的性质。
向上调整算法的过程如下:
- 从不满足堆性质的节点开始,找到其父节点。
- 如果当前节点的值大于(最大堆)或小于(最小堆)其父节点的值,则将当前节点与其父节点交换。
- 重复以上过程,直到当前节点满足堆的性质,或已经到达堆的顶部。
这种算法通过不断地将不满足堆性质的节点向上移动,直到找到合适的位置,从而维护了堆的性质。注意,向上调整算法在最坏情况下的时间复杂度为O(logn),其中n是堆中元素的数量。
向上调整算法(Heapify Up)和向下调整算法(Heapify Down)都可以用于建堆,它们的时间复杂度有所不同。
4.向上调整算法和向下调整算法的建堆时间复杂度
1.向上调整算法建堆:
向上调整算法建堆的过程是从一个空堆开始,依次将数组中的元素插入堆中。对于每个插入的元素,执行向上调整。在这个过程中,每个元素的向上调整最多需要O(logn)时间(其中n是堆中元素的数量),因为堆的高度是logn。
为什么向下调整算法建堆的时间复杂度为O(logn)?
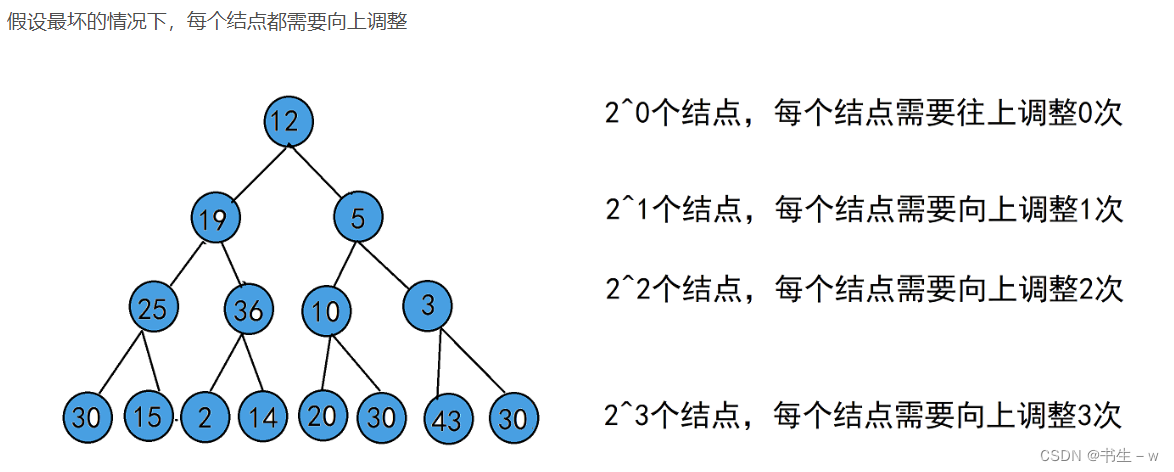
由二叉树的性质可以得知,每层结点的个数是2^(h-1),在第几层的结点如果需要调整的话,最多需要向上调整h-1次。那么,调整次数将与高度相关,如下
因此,向上调整算法建堆的总时间复杂度为O(nlogn)。这是因为我们需要对n个元素执行向上调整操作,每个操作的时间复杂度为O(logn)。
2.向下调整算法建堆:
向下调整算法建堆的过程是自底向上地对所有非叶子节点进行向下调整。从最后一个非叶子节点开始,依次向前遍历,对每个节点进行向下调整。这种方法的时间复杂度为O(n)。
为什么向下调整算法建堆的时间复杂度为O(n)?
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果)
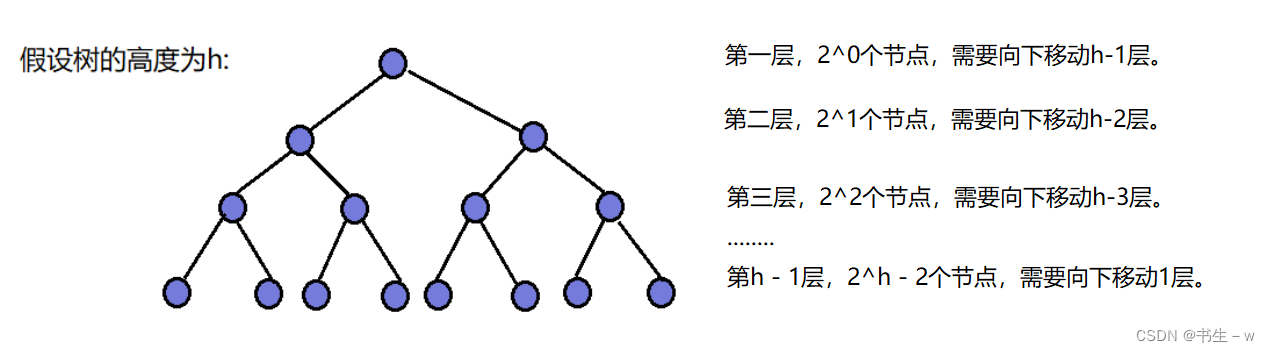

综上所述,向上调整算法建堆的时间复杂度为O(nlogn),而向下调整算法建堆的时间复杂度为O(n)。在实际应用中,向下调整算法建堆通常比向上调整算法建堆更高效。
5.优先级队列的实现
5.1创建大根堆 (向下调整建堆)
public class TestHeap {
public int elem[];
public int usedSize;
public static int DEFAULT_SIZE = 10;
public TestHeap() {
this.elem = new int[DEFAULT_SIZE];
}
public int[] createHeap(int[] array) {
//准备数据
for (int i = 0; i < array.length; i++) {
this.elem[i] = array[i];
this.usedSize++;
}
//创建大根堆
for (int p = (this.usedSize - 1 - 1) / 2; p >= 0 ; p--) {
//向下调整
shiftDown(p, this.usedSize);
}
return this.elem;
}
private void shiftDown(int parent, int len) {
//左孩子
int child = 2 * parent + 1;
//每一次调整的结束条件 --> child < len
while(child < len) {
//child < len 保证了有右孩子再去比较,拿到左右孩子的最大值
if(child + 1 < len && this.elem[child] < this.elem[child + 1]) {
child++;
}
//如果孩子节点大于父节点就交换
if(this.elem[child] > this.elem[parent]){
swap(parent, child);
//继续判断它子树是否调整
parent = child;
child = 2 * parent + 1;
} else {
//无需调整就退出循环
break;
}
}
}
private void swap(int parent, int child) {
int tmp = this.elem[parent];
this.elem[parent] = this.elem[child];
this.elem[child] = tmp;
}
}- 思路

5.2插入数据
public void offerHeap(int val) {
if(isFull()) {
this.elem = Arrays.copyOf(this.elem, 2*this.elem.length);
}
//1.放在最后一个位置
this.elem[this.usedSize] = val;
//2.进行向上调整
shiftUp(usedSize);
//3.有效数据+1
this.usedSize++;
}
private void shiftUp(int child) {
//父节点
int parent = (child - 1) / 2;
while(child > 0) {
//如果新插入元素比父节点大就交换
if(this.elem[child] > this.elem[parent]) {
swap(child,parent);
//向上调整
child = parent;
parent = (child - 1) / 2;
} else {
break;
}
}
}
private boolean isFull() {
return this.usedSize == this.elem.length;
}- 思路
1.检查容量是否足够,不够的话需要扩容
2.将待插入的数据放在 usedSize 位置
3.从usedSize下标的数据向上调整
向上调整需要一个前提,就是当前的堆需要是大根堆(小根堆),我们以大根堆举例:
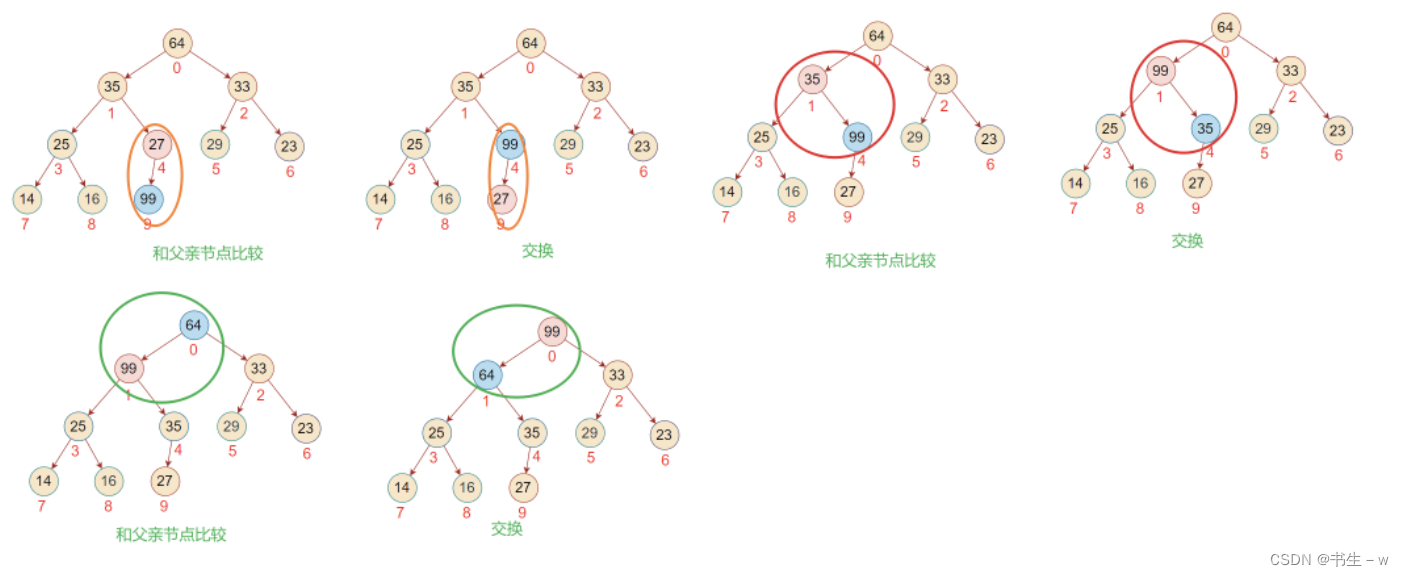
假如99这个结点是新插入的,需要将该树的结构重新改为大根堆,那么需要进行向上调整,具体过程就是:依次从下往上跟它的父节点比较,如果大于父节点则交换
可能会有人问不需要与左右孩子结点比较吗?
答案:不需要,因为在插入之前,该树就是一个大根堆,它的所有孩子节点都小于父节点,我们只需要修复新元素与其父节点之间的关系即可.
5.3删除数据
public int pollHeap() {
if(isEmpty()) {
throw new MyHeapIsEmptyException("优先级队列为空!");
}
int tmp = this.elem[0];
//将最后一个数据与堆顶数据进行交换
swap(usedSize-1,0);
this.usedSize--;
//向下调整
shiftDown(0, this.usedSize);
return tmp;
}
private boolean isEmpty() {
return this.usedSize == 0;
}- 思路
出堆,出的是堆顶元素,即下标为0处的元素,因为对于数组来说,头删是十分不利的,因此我们这里学要借助一个小技巧:1.将最后一个数据与堆顶数据进行交换
3.将堆中有效数据个数减少一个
2.然后再进行向下调整
5.4获取堆顶元素
public int peekHeap() {
if(isEmpty()) {
throw new MyHeapIsEmptyException("优先级队列为空!");
}
return this.elem[0];
}