引言

这篇论文可以说是对DeepWalk的扩展，按照LINE的说法，DeepWalk只捕捉了节点间的二阶相似性。LINE同时捕捉节点间的一阶相似性和二阶相似性。而Node2Vec同时也是同时捕捉一阶相似性和二阶相似性。和LINE不同的是，Node2Vec是基于Random Walk实现的。
首先介绍两个重要概念：

一阶相似性：在Node2vec中也叫做同质性，一阶相似性捕捉的是图中实际存在的结构。比如两个节点由一条边相连。则这两个节点应该具有相似性表示，按照Node2vec中的设计**，高度互联且属于相似网络的集群或社区的节点表示应该比较相近的，一阶相似性往往可以通过节点的DFS遍历得到**。
二阶相似性：在Node2vec中，也叫做结构的对等性。在网络中具有相似的结构节点表示应该相近。其并不强调两个节点是否在图中存在连接。即使两个节点离得很远，但是，由于结构上相似（连接得邻居结点相似）它们得表示也应该相似，所以二阶相似性可以发现不同得社区，二阶相似性可以通过结点得BFS遍历得到。
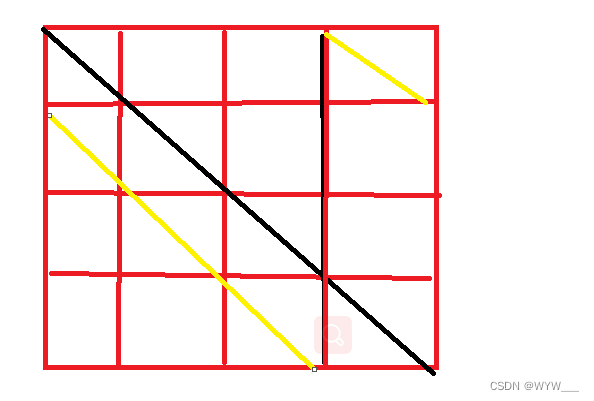
一阶相似性和二阶相似性的区别可以由下图看出：

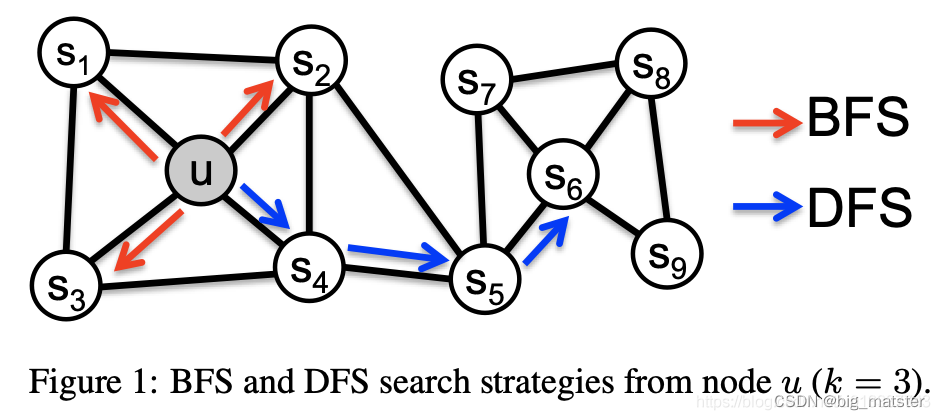
其中结点 $U$ 和结点 $S_6$ 就是属于二阶相似性，可由BFS遍历捕获到， $U$ 和 $S_1$ 都属于一阶相似性。可以由DFS捕获到。
注：这里的结论可能与我们的理解相反，即一戒嗔相似性不应该由BFS得到吗？下面介绍Node2Vec时候给出一些想法。
Node2Vec首先借鉴了自然语言处理的Skip-gram算法。给定一个节点，最大化周围邻近节点出现的条件概率。
$max_f\sum_{u \in V}logPr(N_s(u)|f(u))$

注意：这里的 $N_s(u)是节点u的邻居节点$ ，在Node2vec中，邻居节点有着不一样的定义，其不一定是由直接边相连的节点。而是根据采样策略确定的，后面会有详细的介绍。

为了方便优化上式，作者做了两个假设：

条件独立性假设：即各个邻居节点是相互独立的，所以有::
$Pr(N_s(u)|f(u)) = \prod_{n_i\in N_s(u)}Pr(n_i|f(u))$

特征空间对称性：即一个节点与它们之间的邻居节点影响是互相的，于是其可以对邻居节点进行嵌入表示。然后利用点乘形式刻画条件概率：
在这里插入图片描述
有了以上两个形式假设，可以把公式一改写为如下形式：

其中：

这里我们发现，最终导出的目标函数和LINE中的二阶相似性公式很想，实际上两者只相差了一个边的权重 $w_{ij}$ 和LINE中一样，计算 $Z_U$ 是耗时的，所以作者也采用了负采样的方法。

注意：LINE中对二阶相似性建模公式为：
在这里插入图片描述
写到这里可以发现，以上思想和Deepwalk非常相似，都是给定一个节点，最大化邻居节点（一次采样路径上的节点）出现的条件概率。只不过由于计算方式的不同，Node2vec捕捉了二阶相似性。Deepwalk捕捉了一阶相似性。Deepwalk到这里和新算法其实已经结束了。其接下来在介绍如何利用Hierarchical Softmax来优化条件概率的计算。而Node2vec到这里才刚刚开始，其和Deppwalk最大的不同是，如何采样节点，即采样邻居节点 $N_s(u)$

采样算法

传统的采样算法

传统的采样算法主要分为以下两部分：

基于BFS：基于广度优先遍历采样，那么通常 $N_s(u)$ 为节点u的直接邻居。即与 $u$ 直接相连接的节点。比如在图1中，我们设置采样大小 $K = 3$ ,那么 $N_s(u)$ 为 $s_1,s_2,s_3$ .
基于DFS：基于深度优先遍历的采样，那么采样节点会离原节点越来越来越元。比如在图1中，我们设置采样大小 $K = 3$ ,那么 $N_s(u)$ 为 $S_4,S_5.S_6$ .

实际上这两种比较极端的采样方法，DFS和BFS对于前面所说二阶相似性和二阶相似性。也叫同质和结构对等性。
node2vevv都是想通过设计一种采样算法，来融合一阶相似性和二阶相似性。

Node2vec中的采样算法

node2vec中的采样算法基于random walk的，给定源节点 $u$ ,采样长度为1.假设当前节点在 $C_{i - 1}$ 个采样的节点，那么下一个采样节点为 $x$ 的概率为:
在这里插入图片描述
其中 $\pi_{vx}$ 为从节点 $v$ 到节点 $x$ 的转移概率。Z为归一化常数。

传统的random walk 采样算法是完全随机的，这样就很难让采样过程自动一阶和二阶相似性。为此，作者提出了二阶随机游走。
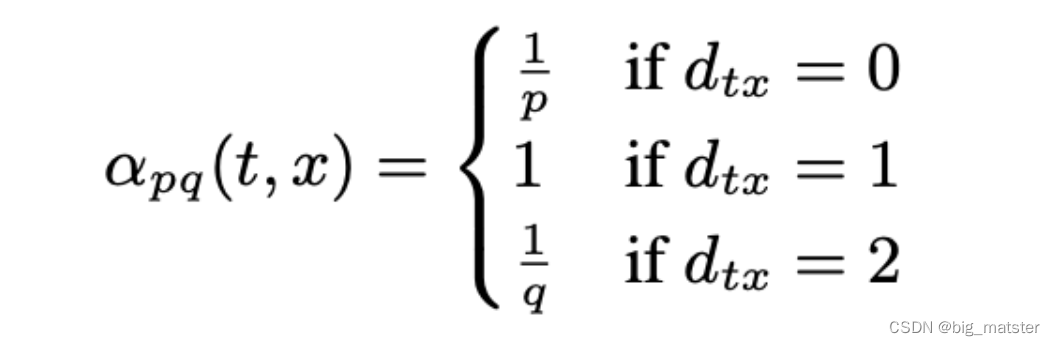
在这里插入图片描述

使用基于random walk采样的好处

在这里插入图片描述

node2vec的算法流程

在这里插入图片描述

特征学习算法

在这里插入图片描述

注意：node2vecwalk算法的第5步：采用了alas采样算法。可以在 $O (1)$ 的时间内完成。

实验

作者首先利用《悲惨世界》里的人物，共现关系验证了node2vec里的有效性，如下图所示：
在这里插入图片描述

总结

node2vec可以说是deepwalk的扩展，两个参数 $p 和 q$ 来控制， $b f s 和 d f s$ 两种方式的随机游走，而deepwalk是一个不加制约，漫无目的的游走。不能显式的建模节点之间的结构信息。

Alias sample采样算法

import numpy as np
def alias_setup(probs):
	'''
	Compute utility lists for non-uniform sampling from discrete distributions.
	Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/
	for details
	'''
	K = len(probs)
	q = np.zeros(K)    #保存样本概率
	J = np.zeros(K, dtype=np.int)  #保存补1的事件

	smaller = []
	larger = []
	for kk, prob in enumerate(probs):
	    q[kk] = K*prob
	    if q[kk] < 1.0:
	        smaller.append(kk)
	    else:
	        larger.append(kk)

	while len(smaller) > 0 and len(larger) > 0:
	    small = smaller.pop()
	    large = larger.pop()

	    J[small] = large
	    q[large] = q[large] + q[small] - 1.0  #q[large]-(1-q[small])
	    if q[large] < 1.0:
	        smaller.append(large)
	    else:
	        larger.append(large)

	return J, q    #（alias，prab）

def alias_draw(J, q):
	'''
	Draw sample from a non-uniform discrete distribution using alias sampling.
	'''
	K = len(J)

	kk = int(np.floor(np.random.rand()*K))
	if np.random.rand() < q[kk]:
	    return kk
	else:
	    return J[kk]

这部分为真正的源吗

import numpy as np
import networkx as nx
import random
from gensim.models import word2vec


class Graph():
    def __init__(self, nx_G, is_directed, p, q):
        self.G = nx_G
        self.is_directed = is_directed
        self.p = p
        self.q = q

    def node2vec_walk(self, walk_length, start_node):
        '''
        Simulate a random walk starting from start node.
        '''
        G = self.G
        alias_nodes = self.alias_nodes
        alias_edges = self.alias_edges

        walk = [start_node]

        while len(walk) < walk_length:
            cur = walk[-1]
            cur_nbrs = sorted(G.neighbors(cur))
            if len(cur_nbrs) > 0:
                # 如果序列中仅有一个结点，即第一次游走
                # alias_nodes中保存了alias_setup的[alias, accept]，通过alias_draw返回采样的下一个索引号
                if len(walk) == 1:
                    walk.append(cur_nbrs[alias_draw(alias_nodes[cur][0], alias_nodes[cur][1])])
                else:
                    # 当前游走结点的前一个结点和下一个节点
                    prev = walk[-2]
                    # 使用alias_edges中记录的[alias, accept]，来采样邻居中的下一个节点
                    next = cur_nbrs[alias_draw(alias_edges[(prev, cur)][0], 
                                                alias_edges[(prev, cur)][1])]
                    walk.append(next)
            else:
                break

        return walk

    def simulate_walks(self, num_walks, walk_length):
        '''
        Repeatedly simulate random walks from each node.
        '''
        G = self.G
        walks = []
        nodes = list(G.nodes())
		# nodes采样一次为一个epoch，此处就是num_walks个epoch
        print('Walk iteration:')
        for walk_iter in range(num_walks):
            print(str(walk_iter+1), '/', str(num_walks))
            random.shuffle(nodes)
            for node in nodes:
                walks.append(self.node2vec_walk(walk_length=walk_length, start_node=node))

        return walks

    def get_alias_edge(self, src, dst):
        '''
        Get the alias edge setup lists for a given edge.
        :return alias_setup(): 在上一次访问顶点 t ，当前访问顶点为 v 时到下一个顶点 x 的未归一化转移概率。
		:param src:  随机游走序列种的上一个结点
		:param dst:  当前结点
        参数p控制重复访问刚刚访问过的顶点的概率。若p较大，则访问刚刚访问过的顶点的概率会变低。
        参数q控制着游走是向外还是向内：
        若q>1，随机游走倾向于访问和上一次的t接近的顶点(偏向BFS)；若q<1，倾向于访问远离t的顶点(偏向DFS)
        '''
        G = self.G
        p = self.p
        q = self.q

        unnormalized_probs = []
        for dst_nbr in sorted(G.neighbors(dst)):
            if dst_nbr == src:   # 如果是要返回上一个节点
                unnormalized_probs.append(G[dst][dst_nbr]['weight']/p)
            elif G.has_edge(dst_nbr, src):   # 如果接下来访问的节点与src的距离与当前节点相等
                unnormalized_probs.append(G[dst][dst_nbr]['weight'])
            else:
                unnormalized_probs.append(G[dst][dst_nbr]['weight']/q)
        norm_const = sum(unnormalized_probs)
        normalized_probs =  [float(u_prob)/norm_const for u_prob in unnormalized_probs]

        return alias_setup(normalized_probs)

    def preprocess_transition_probs(self):
        '''
        Preprocessing of transition probabilities for guiding the random walks.
        用于引导随机游走的预处理，得到马尔可夫转移概率矩阵。
        '''
        G = self.G
        is_directed = self.is_directed

        alias_nodes = {}
        # G.neighbors(node) 与顶点相邻的所有顶点，更方便更快的访问adjacency字典用: G[cur]
        for node in G.nodes():
            # 根据邻居节点的权重，计算转移概率
            unnormalized_probs = [G[node][nbr]['weight'] for nbr in sorted(G.neighbors(node))]
            norm_const = sum(unnormalized_probs)
            # 计算当前节点到邻居节点的转移概率，其实就是权重归一化
            normalized_probs =  [float(u_prob)/norm_const for u_prob in unnormalized_probs]
            # 设置alias table，保存每个节点的accept[i]和alias[i]，为后面alias采样做准备。
            alias_nodes[node] = alias_setup(normalized_probs)

        alias_edges = {}
        triads = {}

        # 保存每条边的accept[i]和alias[i]
        if is_directed:
            for edge in G.edges():
                alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
        else:
            for edge in G.edges():
                alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])   # 随机游走序列种的上一个结点 当前节点
                alias_edges[(edge[1], edge[0])] = self.get_alias_edge(edge[1], edge[0])

        self.alias_nodes = alias_nodes
        self.alias_edges = alias_edges
        
        print(self.alias_nodes)
        print(self.alias_edges)
        return


def alias_setup(probs):
    '''
    Compute utility lists for non-uniform sampling from discrete distributions.
    Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/
    for details
    :param probs: 指定的采样结果概率分布列表。期望按这个概率列表来采样每个随机变量X。
    :return J: alias[i]表示第i列中不是事件i的另一个事件的编号。
    :return p: accept[i]表示事件i占第i列矩形的面积的比例。
    '''
    K = len(probs)
    # q表示：accept数组
    q = np.zeros(K)
    # J表示：alias数组
    J = np.zeros(K, dtype=np.int)

    # Alias方法将整个概率分布压成一个 1*N 的矩形，每个事件转换为矩形中的面积。
    # 将面积大于1的事件多出的面积补充到面积小于1对应的事件中，以确保每一个小方格的面积为1，
    # 同时，保证每一方格至多存储两个事件。
    smaller = [] # 面积小于1的事件
    larger = []  # 面积大于1的事件
    
    for kk, prob in enumerate(probs):
        q[kk] = K*prob
        if q[kk] < 1.0:
            smaller.append(kk)
        else:
            larger.append(kk)

    while len(smaller) > 0 and len(larger) > 0:
        small = smaller.pop()
        large = larger.pop()

        J[small] = large
        # 其实是 q[large] - (1.0 - q[small])，把大的削去(1.0 - q[small])填充到小的上
        q[large] = q[large] + q[small] - 1.0
		# 大的剩下的面积，放到下一轮继续倒腾
        if q[large] < 1.0:
            smaller.append(large)
        else:
            larger.append(large)

    return J, q

def alias_draw(J, q):
    '''
    Draw sample from a non-uniform discrete distribution using alias sampling.
    参考：https://zhuanlan.zhihu.com/p/54867139

    :param q: accept数组，表示事件i占第i列矩形的面积的比例；
    :param J: alias数组，表示alias矩形的第i列中不是事件i的另一个事件的编号，也就是填充的那一列的序号；
    生成一个随机数 kk in [0, K]，另一个随机数 x in [0,1],
    如果 x < accept[kk]，表示接受事件kk，返回kk，否则拒绝事件kk，返回alias[kk]
    '''
    K = len(J)

    kk = int(np.floor(np.random.rand()*K))
    if np.random.rand() < q[kk]:
        return kk
    else:
        return J[kk]
      
def read_graph(input_file, directed):
    '''
    Reads the input network in networkx.
    '''
    if directed:
        G = nx.read_edgelist(input_file, delimiter=",", nodetype=int, data=(('weight',float),), create_using=nx.DiGraph())
    else:
        G = nx.read_edgelist(input_file, delimiter=",", nodetype=int, create_using=nx.DiGraph())
        for edge in G.edges():
            G[edge[0]][edge[1]]['weight'] = 1

    if not directed:
        G = G.to_undirected()

    return G

def learn_embeddings(walks):
    '''
    Learn embeddings by optimizing the Skipgram objective using SGD.
    '''
    walks = [list(map(str, walk)) for walk in walks]
    print(walks)
#     model = word2vec.Word2Vec(walks, vector_size=64, window=3, min_count=0, sg=1, workers=1, epochs=5)
    # model.save_word2vec_format(args.output)
    #model.wv.save_word2vec_format(args.output, binary=False)
    
    return

def main(directed):
    '''
    Pipeline for representational learning for all nodes in a graph.
    '''
    nx_G = read_graph(r"C:\Users\Administrator\TensorFlow\game.csv", directed)
    print(list(nx_G.edges(data=True)), list(nx_G))
    for node in nx_G.neighbors(2):
        print(node)
    G = Graph(nx_G, False, 1, 2)
    
    G.preprocess_transition_probs()
    walks = G.simulate_walks(5, 3)
    learn_embeddings(walks)

if __name__ == "__main__":
    main(directed = False)